Содержание
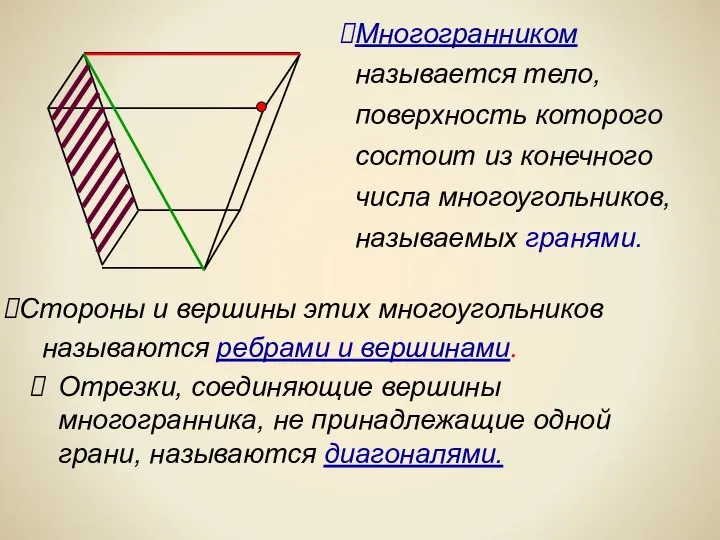
- 2. Отрезки, соединяющие вершины многогранника, не принадлежащие одной грани, называются диагоналями. Многогранником называется тело, поверхность которого состоит
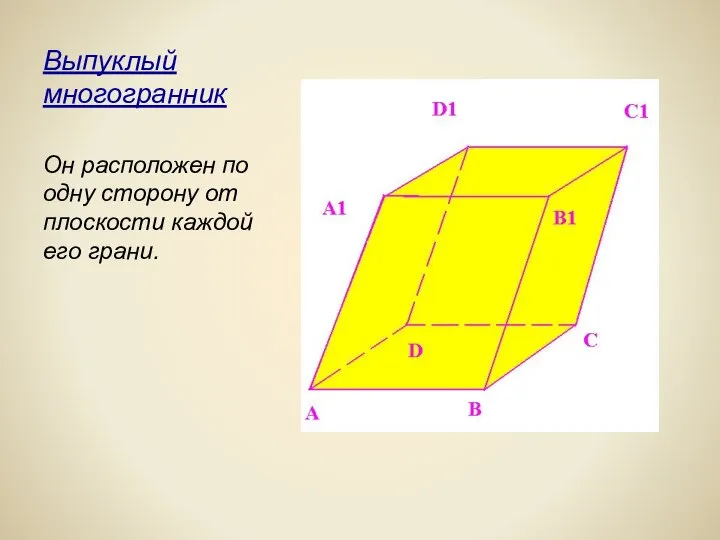
- 3. Выпуклый многогранник Он расположен по одну сторону от плоскости каждой его грани.
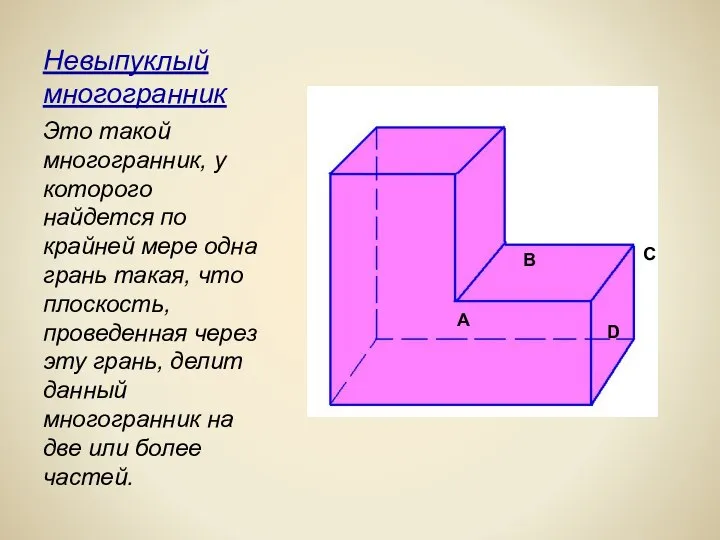
- 4. Невыпуклый многогранник Это такой многогранник, у которого найдется по крайней мере одна грань такая, что плоскость,
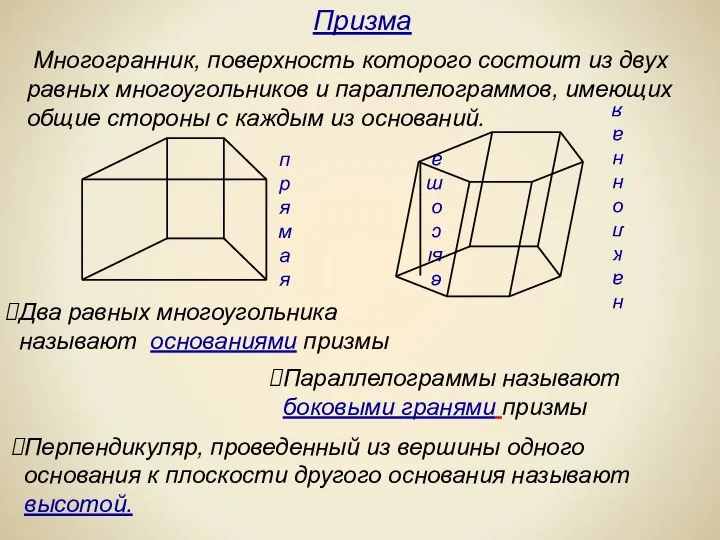
- 5. Многогранник, поверхность которого состоит из двух равных многоугольников и параллелограммов, имеющих общие стороны с каждым из
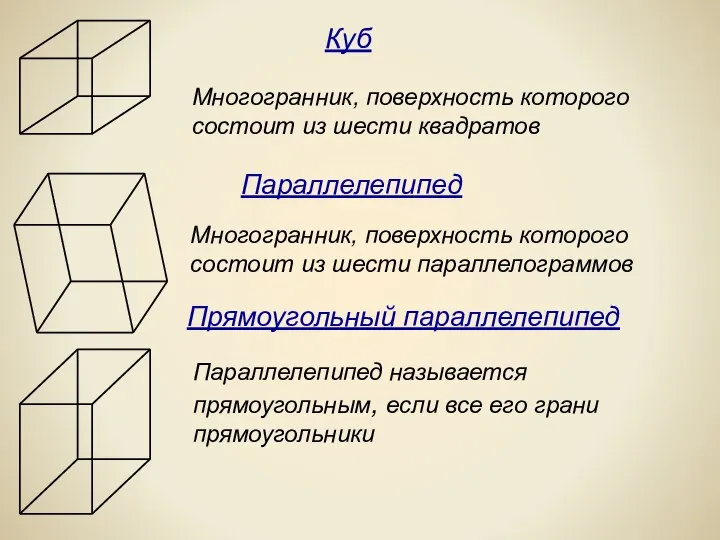
- 6. Многогранник, поверхность которого состоит из шести квадратов Многогранник, поверхность которого состоит из шести параллелограммов Параллелепипед называется
- 7. Площадь призмы Sбок. + 2Sосн Sбок. = Ph a b h Теорема: Площадь боковой поверхности прямой
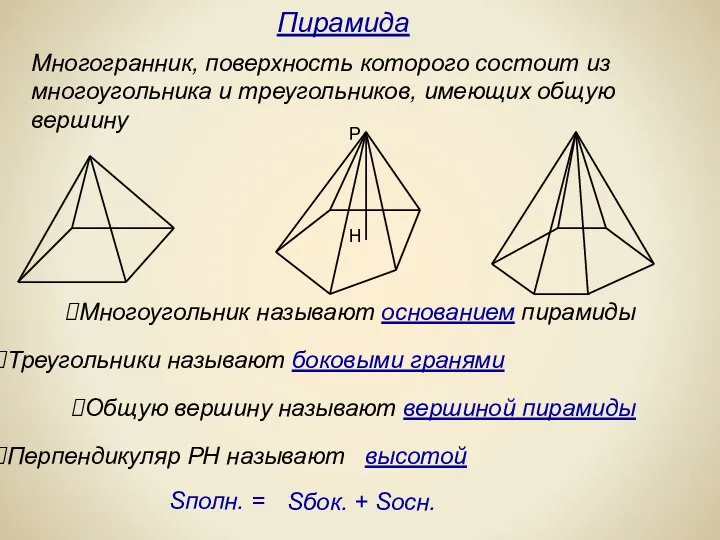
- 8. Многогранник, поверхность которого состоит из многоугольника и треугольников, имеющих общую вершину Многоугольник называют основанием пирамиды Треугольники
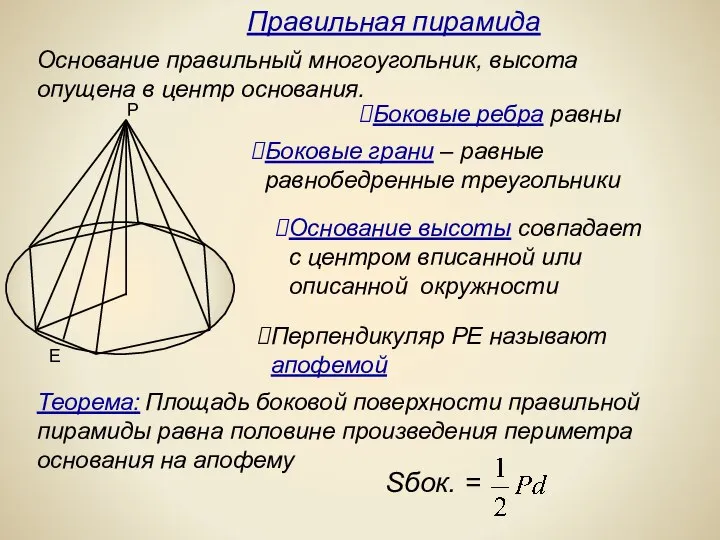
- 9. Основание правильный многоугольник, высота опущена в центр основания. Перпендикуляр РЕ называют апофемой Теорема: Площадь боковой поверхности
- 10. Усеченная пирамида Боковые грани – трапеции Теорема: Площадь боковой поверхности правильной усеченной пирамиды равна половине произведения
- 11. Выпуклый многогранник называется правильным, если все его грани - равные правильные многоугольники и в каждой его
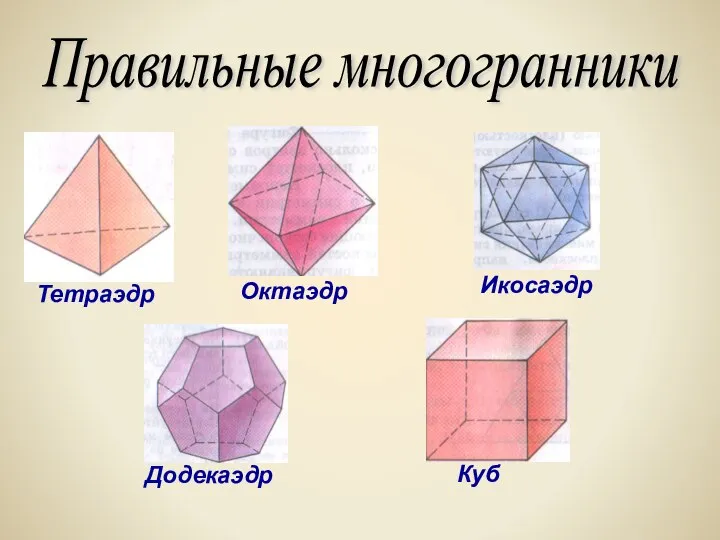
- 12. Правильные многогранники
- 13. Названия этих многогранников пришли из Древней Греции, и в них указывается число граней: «эдра» - грань
- 14. Теорема Эйлера Число граней + число вершин - число ребер = 2. 4 4 6 8
- 16. Скачать презентацию





 Математические модели и методы
Математические модели и методы Теорема о точке пересечения высот треугольника
Теорема о точке пересечения высот треугольника Модель конфликта
Модель конфликта ЛОГАРИФМ. Свойства логарифма.
ЛОГАРИФМ. Свойства логарифма. Прямоугольник. Ромб. Квадрат
Прямоугольник. Ромб. Квадрат Подготовка к контрольной работе
Подготовка к контрольной работе Решаем со Смешариками
Решаем со Смешариками Одночлены и многочлены
Одночлены и многочлены Комбинаторика
Комбинаторика Арифметическая прогрессия (9 класс)
Арифметическая прогрессия (9 класс) Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам)
Соотношение между сторонами и углами прямоугольного треугольника (задачи по готовым чертежам)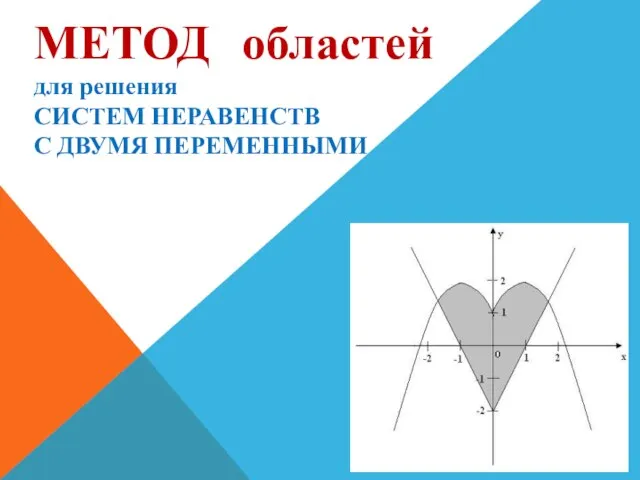 Метод областей для решения систем неравенств с двумя переменными
Метод областей для решения систем неравенств с двумя переменными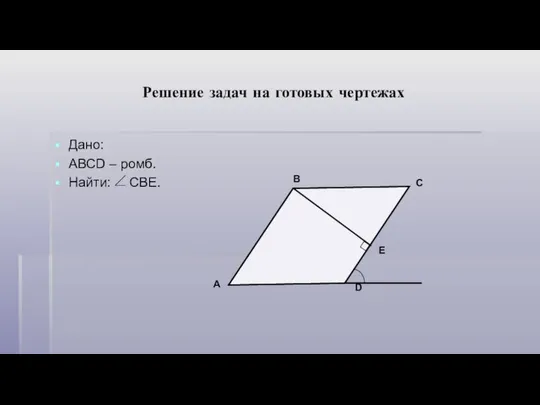 Решение задач на готовых чертежах 8 класс
Решение задач на готовых чертежах 8 класс Викторина. Первый тур
Викторина. Первый тур Последний герой
Последний герой Подготовка к ГИА по математике
Подготовка к ГИА по математике Первообразная функции. Неопределенный интеграл
Первообразная функции. Неопределенный интеграл Основы логики
Основы логики Решение уравнения cosx = a. Понятие арккосинуса числа
Решение уравнения cosx = a. Понятие арккосинуса числа Математическая шифровка
Математическая шифровка Математические станции
Математические станции Тема: Деление десятичных дробей на натуральные числа. Цель урока: закрепить навыки деления десятичной дроби на натуральное число
Тема: Деление десятичных дробей на натуральные числа. Цель урока: закрепить навыки деления десятичной дроби на натуральное число Движение в пространстве
Движение в пространстве Дробно-рациональные уравнения. Применение при решении задач
Дробно-рациональные уравнения. Применение при решении задач Векторы. Геометрия (9 класс)
Векторы. Геометрия (9 класс) Элективный курс. Алгебра 11 класс
Элективный курс. Алгебра 11 класс Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств Муниципальное казенное общеобразовательное учреждение Сайдыпская основная общеобразовательная школа. Устный счет на уроках ма
Муниципальное казенное общеобразовательное учреждение Сайдыпская основная общеобразовательная школа. Устный счет на уроках ма