Содержание
- 2. 1.1. Первообразная функция ОПР. Функция называется первообразной для функции на данном промежутке (a;b), если для любого
- 3. Теорема 1.1. Если функция f(x) непрерывна на данном интервале, то на этом интервале она имеет первообразную.
- 4. где – произвольная постоянная. ОПР. Совокупность всех первообразных для данной функции называется ее неопределенным интегралом и
- 5. Знак называется интегралом, функция – подынтегральной функцией, – подынтегральным выражением, Операция нахождения неопределенного интеграла для данной
- 6. 1. Дифференциал от неопределенного интеграла равен подынтегральному выражению: Основные свойства неопределенного интеграла
- 7. 2. Производная неопределенного интеграла равна подынтегральной функции: Таким образом, правильность интегрирования проверяется дифференцированием!
- 8. 3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
- 9. 4. Постоянный множитель можно выносить за знак интеграла:
- 10. 5. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых
- 11. 6. Если то где − произвольная функция, имеющая непрерывную производную. Данное свойство называется инвариантностью неопределенного интеграла.
- 12. При вычислении неопределенного интеграла используют формулу:
- 13. Таблица простейших интегралов
- 15. Вычисление интегралов с помощью преобразования подынтегрального выражения к табличной форме и использования свойств неопределенного интеграла называется
- 16. Пример 1. Используя таблицу и свойства интегралов, найти интегралы.
- 19. Непосредственное интегрирование Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и
- 20. При сведении данного интеграла к табличному часто используется следующее преобразование дифференциала (операция «подведения под знак дифференциала»).
- 21. Примеры
- 23. Метод замены переменной (метод подстановки) состоит в преобразовании интеграла в другой интеграл который вычисляется проще, чем
- 24. Пример
- 27. Интегрирование по частям Формула где и – дифференцируемые функции, называется формулой интегрирования по частям. Метод интегрирования
- 28. Некоторые типы интегралов, которые можно вычислять методом интегрирования по частям Интегралы вида где − многочлен, m
- 29. 2. Интегралы вида Здесь полагают за u обозначают остальные сомножители. 3. Интегралы вида где a и
- 31. Скачать презентацию






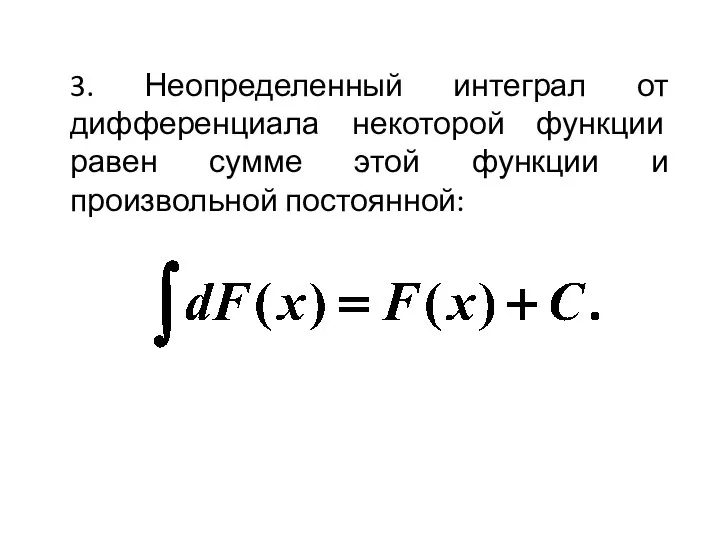





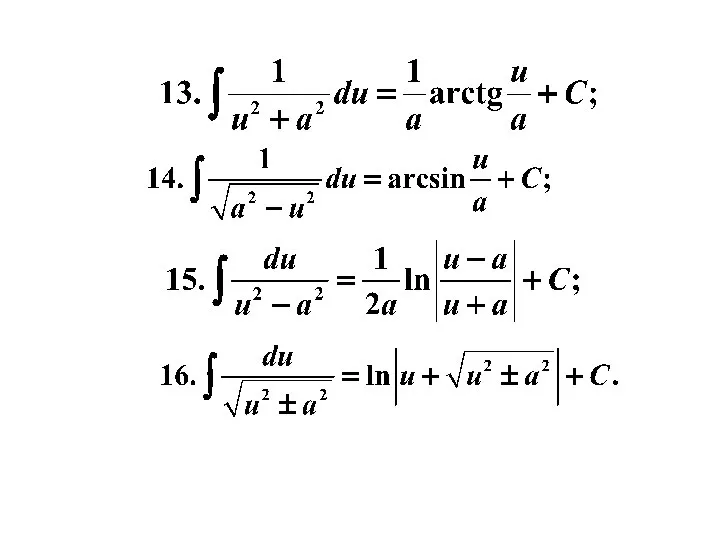


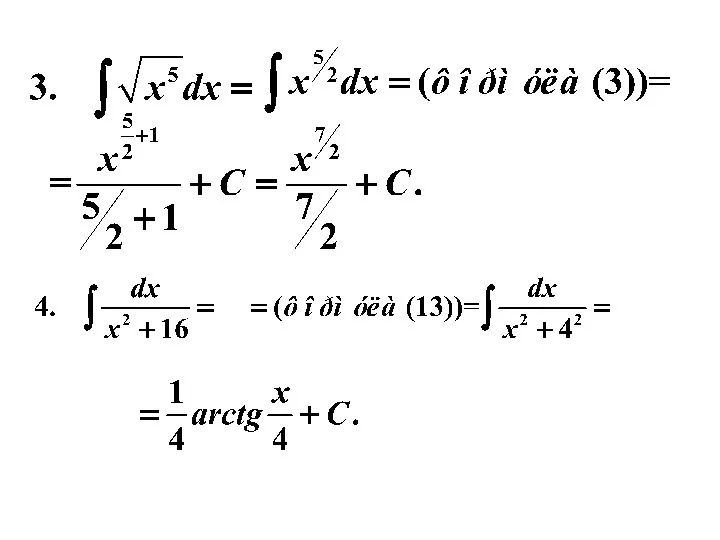
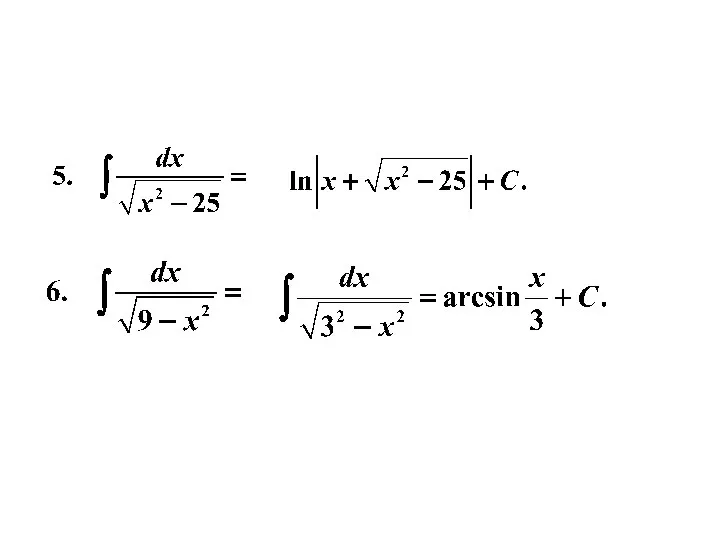


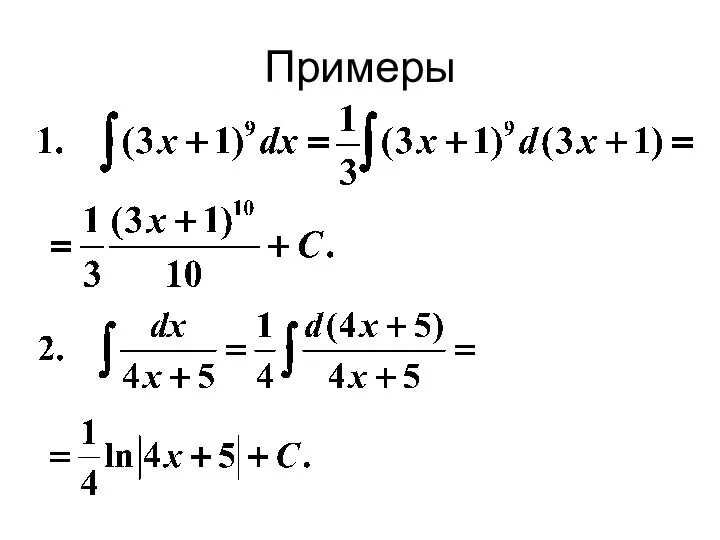




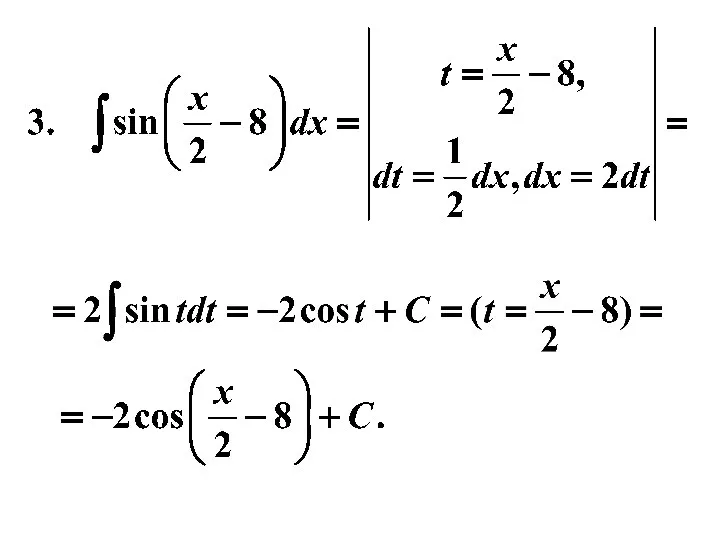



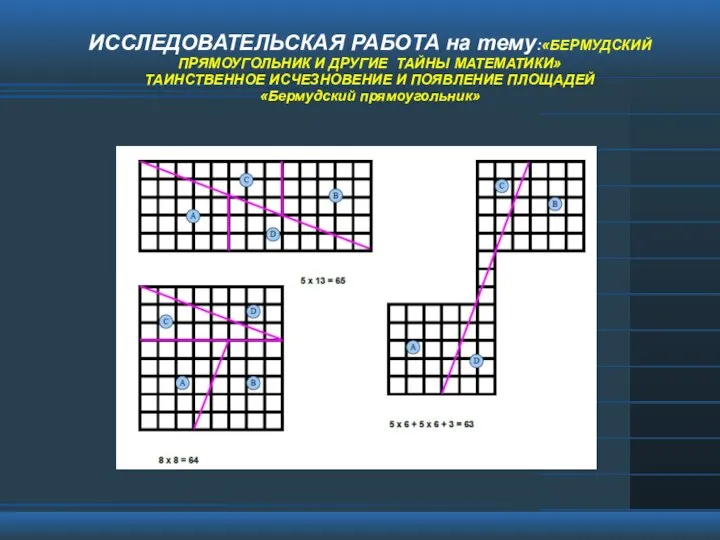 «Бермудский прямоугольник и другие тайны математики», таинственное исчезновение и появление площадей
«Бермудский прямоугольник и другие тайны математики», таинственное исчезновение и появление площадей Решение задач по теме «Четырехугольники» по готовым чертежам
Решение задач по теме «Четырехугольники» по готовым чертежам Пустыня ошибок
Пустыня ошибок Аттестацианная работа. Исследовательская работа. Фигурные числа
Аттестацианная работа. Исследовательская работа. Фигурные числа Сложение с переходом через десяток
Сложение с переходом через десяток Задачи на переливание жидкости
Задачи на переливание жидкости Сумма углов треугольника
Сумма углов треугольника Позиционные системы счисления, отличные от десятичной
Позиционные системы счисления, отличные от десятичной Уравнение плоскости, проходящей через три точки
Уравнение плоскости, проходящей через три точки Ehtimalın klassik tərifi
Ehtimalın klassik tərifi Производные элементарных функций
Производные элементарных функций Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспор
Транспортир Измерение углов Транспортир. История транспортира. Использование транспортира в жизни человека. Виды транспор Предел последовательности и предел функции
Предел последовательности и предел функции Счастливый случай. Интеллектуальная игра
Счастливый случай. Интеллектуальная игра СМО M/G/1/∞, СМО с многомерным входящим потоком, СМО с приоритетами. Характеристики СМО. (Лекция 5)
СМО M/G/1/∞, СМО с многомерным входящим потоком, СМО с приоритетами. Характеристики СМО. (Лекция 5) Числовые выражения Начальная школа XXI век
Числовые выражения Начальная школа XXI век Стандартный вид числа
Стандартный вид числа Решение простейших тригонометрических неравенств
Решение простейших тригонометрических неравенств Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Числовые ряды
Числовые ряды Тригонометрия (10 класс)
Тригонометрия (10 класс) Счет до 10
Счет до 10 Понятие вектора в пространстве
Понятие вектора в пространстве Округление чисел. 5 класс
Округление чисел. 5 класс МЕРЫ ИЗМЕРЕНИЯ МАССЫ
МЕРЫ ИЗМЕРЕНИЯ МАССЫ Исследование функций. 10 класс
Исследование функций. 10 класс Післяоптимізаційний аналіз задач лінійного програмування
Післяоптимізаційний аналіз задач лінійного програмування Пифагор и теоремы. Интересные факты из жизни Пифагора
Пифагор и теоремы. Интересные факты из жизни Пифагора