Содержание
- 2. Основные понятия Комплексным числом называется выражение вида где и – действительные числа, а – мнимая единица.
- 3. Два комплексных числа называются равными тогда и только тогда, когда Комплексное число равно 0 тогда и
- 4. Понятия «больше» и «меньше» для комплексных чисел не определяются. Два комплексных числа называются сопряженными. Справедливо равенство
- 5. Извлечение корней из комплексных чисел Корнем n-ой степени из комплексного числа называется комплексное число , удовлетворяющее
- 6. Пример Вычислить Решить уравнение Решить уравнение Решение. 1.
- 7. 2. 3.
- 8. Тема: ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ §1. Дифференциальные уравнения первого порядка
- 9. Дифференциальные уравнения первого порядка Уравнение связывающее независимую переменную x, искомую функцию y и ее производную y’,
- 10. Если дифференциальное уравнение можно записать в виде то говорят, что оно разрешимо относительно производной. Это уравнение
- 11. Решение дифференциального уравнения Решением (или интегралом) дифференциального уравнения первого порядка называется любая функция , которая при
- 12. Задача Коши Задача отыскания решения дифференциального уравнения, удовлетворяющего заданному начальному условию , называется задачей Коши. Задача
- 13. Общее решение ДУ Общим решением дифференциального уравнения называется такая функция где – C произвольная постоянная, что
- 14. Если общее решение записать в виде то это соотношение называется общим интегралом дифференциального уравнения. Частным решением
- 15. Дифференциальные уравнения с разделяющимися переменными Уравнение вида Где – заданные функции, называется дифференциальным уравнением с разделяющимися
- 16. Если то, разделив уравнение (1) на получим уравнение которое называется дифференциальным уравнением с разделенными переменными (коэффициент
- 17. Общий интеграл полученного уравнения находится почленным интегрированием: Уравнение Где – заданные функции, сводится к уравнению (2).
- 18. Схема решения ДУ с разделяющимися переменными
- 20. Линейные дифференциальные уравнения первого порядка Дифференциальное уравнение вида Где , , – непрерывные функции, называется линейным
- 21. §2. Дифференциальные уравнения второго порядка Уравнение вида или называется дифференциальным уравнением второго порядка. Начальные условия для
- 22. Решением уравнения называется всякая функция , которая при подстановке вместе с y’ и y’’ в это
- 23. Общим решением уравнения называется функция , зависящая от двух произвольных постоянных и и такая, что: 1)
- 24. Понижение порядка дифференциальных уравнений В некоторых частных случаях удается понизить порядок дифференциального уравнения второго порядка. В
- 25. Типы уравнений, допускающих понижение порядка Уравнение Способ понижения порядка
- 26. Пример Найти общее решение уравнения Решение. Интегрируя, получим – уравнение с разделяющимися переменными.
- 27. Так как разделяем переменные и интегрируем:
- 28. ИНТЕГРИРОВАНИЕ ДУ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ Уравнение вида (p и q – постоянные) называется линейным
- 29. Уравнение называется характеристическим для дифференциального уравнения Для составления характеристического уравнения в уравнении (4) заменяют Вид общего
- 30. Пример Составить характеристические уравнения для следующих дифференциальных уравнений: 1. 2. 3. 4.
- 33. Пример 1. Найти общее решение уравнения Решение. Составим характеристическое уравнение, заменяя в данном уравнении Получим
- 35. Скачать презентацию





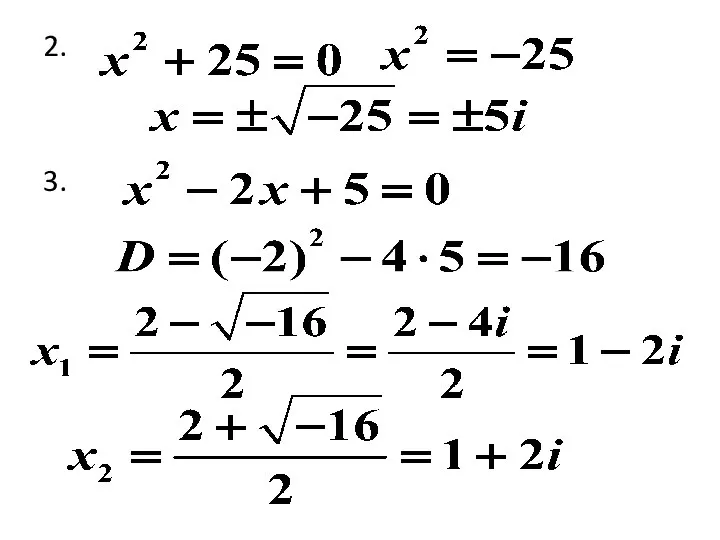



















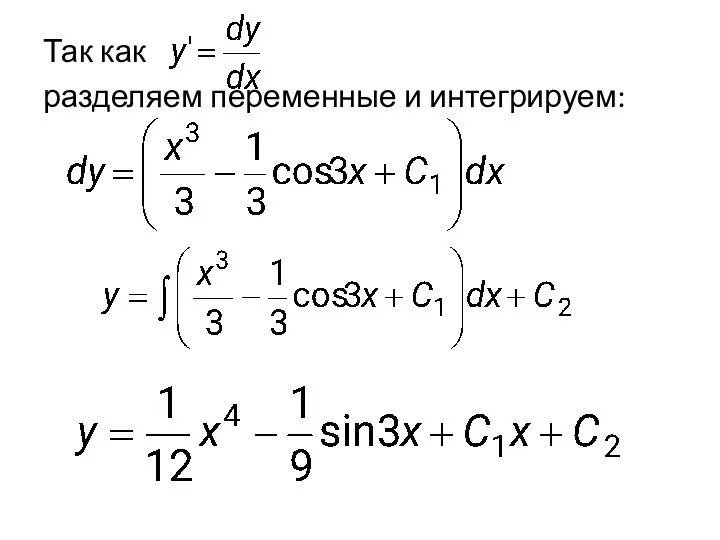






 Виды углов. Измерение углов
Виды углов. Измерение углов Прикладные задачи математики
Прикладные задачи математики Статистические оценки параметров распределения
Статистические оценки параметров распределения Решение уравнений
Решение уравнений Задачи математической статистики
Задачи математической статистики Урок математики в 3классе. «Путешествие по Астане» подготовила учитель начальных классов Пак Светлана Александровна
Урок математики в 3классе. «Путешествие по Астане» подготовила учитель начальных классов Пак Светлана Александровна  Окружности. Равносторонний треугольник:
Окружности. Равносторонний треугольник: Таблица умножения. Разминка
Таблица умножения. Разминка Арифметическая прогрессия. Формула n – го члена арифметической прогрессии
Арифметическая прогрессия. Формула n – го члена арифметической прогрессии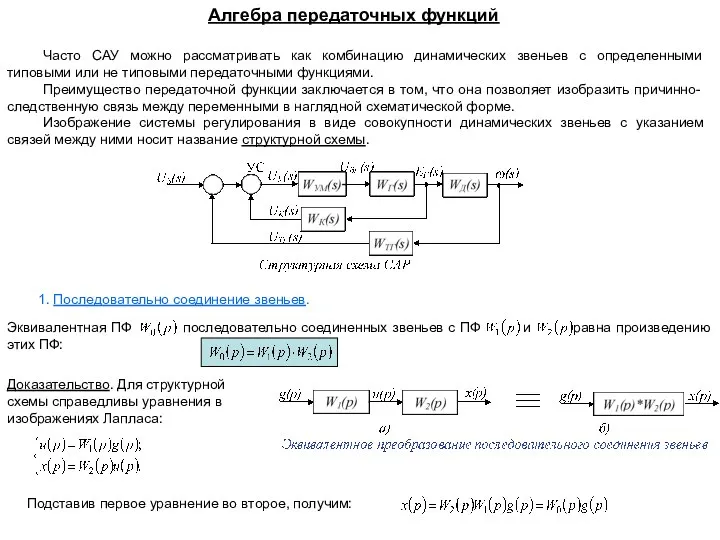 Алгебра передаточных функций
Алгебра передаточных функций הקדמה ,סוגי נורמות ומטריקות .טופולוגיה - תרגול 1
הקדמה ,סוגי נורמות ומטריקות .טופולוגיה - תרגול 1 مهارات التعامل مع اختبار القدرات
مهارات التعامل مع اختبار القدرات Рациональные числа
Рациональные числа Извлечение квадратных корней из больших чисел без калькулятора
Извлечение квадратных корней из больших чисел без калькулятора Modelagem Matemático Computacional FFI0321
Modelagem Matemático Computacional FFI0321 Деление на десятичную дробь
Деление на десятичную дробь Аттестационная работа. Подготовка к ОГЭ по математике
Аттестационная работа. Подготовка к ОГЭ по математике Функция у = sin x , её свойства и график
Функция у = sin x , её свойства и график Правильный многогранник
Правильный многогранник Умножение натуральных чисел
Умножение натуральных чисел Плоскость и прямая в пространстве
Плоскость и прямая в пространстве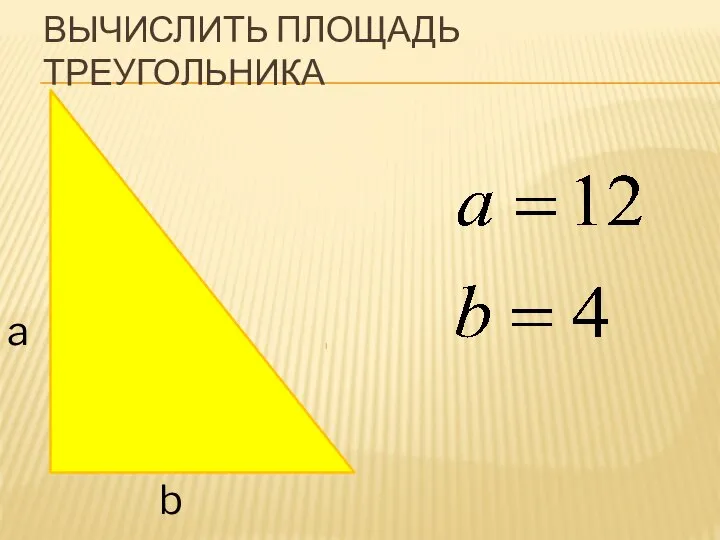 Вычисление площади треугольника
Вычисление площади треугольника Случайные процессы общего вида
Случайные процессы общего вида Презентация на тему Решение задач Магия тел вращения
Презентация на тему Решение задач Магия тел вращения  Линии
Линии Свойства делимости
Свойства делимости Уравнение плоскости
Уравнение плоскости Каскады из правильных многогранников
Каскады из правильных многогранников