Содержание
- 2. § 1. Неопределенный интеграл и его свойства Определение 1. Функция F(x) называется первообразной (для) функции f(x)
- 3. § 1. Неопределенный интеграл и его свойства 1. Определение неопределенного интеграла Определение 2. Совокупность всех первообразных
- 4. § 1. Неопределенный интеграл и его свойства 1. Определение неопределенного интеграла С геометрической точки зрения неопределенный
- 5. § 1. Неопределенный интеграл и его свойства 1.2. Свойства неопределенного интеграла 1. Благодаря этому свойству правильность
- 6. § 1. Неопределенный интеграл и его свойства 1.2. Свойства неопределенного интеграла 4. 5. Инвариантность формулы интегрирования.
- 7. § 1. Неопределенный интеграл и его свойства 1.2. Свойства неопределенного интеграла 6. Если подынтегральная функция f(x)
- 8. § 1. Неопределенный интеграл и его свойства 1.3. Таблица интегралов
- 9. § 1. Неопределенный интеграл и его свойства 1.3. Таблица интегралов Добавить к этой таблице еще несколько
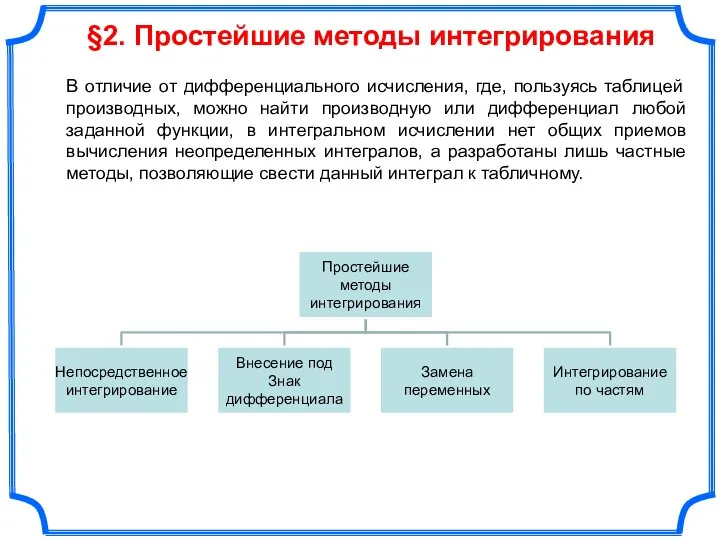
- 10. §2. Простейшие методы интегрирования В отличие от дифференциального исчисления, где, пользуясь таблицей производных, можно найти производную
- 11. §2. Простейшие методы интегрирования 2.1. Непосредственное интегрирование 1. 2. 3.
- 12. §2. Простейшие методы интегрирования 2.1. Непосредственное интегрирование 4. 5.
- 13. §2. Простейшие методы интегрирования 2.2. Подведение под знак дифференциала Данный метод опирается на свойство 5 неопределенного
- 14. §2. Простейшие методы интегрирования 2.2. Подведение под знак дифференциала 2. 1.
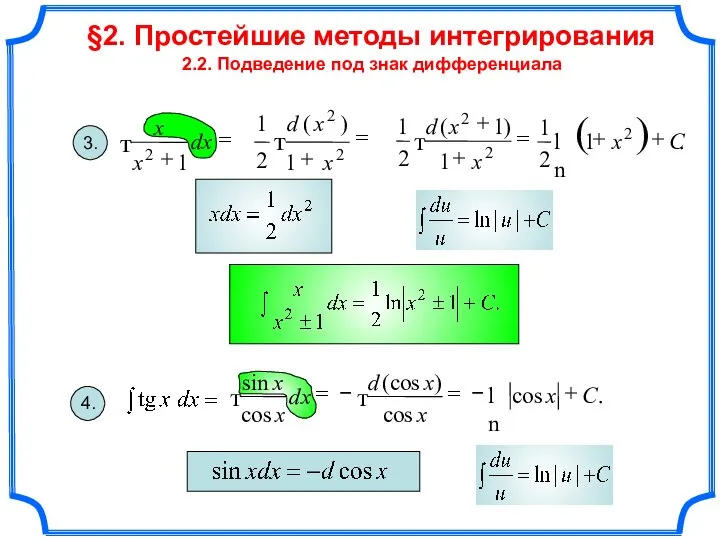
- 15. §2. Простейшие методы интегрирования 2.2. Подведение под знак дифференциала 3. т = + dx x x
- 16. §2. Простейшие методы интегрирования 2.2. Подведение под знак дифференциала 5. 6. 7.
- 17. §2. Простейшие методы интегрирования 2.3. Замена переменной в неопределенном интеграле Теорема. Пусть функция f(x) определена на
- 18. §2. Простейшие методы интегрирования 2.3. Замена переменной в неопределенном интеграле 1. 2.
- 19. §2. Простейшие методы интегрирования 2.3. Интегрирования по частям Теорема. Если функции u(x) и v(x) дифференцируемы на
- 20. §2. Простейшие методы интегрирования 2.3. Интегрирования по частям
- 21. §2. Простейшие методы интегрирования 2.3. Интегрирования по частям 1. 2. 3.
- 22. §2. Простейшие методы интегрирования 2.3. Интегрирования по частям 4.
- 23. §2. Простейшие методы интегрирования 2.3. Интегрирования по частям Рассмотрим так называемый возвратный интеграл: 5. Таким образом,
- 24. §2. Простейшие методы интегрирования 2.3. Интегрирования по частям Получим так называемую рекуррентную формулу для интеграла 6.
- 26. Скачать презентацию





















 Правильные многогранники
Правильные многогранники Порівняння виразу і числа. Складання задач за поданою схемою розв’язання
Порівняння виразу і числа. Складання задач за поданою схемою розв’язання Команда «Интеграл»
Команда «Интеграл» Задачи на совместную работу (урок 3)
Задачи на совместную работу (урок 3) Презентация по математике "Округление десятичных чисел" - скачать
Презентация по математике "Округление десятичных чисел" - скачать  Оценка точности на основе весов. Теория погрешностей измерений
Оценка точности на основе весов. Теория погрешностей измерений Успоредни линии. Триъгълници
Успоредни линии. Триъгълници Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Путешествие в сказочную страну
Путешествие в сказочную страну Случаи сложения и вычитания, основанные на знании нумерации чиселм
Случаи сложения и вычитания, основанные на знании нумерации чиселм Золотое сечение
Золотое сечение Презентация по математике "Число и цифра 9" - скачать бесплатно
Презентация по математике "Число и цифра 9" - скачать бесплатно Показательная функция, ее свойства и график
Показательная функция, ее свойства и график Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Системы счисления
Системы счисления Параллельные вычислительные процессы
Параллельные вычислительные процессы Задачи, составление и решение. Математический тренажер
Задачи, составление и решение. Математический тренажер Презентация на тему Взаимное расположение прямой и окружности
Презентация на тему Взаимное расположение прямой и окружности Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Презентация по математике "Круг Эйлера" - скачать
Презентация по математике "Круг Эйлера" - скачать  Математика на войне
Математика на войне Параллельные плоскости
Параллельные плоскости Счет в пределах 20. Подготовка к введению задач в два действия
Счет в пределах 20. Подготовка к введению задач в два действия Сравнение предметов по различным признакам
Сравнение предметов по различным признакам Аттестационная работа. Методическая разработка по выполнению проектной работы Паркеты, бордюры, орнаменты
Аттестационная работа. Методическая разработка по выполнению проектной работы Паркеты, бордюры, орнаменты Биологическая статистика
Биологическая статистика Вычисление скорости течения реки Березайки
Вычисление скорости течения реки Березайки Что такое функции
Что такое функции