Содержание
- 2. Системы координат на плоскости и в пространстве Что такое система координат? Рене Декарт Задание прямоугольной системы
- 3. Системы координат на плоскости и в пространстве Декартовы прямоугольные координаты О - начало координат, Ох -
- 4. Рене Декарт ДЕКАРТ (Descartes), Рене 31 марта 1596 г. – 11 февраля 1650 г. Французский философ,
- 5. Задание прямоугольной системы координат в пространстве: > Оy ┴ Оz Оz ┴ Оx Оy ┴ Оx
- 6. Вопросы: 1. Сколькими координатами может быть задана точка на прямой? Одной. 2. Сколькими координатами может быть
- 7. Выполнение задания с последующей проверкой. Начертить прямоугольную трехмерную систему координат и отметить в ней точки: А
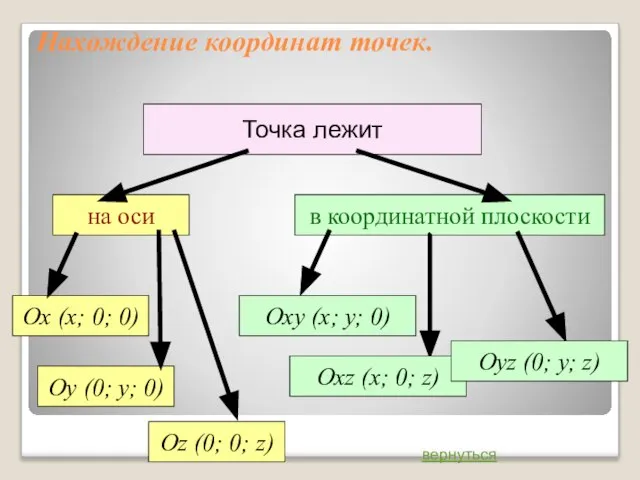
- 8. Нахождение координат точек. Точка лежит на оси Оу (0; у; 0) Ох (х; 0; 0) Оz
- 9. Повторение. Даны точки: А (2; -1; 0) В (0; 0; -7) С (2; 0; 0) D
- 10. Решение задач. Даны координаты четырех вершин куба х у z C1 - ? C - ?
- 11. Векторы Понятие вектора Коллинеарные векторы Равенство векторов Противоположные векторы Действия с векторами >>>>Вернуться на главную
- 12. Понятие вектора Пусть на тело действует сила в 8Н. Стрелка указывает направление силы, а длина отрезка
- 13. Понятие вектора Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой -
- 14. Понятие вектора На рисунках вектор изображается отрезком со стрелкой Вектор АВ, А – начало вектора, В
- 15. Понятие вектора Векторы часто обозначают и одной строчной латинской буквой со стрелкой над ней: Любая точка
- 16. Понятие вектора Длиной или модулем ненулевого вектора АВ называется длина отрезка АВ: АВ = а =
- 17. Коллинеарные векторы Ненулевые векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных
- 18. Равенство векторов Определение. Векторы называются равными, если они сонаправлены и их длины равны. а = b
- 19. Противоположные векторы Пусть а – произвольный ненулевой вектор. Определение. Вектор b называется противоположным вектору а, если
- 20. Действия с векторами Откладывание вектора от данной точки Сумма двух векторов Законы сложения Сумма нескольких векторов
- 21. Откладывание вектора от данной точки Если точка А – начало вектора а , то говорят, что
- 22. Сумма двух векторов Рассмотрим пример: Петя из дома(D) зашел к Васе(B), а потом поехал в кинотеатр(К).
- 23. Сумма двух векторов Правило треугольника Пусть а и b – два вектора. Отметим произвольную точку А
- 24. Законы сложения векторов 1) а+b=b+a (переместительный закон) Правило параллелограмма Пусть а и b – два вектора.
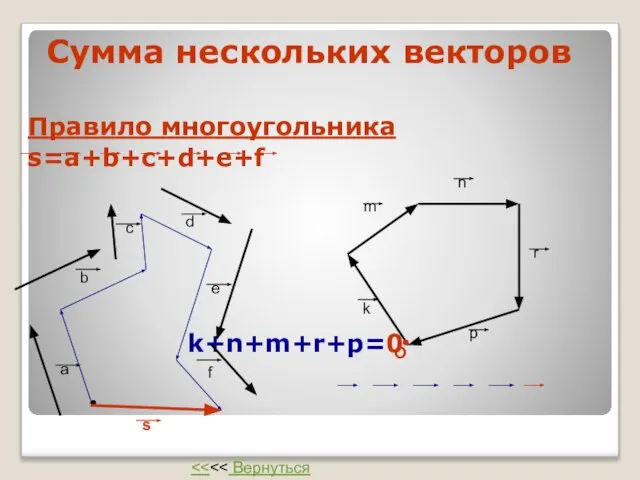
- 25. Сумма нескольких векторов Правило многоугольника s=a+b+c+d+e+f k+n+m+r+p=0 a b c d e f s k m
- 26. Вычитание векторов Определение. Разностью двух векторов а и b называется такой вектор, сумма которого с вектором
- 27. Умножение вектора на число Определение. Произведением ненулевого вектора а на число k называется такой вектор b,
- 28. Умножение вектора на число Для любых чисел k, n и любых векторов а, b справедливы равенства:
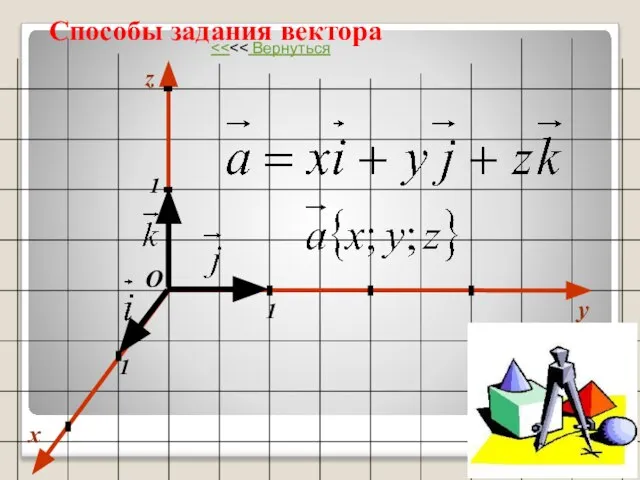
- 29. Способы задания вектора x y 1 1 1 О z
- 30. Правила действий над векторами с заданными координатами. 1. Равные векторы имеют равные координаты. Пусть , тогда
- 31. Правила действий над векторами с заданными координатами. 2. Каждая координата суммы двух (и более) векторов равна
- 32. Правила действий над векторами с заданными координатами. 3. Каждая координата произведения вектора на число равна произведению
- 33. Скалярное произведение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 34. Решение задач Задача 1 Задача 2 Задача 3 Задача 4 Повторить материал Вернуться на главную
- 35. Задача 1 Дано: ABCDA1B1C1D1 - параллелепипед. Упростите выражение: C1D-DA+CD+D1A1+AB1+CC1 К списку задач
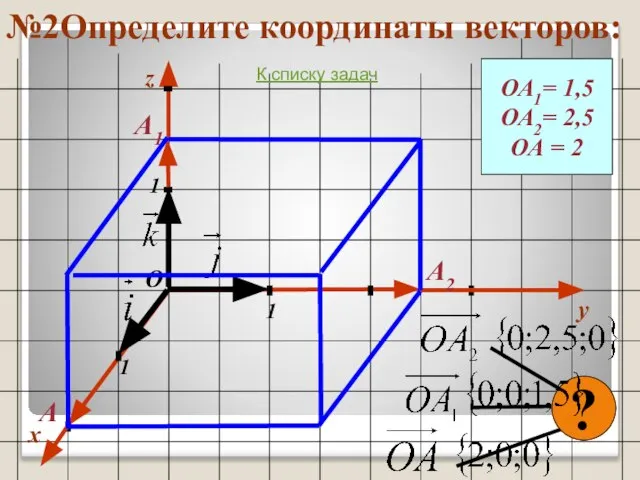
- 36. №2Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
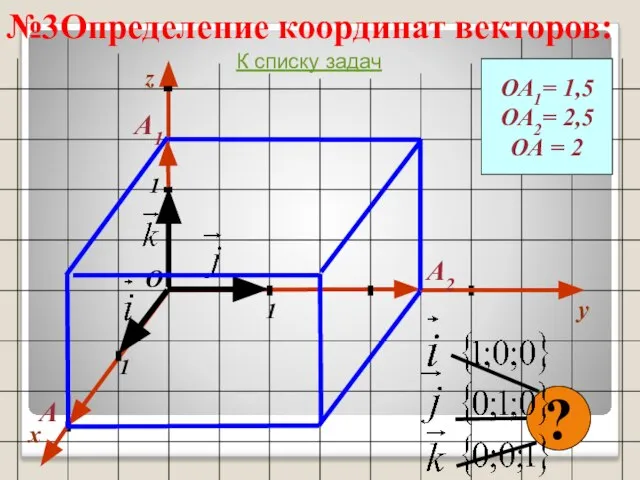
- 37. №3Определение координат векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
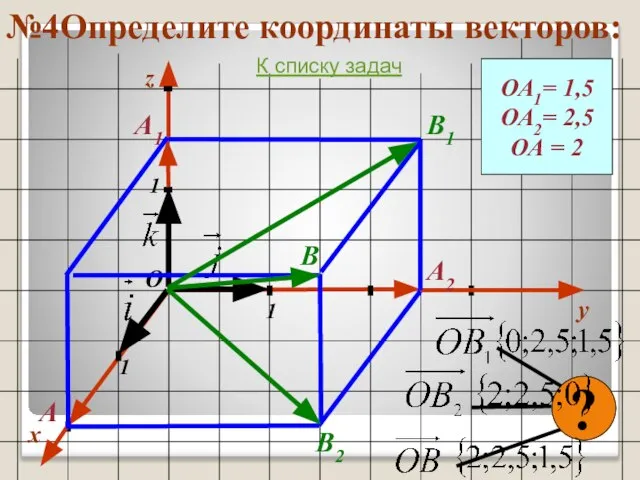
- 38. №4Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 40. Скачать презентацию































 Координатная плоскость
Координатная плоскость Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Презентация на тему Решение уравнений Математика, 5 класс
Презентация на тему Решение уравнений Математика, 5 класс Алгебра высказываний. Логика и теория алгоритмов
Алгебра высказываний. Логика и теория алгоритмов Расстояние от точки до прямой. Расстояние между параллельными прямыми
Расстояние от точки до прямой. Расстояние между параллельными прямыми Презентация на тему Второй и третий признаки подобия треугольников
Презентация на тему Второй и третий признаки подобия треугольников  формирование Икт компетентности. 5 класс
формирование Икт компетентности. 5 класс Углы треугольника
Углы треугольника Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Арифметический квадратный корень. Классная работа
Арифметический квадратный корень. Классная работа Matlab Linear Programming
Matlab Linear Programming Деление на десятичную дробь. 5 класс
Деление на десятичную дробь. 5 класс Прогнозирование. Предсказание
Прогнозирование. Предсказание Задачи по математике 5 класс
Задачи по математике 5 класс Обернена функція
Обернена функція Скалярное произведение векторов
Скалярное произведение векторов Сложение и вычитание десятичных дробей. 5 класс
Сложение и вычитание десятичных дробей. 5 класс Игры с природой
Игры с природой Презентация на тему Устные приемы вычислений в пределах 20
Презентация на тему Устные приемы вычислений в пределах 20  Тела вращения
Тела вращения Сложение натуральных чисел и его свойства. 5 класс
Сложение натуральных чисел и его свойства. 5 класс Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Преобразование графиков функций
Преобразование графиков функций Метод экспертного оценивания. Обобщение мнений экспертов
Метод экспертного оценивания. Обобщение мнений экспертов Квадратичная функция у = kх²
Квадратичная функция у = kх² Обчисліть площу плоских фігур за допомогою визначеного інтеграла. (Урок 10)
Обчисліть площу плоских фігур за допомогою визначеного інтеграла. (Урок 10) Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год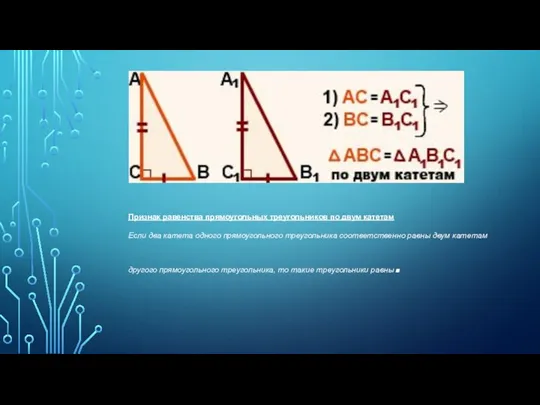 Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников