Or :
the sum of the binomial coefficients of odd rank is
Subtracting the two sum we obtain
or
The sum of the binomial coefficients of even rank is
Identities in the combination calculus( continuation)
Adding the two sums member by member we obtain:
Adding the two sums member by member we obtain:
Adding the two sums member by member we obtain:
Adding the two sums member by member we obtain:
Or :
the sum of the binomial coefficients of odd rank is
Subtracting the two sum we obtain
or
The sum of the binomial coefficients of even rank is
Adding the two sums member by member we obtain:









 Способы умножения натуральных чисел
Способы умножения натуральных чисел Решение задач
Решение задач Старинные меры длины на Руси
Старинные меры длины на Руси Показательная функция, уравнения, неравенства
Показательная функция, уравнения, неравенства «Математика – это гимнастика ума» Тем, кто учит математику, Тем,
«Математика – это гимнастика ума» Тем, кто учит математику, Тем, Вписанная и описанная окружности
Вписанная и описанная окружности Задачи на разрезание и перекраивания фигур
Задачи на разрезание и перекраивания фигур Параллельные прямые
Параллельные прямые Решение линейных уравнений с параметром и модулем
Решение линейных уравнений с параметром и модулем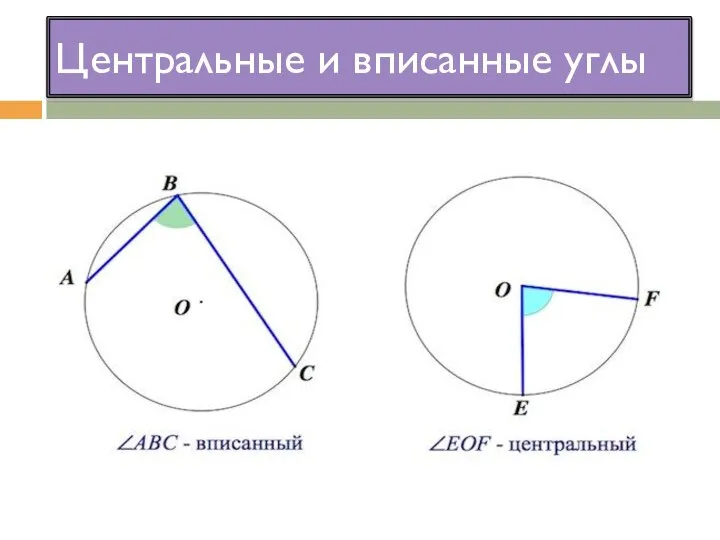 Центральные и вписанные углы
Центральные и вписанные углы Модуль числа
Модуль числа Формульная зависимость в графическом виде
Формульная зависимость в графическом виде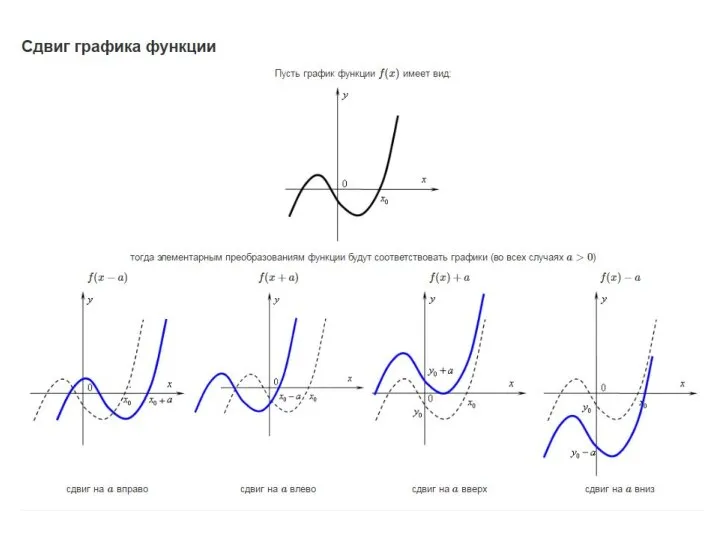 Построение эскизов кривых в декартовых координатах. (Семинар 3)
Построение эскизов кривых в декартовых координатах. (Семинар 3) Адмирал Морского Флота Федор Федорович Ушаков
Адмирал Морского Флота Федор Федорович Ушаков Вычисление площади треугольника
Вычисление площади треугольника Решение квадратных неравенств
Решение квадратных неравенств Параметры полета ракеты
Параметры полета ракеты Сравнение отрезков. Длина отрезка
Сравнение отрезков. Длина отрезка Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики
Статистические оценки параметров распределения случайных величин по выборкам. Вариационные ряды и их графики Методы параметрического спектрального анализа. Введение
Методы параметрического спектрального анализа. Введение Математика 3 класс.
Математика 3 класс.  Оболонки додатної і відʼємної Гаусової кривизни
Оболонки додатної і відʼємної Гаусової кривизни Множества и операции над ними
Множества и операции над ними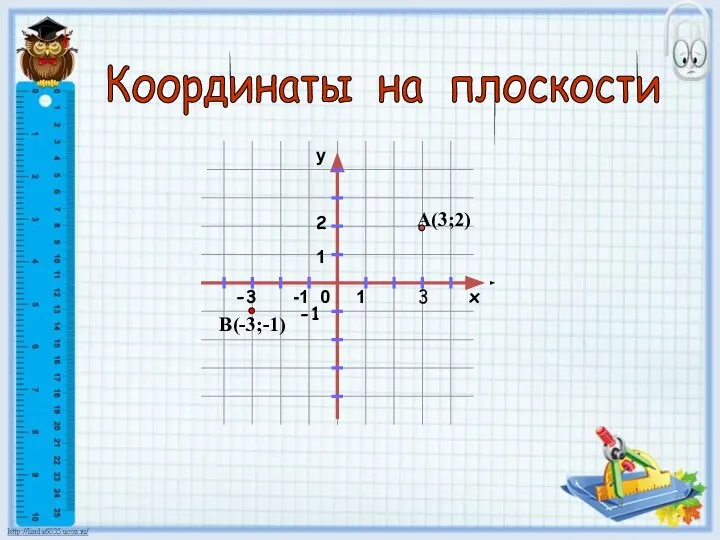 Координаты на плоскости
Координаты на плоскости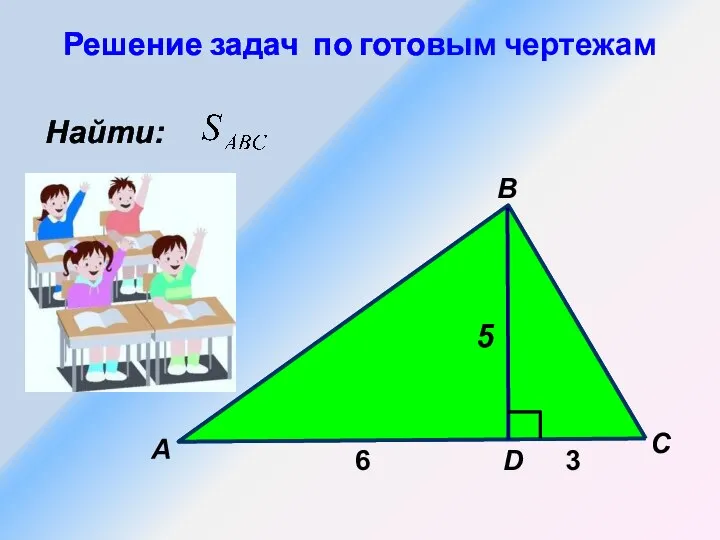 Решение задач по готовым чертежам. Теорема Пифагора
Решение задач по готовым чертежам. Теорема Пифагора Презентация по математике "Определение логарифма. Основное логарифмическое тождество" - скачать бесплатно
Презентация по математике "Определение логарифма. Основное логарифмическое тождество" - скачать бесплатно Все вокруг геометрия
Все вокруг геометрия Диаграммы. Таблицы
Диаграммы. Таблицы