Содержание
- 2. Точное оценивание погрешности однократного измерения Общая схема оценивания погрешности: 1) Путем поверки или по паспортным данным
- 3. 8) Сумма неисключенной систематической и случайной погрешности находится по формуле: Результат однократного измерения записывается в форме:
- 4. Обработка прямых измерений с многократными наблюдениями производится в слу-чаях, когда СКО погрешностей нельзя пренебречь по сравнению
- 5. Порядок выполнения операций: 1) Находят оценку измеряемой величины , за которую принимают среднее ариф-метическое значение исправленных
- 6. 8) Определяют суммарную погрешность 9) Оценивают относительную погрешность результата измерений 10) Записывают окончательный результат
- 7. Обработка результатов косвенных измерений МИ 2083-90 Государственная система обеспечения единства измерений. Измерения косвенные. Определение результатов измерений
- 8. Если интересующая нас величина Y связана с исходными величинами Хi известной функциональной зависимостью: Y =F(x1, x2,…,
- 9. Без учета знака погрешности получим максимальное значение погрешности: Если предельные значения абсолютных погрешностей Δхi неизвестны, то
- 10. При наличии случайной погрешности используются методы статистической обработ-ки. Считаем, что систематические погрешности измерений величин х1, х2,
- 11. Пример расчета погрешности косвенного измерения Вычисляемая величина Y является комбинацией физических величин x1, х2, х3 Сначала
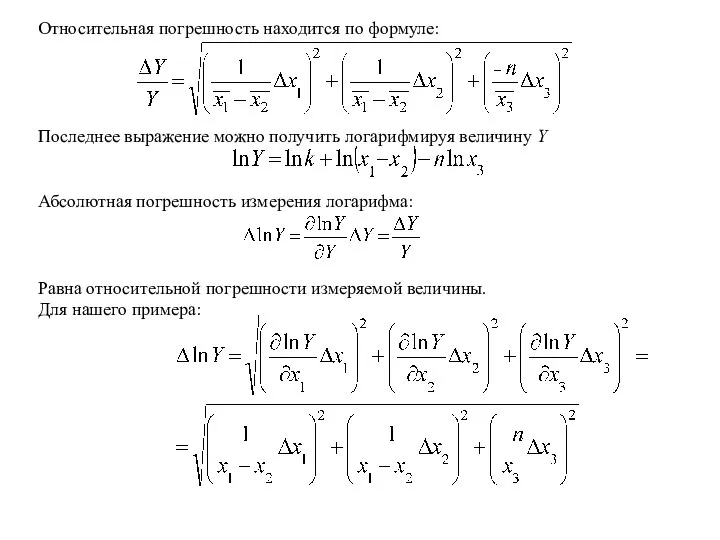
- 12. Относительная погрешность находится по формуле: Последнее выражение можно получить логарифмируя величину Y Абсолютная погрешность измерения логарифма:
- 13. Отсюда получим выражение для относительной погрешности: Примеры относительных погрешностей некоторых функций: 1)
- 14. 2)
- 15. Примеры Сопротивление Rх измерено с помощью четырехплечего моста и рассчитано по формуле Найти абсолютную ΔRх и
- 16. Относительная систематическая погрешность результата измерения сопротивления RХ находится по формуле или
- 17. Округление числа 1) Если первая из отбрасываемых цифр (считая слева направо) меньше 5, то послед-няя сохраняемая
- 18. 1. При сложении и вычитании в окончательном результате сохраняют столько деся-тичных знаков, сколько их содержится в
- 20. Скачать презентацию
















 Производная функции
Производная функции Определение угла. Развёрнутый угол
Определение угла. Развёрнутый угол Вписанная и описанная окружности
Вписанная и описанная окружности Вычисление значения функции по формуле
Вычисление значения функции по формуле Стандартный вид числа
Стандартный вид числа Сравнительный анализ
Сравнительный анализ Интерактивные тренинги по геометрии для подготовки к ОГЭ
Интерактивные тренинги по геометрии для подготовки к ОГЭ Производная функции
Производная функции Натуральные числа и дроби
Натуральные числа и дроби Презентация на тему Проценты в нашей жизни
Презентация на тему Проценты в нашей жизни Презентация по математике "Сложение и вычитание чисел" - скачать
Презентация по математике "Сложение и вычитание чисел" - скачать  Презентация по математике "Процентные вычисления и расчёты" - скачать
Презентация по математике "Процентные вычисления и расчёты" - скачать  Математика - 6. Домашнее задание
Математика - 6. Домашнее задание Преобразование графиков функций
Преобразование графиков функций Готовимся к ОГЭ по математике
Готовимся к ОГЭ по математике Координаты Подготовила и провела в 7 классе: Учитель математики и информатики Яковлева Н.С.
Координаты Подготовила и провела в 7 классе: Учитель математики и информатики Яковлева Н.С. Урок математики1 класс МОУ СОШ №128 Учитель:Лебедева Нина Ивановна Тема урока: Числа от 1 до 10. Цель урока: создать условия для закр
Урок математики1 класс МОУ СОШ №128 Учитель:Лебедева Нина Ивановна Тема урока: Числа от 1 до 10. Цель урока: создать условия для закр Уравнения, сводящиеся к квадратным
Уравнения, сводящиеся к квадратным Весёлая математика Авторы: Ульянина К., Сапожников Н., Толстова И.,Вершинин А.,Семенюта Е.
Весёлая математика Авторы: Ульянина К., Сапожников Н., Толстова И.,Вершинин А.,Семенюта Е. Презентация по математике "Решаем задачи и примеры. 2класс" - скачать
Презентация по математике "Решаем задачи и примеры. 2класс" - скачать  Куб (текше) және оның көлемі
Куб (текше) және оның көлемі Масштаб. Решение задач
Масштаб. Решение задач Сложение и вычитание обыкновенных дробей с разными знаменателями
Сложение и вычитание обыкновенных дробей с разными знаменателями Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна
Учитель математики ГБОУ СОШ№1168 г. Москвы Мишина Раиса Михайловна  Звездчатые многогранники
Звездчатые многогранники Сравнение бесконечно больших и бесконечно малых величин
Сравнение бесконечно больших и бесконечно малых величин Степень с натуральным показателем и ее свойства
Степень с натуральным показателем и ее свойства «Геометрия приближает разум к истине» Платон
«Геометрия приближает разум к истине» Платон