Определение производной

Производной функции y=f(x)
называется предел отношения
приращения функции к приращению
независимого аргумента,

Обозначения производной:

Нахождение производной функции называется
дифференцированием.

Если функция имеет конечную производную в
некоторой

Вернемся к рассматриваемым задачам.

Из задачи о касательной вытекает

Производная f / (x0)

Тогда уравнение касательной к кривой в данной точке будет иметь вид:

Из задачи о скорости движения вытекает

Производная пути по времени S /

Производная объема производимой продукции по времени u / (t0) есть производительность

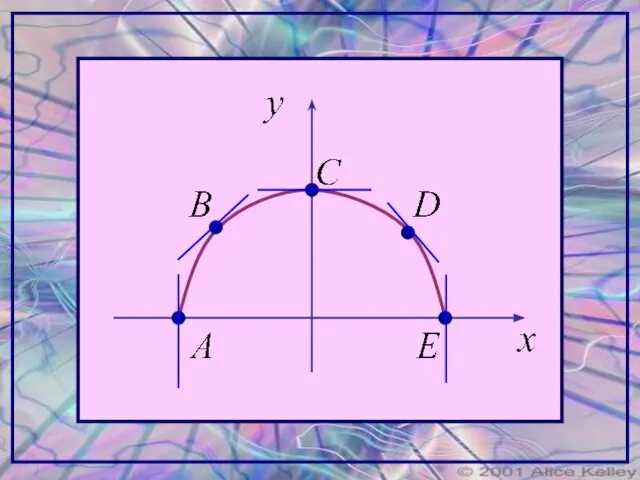
ПРИМЕР.

График функции y=f(x) есть полуокружность.
Найти f / (x) в точках A,B,C,D,E,

Из геометрического смысла производной вытекает, что производная f / (x0) есть

В точке С угол касательная параллельна оси х:

В точках А и

ТЕОРЕМА

Если функция y=f(x)
дифференцируема в точке x0,
то она непрерывна в

Доказательство:

По условию теоремы функция y=f(x) дифференцируема в точке x0 :

На основании

где α(Δx) – бесконечно малая величина при

Отсюда:

При

и

Следовательно, по

Обратная теорема, в общем случае, неверна.
Например, функция

непрерывна в точке x=0:

Проверим, будет

Т.е. общего предела не существует и функция не дифференцируема в этой