Определители. Вычисление определителей высших порядков. Свойства определителей. Алгебраические дополнения и миноры
Содержание
- 2. Понятие определителя вводится только для квадратных матриц. Пусть дана квадратная матрица A порядка n . Сопоставим
- 3. Определители третьего порядка обычно вычисляются с помощью правила Саррюса, которое символически можно определить так. Произведение элементов
- 4. Определители третьего порядка обычно вычисляются с помощью правила Саррюса, которое символически можно определить так. Произведение элементов
- 5. Пример 2. Вычислить определитель: Решение. m=n
- 6. Дадим определение определителя n-го порядка матрицы A В дальнейшем, под элементами, строками и столбцами определителя матрицы
- 7. Перед каждым произведением ставится знак "+" или "−". Определим знак перед произведением. Поскольку в каждом произведении
- 8. Инверсией называется взаимное расположение двух чисел в перестановке, когда большее предшествует меньшему. Например, в перестановке 4,1,3,6,5
- 9. §2. ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ Рассмотрим некоторые наиболее важные свойства определителей. Свойство 1. При перестановке местами двух
- 10. Свойство 5. Если в определителе вместо любой строки записать сумму этой строки и любой другой строки,
- 11. Минором любого элемента aij квадратной матрицы A порядка n называется определитель матрицы порядка n-1, которая получается
- 12. Свойство 9. Определитель квадратной матрицы равен сумме произведений элементов некоторой строки или столбца на их алгебраические
- 13. Пример 3. Вычислить определитель матрицы Решение. Для вычисления определителя выберем первый столбец, поскольку в нём есть
- 15. Скачать презентацию












 Вероятность и статистика на ЕГЭ
Вероятность и статистика на ЕГЭ Определение квадратного уравнения. Неполные квадратные уравнения
Определение квадратного уравнения. Неполные квадратные уравнения Скачать презентацию Острова Атлантического океана БЕРМУДЫ
Скачать презентацию Острова Атлантического океана БЕРМУДЫ  Списки
Списки Презентация по математике "Функция. Область определения и множество значений." - скачать
Презентация по математике "Функция. Область определения и множество значений." - скачать  Решение задач с помощью уравнений. 7 класс
Решение задач с помощью уравнений. 7 класс Дифференциал функции
Дифференциал функции Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа
Решение нестандартных задач в рамках итогового повторения курса алгебры и начала анализа Приложения производной
Приложения производной Использование нетрадиционных методов при подготовке к ЕГЭ по математике
Использование нетрадиционных методов при подготовке к ЕГЭ по математике Математика 3 класс, II четверть Тема урока Решение задач.
Математика 3 класс, II четверть Тема урока Решение задач.  Построение точек, линий и направлений
Построение точек, линий и направлений Градусник. Приложение 2
Градусник. Приложение 2 Обзор численных методов
Обзор численных методов Распредели предметы поровну. 2 класс
Распредели предметы поровну. 2 класс ОГЭ. Открытый банк заданий по математике. Задачи
ОГЭ. Открытый банк заданий по математике. Задачи Математика и искусство
Математика и искусство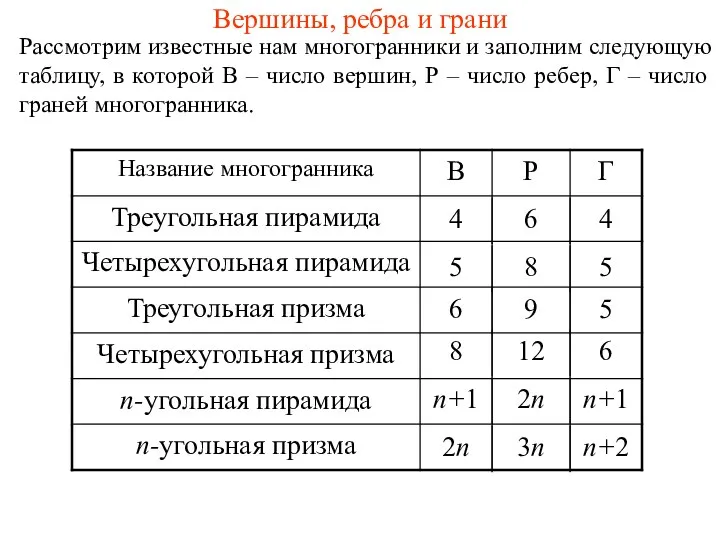 Вершины, ребра и грани
Вершины, ребра и грани Методические рекомендации по изложению темы «Площади плоских фигур» по геометрии в 7 - 9 классах
Методические рекомендации по изложению темы «Площади плоских фигур» по геометрии в 7 - 9 классах Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Урок 32
Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Урок 32 Брейн-ринг. Математическая игра
Брейн-ринг. Математическая игра Корень n-й степени из действительного числа (11 класс)
Корень n-й степени из действительного числа (11 класс) Мир координат
Мир координат Cложение и вычитание алгебраических дробей с разными знаменателями. 8 класс
Cложение и вычитание алгебраических дробей с разными знаменателями. 8 класс Discrete Probability Distributions: Binomial and Poisson Distribution. Week 7 (2)
Discrete Probability Distributions: Binomial and Poisson Distribution. Week 7 (2) Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов
Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов Сложение чисел с разными знаками. 6 класс
Сложение чисел с разными знаками. 6 класс Применение подобия для решения задач
Применение подобия для решения задач