Содержание
- 2. Предмет вычислительной математики Математическая модель –приближенное математическое описание объекта (технологического процесса, реакции, явления и т.д.). Математическое
- 3. Основные понятия: метрические пространства Главная задача численных методов – фактическое нахождение решения с требуемой или, по
- 4. Линейные пространства Линейное пространство- частный случай метрического. В нем определены операции сложения элементов и умножения их
- 5. Линейные нормированные пространства. Линейное пространство L называется нормированным, если введена норма : 1) - вещественное число
- 6. Сходящиеся и фундаментальные последовательности, открытые и замкнутые шары. Полные метрические пространства. Последовательность элементов метрического пространства xn
- 7. Примеры полных метрических пространств 1. R – множество вещественных чисел. и 2. Rn - пространство векторов
- 8. Примеры метрических пространств 4. L2 [a, b ] – множество функций интегрируемых с квадратом на [a,
- 9. Элементы общей теории погрешностей и компьютерной арифметики. Основные определения, утверждения, примеры Точность решения задачи оценивается абсолютной
- 10. Элементы общей теории погрешностей и компьютерной арифметики. Основные определения, утверждения, примеры Неустранимая погрешность обусловлена неточностью исходных
- 11. Элементы общей теории погрешностей и компьютерной арифметики. Основные определения, утверждения, примеры Пусть решение y, соответствует входным
- 12. Элементы общей теории погрешностей и компьютерной арифметики. Основные определения, утверждения, примеры Рассмотрим подробнее погрешность округления чисел,
- 13. Элементы общей теории погрешностей и компьютерной арифметики. Основные определения, утверждения, примеры В ЭВМ чаще всего используется
- 14. Примеры Пример 1. Необходимо отыскать минимальный корень уравнения. Вычисления производим в десятичной системе счисления, причем в
- 15. Примеры Как видно из сравнения полученных результатов, применение "неудачного" алгоритма завышает результат на 30 %. Это
- 16. Примеры Пример 2 Требуется вычислить: Сложим эти числа столбиком и, округлив результат до 3-х значащих цифр,
- 17. Примеры Пусть теперь выражение записано в обратном порядке: Выполним суммирование как ЭВМ: + 83 + 109
- 18. Погрешности арифметических операций Погрешность вычисления функций:
- 19. Рекомендации для снижения ошибок округления: В машинной арифметике законы коммутативности (переместительный) и дистрибутивности (распределительный) не всегда
- 20. При выборе численного метода решения задачи необходимо учитывать следующее Погрешность метода должна быть на порядок меньше
- 21. Для оценки погрешности решения на практике можно использовать следующие приемы: Решить задачу различными численными методами и
- 22. Прямые и итерационные методы и алгоритмы решения математических задач Прямые и итерационные методы решения математических задач.
- 23. Прямые (точные) численные методы и алгоритмы Решение будет получено за конечное число шагов; Количество шагов и
- 24. Итерационные численные методы и алгоритмы Решение определяется как предел бесконечной итерационной последовательности; Определены правила получения итерационной
- 25. Преимущества, недостатки и особенности реализации алгоритмов для прямых методов Преимущество: В отсутствие вычислительной погрешности дают точный
- 26. Преимущества, недостатки и особенности реализации алгоритмов для прямых методов Особенности реализации: Требуют исследования влияния ошибок округления
- 27. Преимущества, недостатки и особенности реализации алгоритмов для итерационных методов Преимущество: Вычислительная погрешность не накапливается и даже
- 29. Скачать презентацию






![Примеры метрических пространств 4. L2 [a, b ] – множество функций](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1468342/slide-7.jpg)



















 Графики функций y = a (x-m)^2
Графики функций y = a (x-m)^2 Угловой коэффициент в уравнении прямой (8 класс) - Презентация_
Угловой коэффициент в уравнении прямой (8 класс) - Презентация_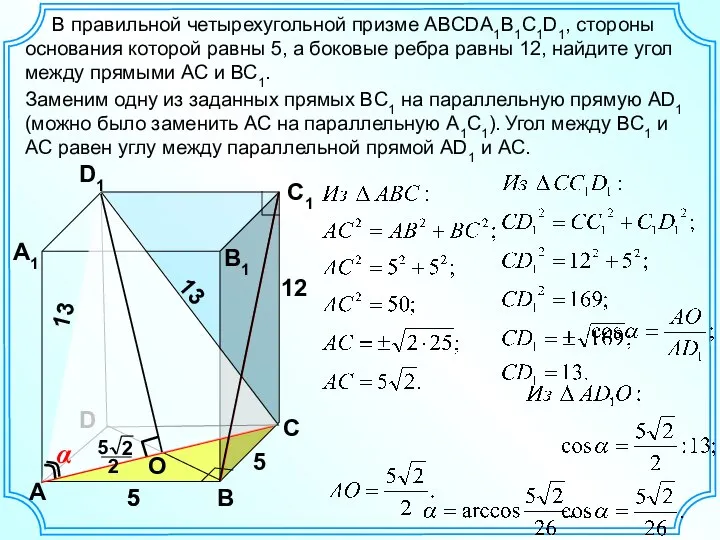 Задача 38
Задача 38 Аттестационная работа. Решение задач повышенной сложности
Аттестационная работа. Решение задач повышенной сложности Квадратные уравнения и способы их решения
Квадратные уравнения и способы их решения Презентация по математике "Числа в нашей жизни" - скачать
Презентация по математике "Числа в нашей жизни" - скачать  Деление взаимно обратных чисел
Деление взаимно обратных чисел Замечательные кривые в математике Рудницкая Мария Соболь Анастасия Ученицы 11 « А» класс ГОУ ЦО № 1453 г. Москвы Руководитель: Ива
Замечательные кривые в математике Рудницкая Мария Соболь Анастасия Ученицы 11 « А» класс ГОУ ЦО № 1453 г. Москвы Руководитель: Ива Логарифмическая функция, ее график и свойства
Логарифмическая функция, ее график и свойства 24.02.2010г. Дифференцирование частного и степени. Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ»
24.02.2010г. Дифференцирование частного и степени. Дернова А.М. учитель математики Iкв.к. МБОУ «Новотроицкая СОШ» Линейность изображений
Линейность изображений Презентация по математике "Угол, вписанный в окружность " - скачать
Презентация по математике "Угол, вписанный в окружность " - скачать  Презентация по математике "Умножение положительных и отрицательных чисел" - скачать бесплатно
Презентация по математике "Умножение положительных и отрицательных чисел" - скачать бесплатно Операції над множинами
Операції над множинами Построение графиков функций с помощью производных
Построение графиков функций с помощью производных Деление круглого двузначного числа на круглое двузначное число
Деление круглого двузначного числа на круглое двузначное число Основные тригонометрические формулы
Основные тригонометрические формулы Заморочки из бочки. Урок-игра «Счастливый случай»
Заморочки из бочки. Урок-игра «Счастливый случай» Единицы длины. (2 класс)
Единицы длины. (2 класс) Проценты. Решение задач
Проценты. Решение задач Правильные многогранники
Правильные многогранники Скалярное произведение векторов
Скалярное произведение векторов Упрощение выражений
Упрощение выражений Логарифмы и их свойства. Готовимся к ЕГЭ
Логарифмы и их свойства. Готовимся к ЕГЭ Игра «Математик-бизнесмен»
Игра «Математик-бизнесмен» Прикладна математика
Прикладна математика Теория вероятностей, математическая статистика и случанйные процессы
Теория вероятностей, математическая статистика и случанйные процессы Множественная регрессия и корреляция
Множественная регрессия и корреляция