Содержание
- 2. Приближенные и точные числа Точные числа выражают безошибочное значение каких-либо величин и обычно имеют математическое происхождение
- 3. Приближенные и точные числа После того, как погрешность записана, значение результата должно быть округлено таким образом,
- 4. Умножение приближенных чисел Сложение приближенных чисел: Предельная относительная ошибка произведения: y±Δy=(a ± Δa)(b ± Δb) равна
- 5. Возведение приближенного числа в степень При возведении приближенного числа a в степень n an = a
- 6. Общая формула для предельной относительной ошибки функции Предельная относительная ошибка функции одного аргумента f(a) равна произведению
- 7. Общая формула для предельной относительной ошибки функции Алгоритм нахождения предельной относительной ошибки функции произвольного вида: Логарифмировать
- 8. Формулы для предельной относительной ошибки функций
- 9. Средняя квадратичная ошибка функции Для функции f(a,b,c,…) составленной из приближенных чисел можно записать среднюю квадратичную ошибку
- 10. Обработка результатов измерений Если одна физическая величина зависит от другой величины то эту зависимость можно исследовать
- 11. Регрессионный анализ Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких
- 12. Регрессионный анализ Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких
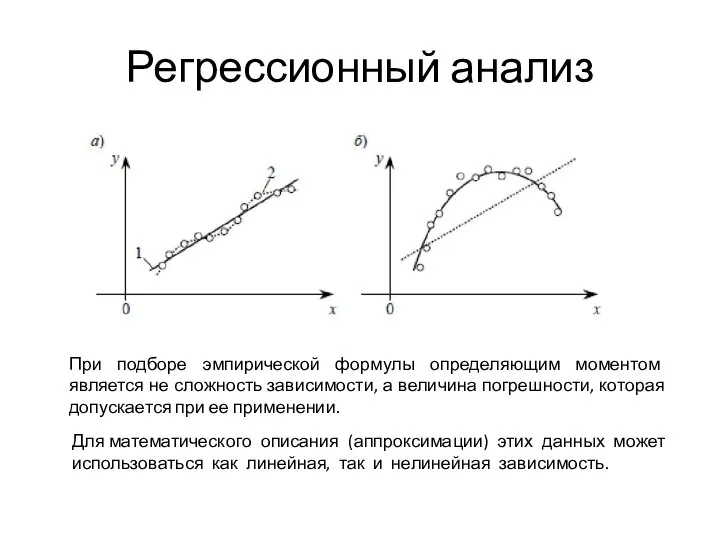
- 13. Регрессионный анализ При подборе эмпирической формулы определяющим моментом является не сложность зависимости, а величина погрешности, которая
- 14. Регрессионный анализ Выбор вида эмпирической зависимости целесообразно осуществлять с учетом физических закономерностей исследуемого процесса. Например падение
- 15. Регрессионный анализ Выбор коэффициентов эмпирической зависимости Аппроксимационная зависимость описывается в виде некоторой функции: Которая имеет m
- 16. Регрессионный анализ Два подхода к проблеме выбора коэффициентов эмпирической зависимости Интерполирование – обеспечение условия совладения вычислений
- 17. Регрессионный анализ Непрерывная аппроксимация f(x) – исходная функция. φ(x) – аппроксимирующая функция. При условии минимального отклонения
- 19. Скачать презентацию















 Бинарные (фиктивные) переменные
Бинарные (фиктивные) переменные Графический метод решения ЗЛП Лекция 5
Графический метод решения ЗЛП Лекция 5  Наибольший общий делитель. 5 класс
Наибольший общий делитель. 5 класс Терминологический словарь Прямоугольник Квадрат Параллелепипед Куб Периметр Площадь Площадь поверхности Объём
Терминологический словарь Прямоугольник Квадрат Параллелепипед Куб Периметр Площадь Площадь поверхности Объём  Инструменты для проверки качества грида. Обзор
Инструменты для проверки качества грида. Обзор Двугранный угол. Угол между плоскостями
Двугранный угол. Угол между плоскостями Что такое «геометрия»?
Что такое «геометрия»? История чисел Работа ученицы 8 а класса МОУ СОШ №7 г. Соль – Илецка Оренбургской области Музапаровой Асемгуль
История чисел Работа ученицы 8 а класса МОУ СОШ №7 г. Соль – Илецка Оренбургской области Музапаровой Асемгуль Тригонометрические уравнения
Тригонометрические уравнения Числовые множества
Числовые множества Контрольная работа № 1. Вариант 0
Контрольная работа № 1. Вариант 0 Фундаментальные циклы
Фундаментальные циклы О графиках
О графиках Готовимся к ЕГЭ. Задача 16
Готовимся к ЕГЭ. Задача 16 Возможные варианты внутренней структуры треугольника
Возможные варианты внутренней структуры треугольника Вероятность события 9 класс
Вероятность события 9 класс  Формула Пика. Ее применение при решении задач. (9 класс)
Формула Пика. Ее применение при решении задач. (9 класс) Конкурс интерактивных презентаций «Интерактивная мозаика» www.Pedsovet.su автор: Кондратьева Тамара Станиславовна ГОУ СОШ № 534, гор
Конкурс интерактивных презентаций «Интерактивная мозаика» www.Pedsovet.su автор: Кондратьева Тамара Станиславовна ГОУ СОШ № 534, гор Особенности построения фазовых портретов
Особенности построения фазовых портретов Методики выполнения измерений, как основа метрологического обеспечения
Методики выполнения измерений, как основа метрологического обеспечения Десятичная система счисления
Десятичная система счисления Статистические критерии в спортивной метрологии
Статистические критерии в спортивной метрологии Скалярное произведение векторов. Угол между векторами
Скалярное произведение векторов. Угол между векторами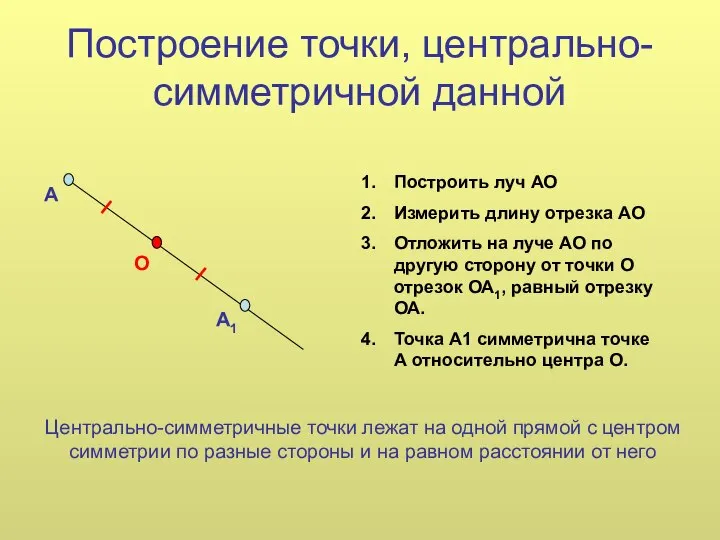 Построение точки, центрально-симметричной данной
Построение точки, центрально-симметричной данной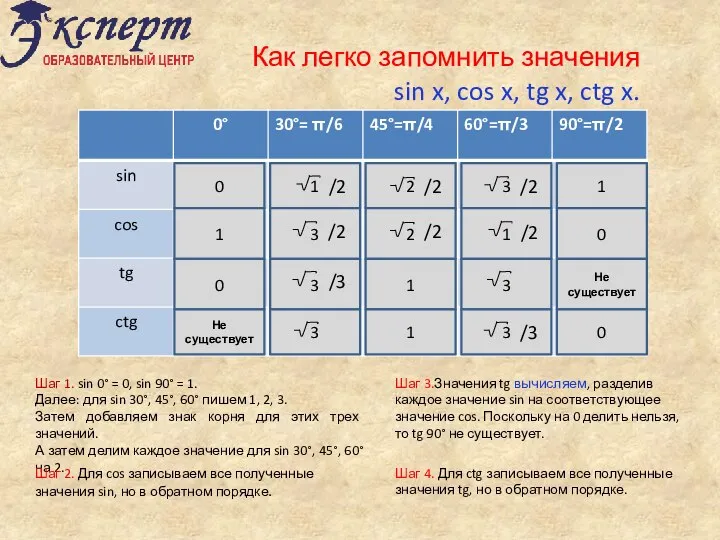 Как легко запомнить значения sin x, cos x, tg x, ctg x
Как легко запомнить значения sin x, cos x, tg x, ctg x Противоположные числа
Противоположные числа Золотое сечение - божественная мера красоты
Золотое сечение - божественная мера красоты Тригонометрия. Формулы приведения
Тригонометрия. Формулы приведения