Основы практической био-медицинской статистики. Методы непараметрической статистики. Хи-квадрат. Точный тест Фишера
Содержание
- 2. Непараметрическая статистика (классически): Если зависимая (измеряемая) переменная не численная (порядковая или качественная); Если численная зависимая переменная
- 3. Предположения (ограничения) для точного критерия Фишера и критерия хи-квадрат: Случайная выборка (данные должны быть отобраны из
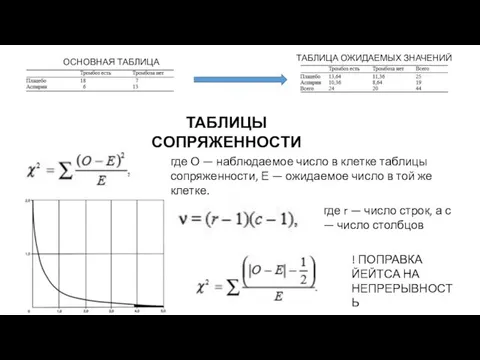
- 4. ОСНОВНАЯ ТАБЛИЦА ТАБЛИЦА ОЖИДАЕМЫХ ЗНАЧЕНИЙ ТАБЛИЦЫ СОПРЯЖЕННОСТИ где О — наблюдаемое число в клетке таблицы сопряженности,
- 5. ЕСЛИ ОЖИДАЕМЫЕ ЗНАЧЕНИЯ ВО ВСЕХ КЛЕТКАХ БОЛЕЕ 5! ИНАЧЕ – ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА! Построив все остальные
- 6. Если таблица больше чем 2х2 – тяжело оценить за счет чего таблица несимметрична! Что делать: Попарные
- 7. Непараметрический аналог непарного t-теста: тест суммы рангов Уилкоксона-Манн-Уитни t-тест основывается на предположении, что выборка сделана из
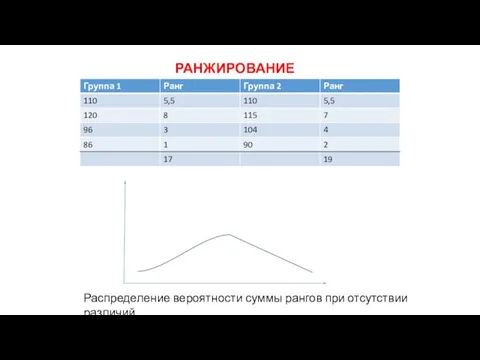
- 8. РАНЖИРОВАНИЕ Распределение вероятности суммы рангов при отсутствии различий
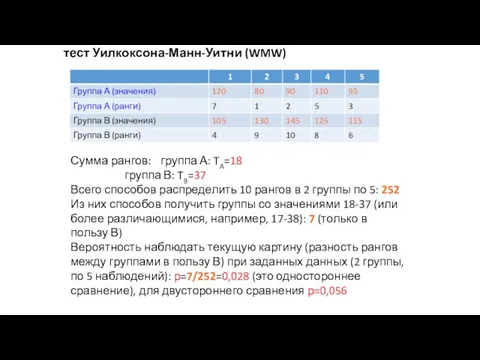
- 9. тест Уилкоксона-Манн-Уитни (WMW) Сумма рангов: группа А: TA=18 группа В: TB=37 Всего способов распределить 10 рангов
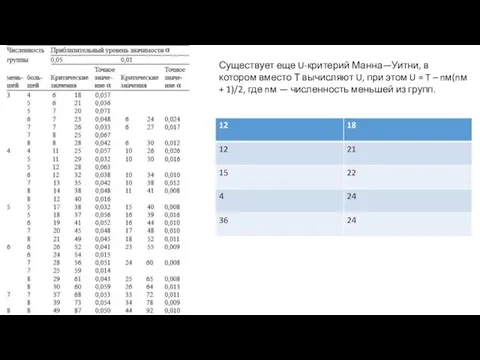
- 10. Существует еще U-критерий Манна—Уитни, в котором вместо Т вычисляют U, при этом U = T –
- 11. тест Уилкоксона-Манн-Уитни (WMW) Ответ на вопрос: Если бы распределение рангов между группами А и В было
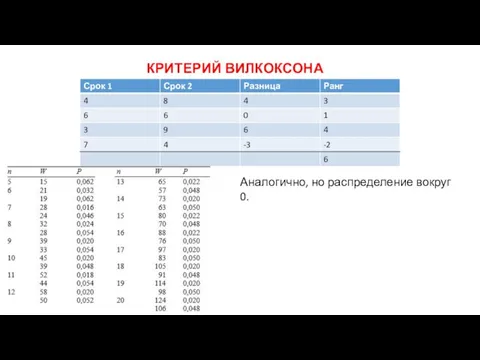
- 12. КРИТЕРИЙ ВИЛКОКСОНА Аналогично, но распределение вокруг 0.
- 13. КРИТЕРИЙ КРАСКЕЛА-УОЛЛИСА • Объединив все наблюдения, упорядочить их по возрастанию, ранжировать. • Вычислить критерий Краскела—Уоллиса Н.
- 15. Скачать презентацию







 Средняя линия треугольника
Средняя линия треугольника Математика. Задания повышенного и высокого уровней сложности
Математика. Задания повышенного и высокого уровней сложности Математические гонки. Интерактивный тренажёр. Счёт в пределах 10
Математические гонки. Интерактивный тренажёр. Счёт в пределах 10 Смежные и вертикальные углы
Смежные и вертикальные углы Что такое математика?
Что такое математика? Действия с натуральными числами
Действия с натуральными числами Parallogramm
Parallogramm Зорина Светлана Юрьевна учитель начальных классов МОУ «Гимназия № 83», г. Ижевск
Зорина Светлана Юрьевна учитель начальных классов МОУ «Гимназия № 83», г. Ижевск График равномерного движения
График равномерного движения Обратная пропорциональность
Обратная пропорциональность Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Математик на фабрике обоев или алгоритмическое рисование узоров
Математик на фабрике обоев или алгоритмическое рисование узоров Признаки делимости на 3 и 9
Признаки делимости на 3 и 9 Понятие вектора
Понятие вектора Решение иррациональных уравнений и неравенств. 10 класс
Решение иррациональных уравнений и неравенств. 10 класс Методы решения уравнений третьей степени. Простейший. Графический. Способ группировки (А, В, С) Метод подбора. Искусственный мет
Методы решения уравнений третьей степени. Простейший. Графический. Способ группировки (А, В, С) Метод подбора. Искусственный мет Від’ємні числа, дії над ними
Від’ємні числа, дії над ними Презентация Оценка разности
Презентация Оценка разности  Координатный луч Урок математики в 5 классе Презентацию подготовил учитель математики МОУ»Шулкинская средняя школа» Романо
Координатный луч Урок математики в 5 классе Презентацию подготовил учитель математики МОУ»Шулкинская средняя школа» Романо Начальные сведения из теории вероятностей. 9 класс
Начальные сведения из теории вероятностей. 9 класс Прямая задача теории погрешности. Лекция 3
Прямая задача теории погрешности. Лекция 3 Признаки параллельности прямых. Задачи
Признаки параллельности прямых. Задачи Сравнение бесконечно больших и бесконечно малых величин
Сравнение бесконечно больших и бесконечно малых величин Решение неравенств с одной переменной
Решение неравенств с одной переменной Первообразная и интеграл
Первообразная и интеграл Основы метрологического обеспечения
Основы метрологического обеспечения Линия уравнений и неравенств в курсе алгебры основной школы
Линия уравнений и неравенств в курсе алгебры основной школы Презентация по математике "Введение вероятностно-статистической линии в школьный курс математики 5-6 классов" - скачать
Презентация по математике "Введение вероятностно-статистической линии в школьный курс математики 5-6 классов" - скачать