Содержание
- 2. Тема 7. Дискретные случайные процессы 7. Дискретные случайные процессы 7.1. О характеристиках случайных величин 7.2. О
- 3. 7.3. Преобразование случайного стационарного процесса линейной непрерывной системой Постановка задачи. Пусть имеется устойчивая линейная непрерывная система,
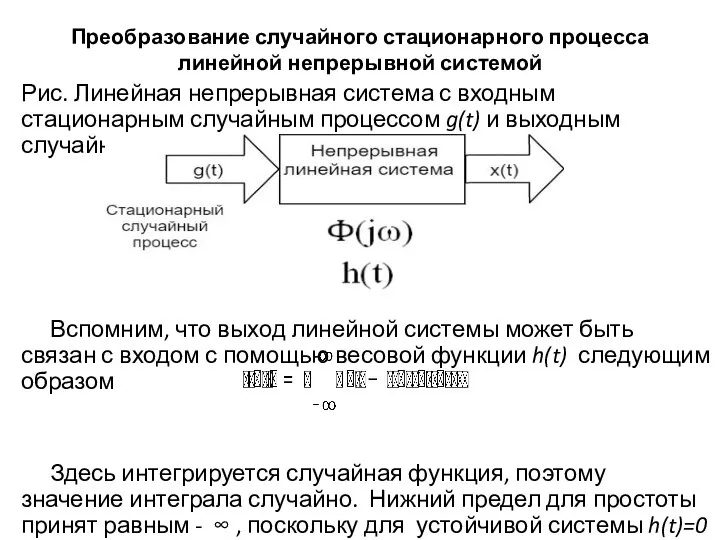
- 4. Преобразование случайного стационарного процесса линейной непрерывной системой Рис. Линейная непрерывная система с входным стационарным случайным процессом
- 5. Преобразование случайного стационарного процесса линейной непрерывной системой Усредняя случайные функции в обеих частях приведенного выше выражения,
- 6. Преобразование случайного стационарного процесса линейной непрерывной системой
- 7. Преобразование случайного стационарного процесса линейной непрерывной системой Однако до окончания переходного процесса матожидание выхода может меняться
- 8. Преобразование случайного стационарного процесса линейной непрерывной системой Поскольку спектры G(jω) и X(jω) – это случайные функции,
- 9. Преобразование случайного стационарного процесса линейной непрерывной системой Поскольку вывод выражения для корреляционной функции выхода более громоздкий,
- 10. Преобразование случайного стационарного процесса линейной непрерывной системой Замечание (о спектральной факторизации) Выражение Sx(ω) = | Ф(
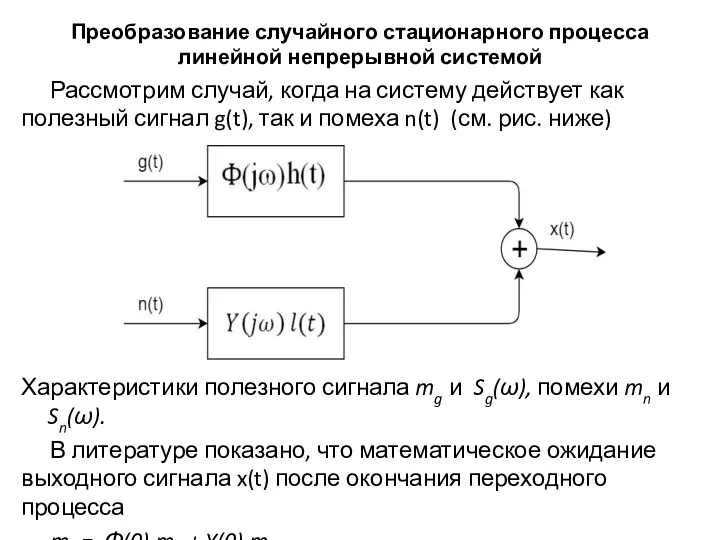
- 11. Преобразование случайного стационарного процесса линейной непрерывной системой Рассмотрим случай, когда на систему действует как полезный сигнал
- 12. Преобразование случайного стационарного процесса линейной непрерывной системой Получим выражение для спектральной плотности Sx(ω) выхода. Для этого
- 13. Преобразование случайного стационарного процесса линейной непрерывной системой Усредняем: Sgn(ω) и Sng(ω) – взаимные спектральные плотности Если
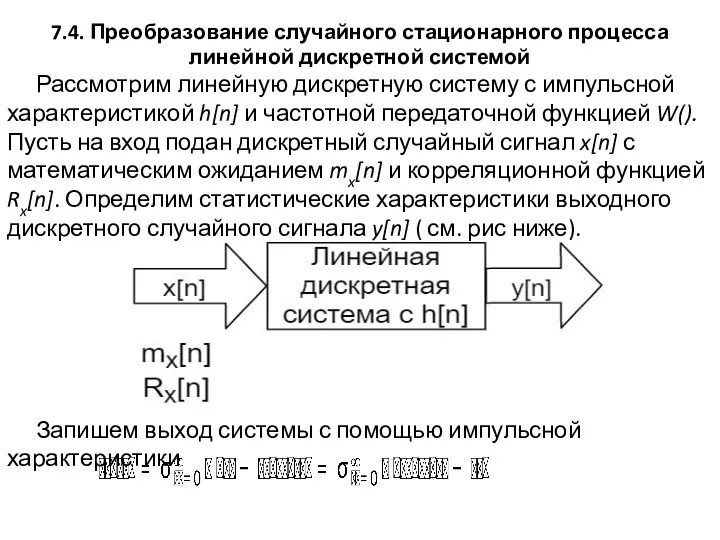
- 14. 7.4. Преобразование случайного стационарного процесса линейной дискретной системой Рассмотрим линейную дискретную систему с импульсной характеристикой h[n]
- 15. Преобразование случайного стационарного процесса линейной дискретной системой Возьмем матожидание от всех реализаций случайных процессов Таким образом,
- 16. Преобразование случайного стационарного процесса линейной дискретной системой Cреднеквадратичное значение выхода y[n] Поскольку выражение в фигурных скобках
- 17. Преобразование случайного стационарного процесса линейной дискретной системой Учитывая множитель , получим соотношение между средними мощностями входа
- 18. Преобразование случайного стационарного процесса линейной дискретной системой Корреляционная функция выхода
- 19. Преобразование случайного стационарного процесса линейной дискретной системой Спектральная плотность выхода как преобразование Фурье от корреляционной функции
- 20. Преобразование случайного стационарного процесса линейной дискретной системой Полученный результат можно трактовать так. Спектральная плотность выхода равна
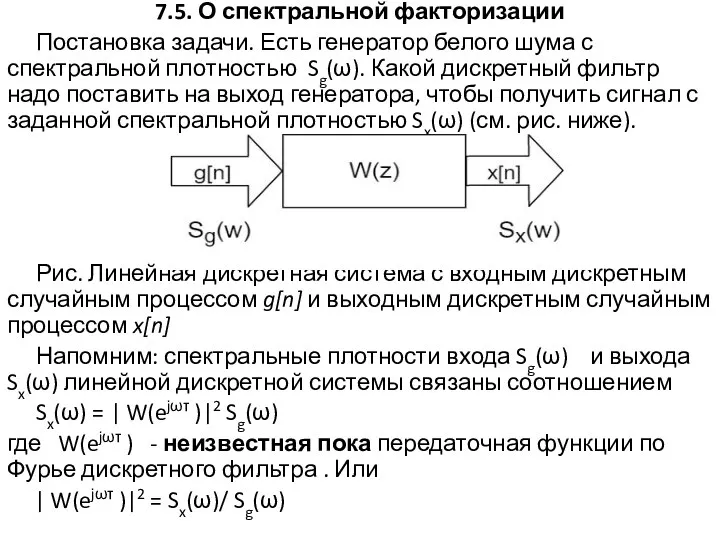
- 21. 7.5. О спектральной факторизации Постановка задачи. Есть генератор белого шума с спектральной плотностью Sg(ω). Какой дискретный
- 22. О спектральной факторизации Вспомним соотношение, связывающее передаточную функцию по Фурье W(ejωτ) дискретного фильтра с его импульсной
- 23. О спектральной факторизации 5. Нули и полюса, расположенные внутри круга единичного радиуса, образуют импульсную передаточную функцию
- 24. О спектральной факторизации Или 2. Сделать замену ejωτ =z 3. Найти коэффициенты числителя b=[b0,b1, ] и
- 25. О спектральной факторизации 4. Воспользуемся функцией пакета MATLAB, которая найдет нули и полюса полученных в предыдущем
- 26. О спектральной факторизации 5. Нули и полюса, расположенные внутри круга единичного радиуса, образуют импульсную передаточную функцию
- 28. Скачать презентацию











![Преобразование случайного стационарного процесса линейной дискретной системой Cреднеквадратичное значение выхода y[n]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/714009/slide-15.jpg)









 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости Полиномы над полями конечной характеристики
Полиномы над полями конечной характеристики Матрицы. Определения
Матрицы. Определения Булева алгебра
Булева алгебра Математика в изобразительном искусстве
Математика в изобразительном искусстве Презентация на тему Обозначение натуральных чисел. 5 класс.
Презентация на тему Обозначение натуральных чисел. 5 класс.  Преобразование Фурье
Преобразование Фурье Статистическое наблюдение. Тема 2
Статистическое наблюдение. Тема 2 Круговые диаграммы
Круговые диаграммы Умножение десятичных дробей
Умножение десятичных дробей Декартово произведение
Декартово произведение Признаки равенства треугольников
Признаки равенства треугольников Решение заданий С2
Решение заданий С2 Квадратичная функция и её график
Квадратичная функция и её график Числа Фибоначчи
Числа Фибоначчи Линейная функция. Построение графика функции у= 2х-1
Линейная функция. Построение графика функции у= 2х-1 Типы задач на дроби
Типы задач на дроби Исследование качества школьного математического и естественнонаучного образования TIMSS
Исследование качества школьного математического и естественнонаучного образования TIMSS Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000
Кластеризация значений пикселей изображений с учетом метрики цветового различия CIEDE-2000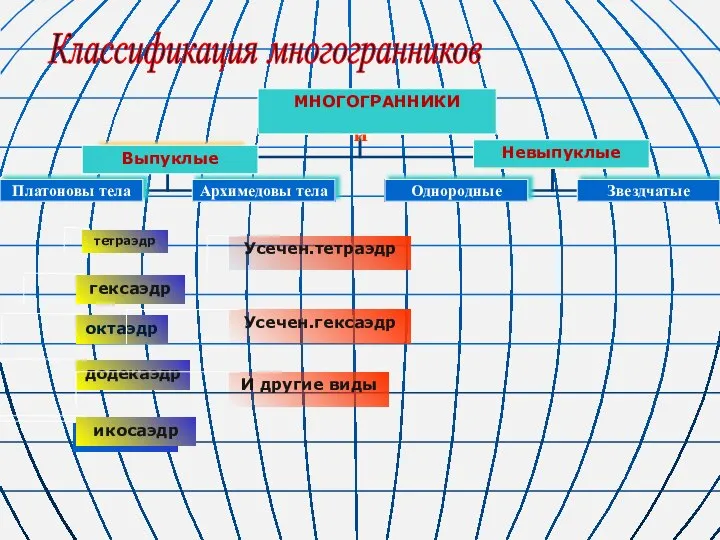 Классификация многогранников
Классификация многогранников Способ подстановки
Способ подстановки 20180306_prezentatsiya
20180306_prezentatsiya Что такое алгебра?
Что такое алгебра? Уравнения прямой и окружности
Уравнения прямой и окружности Длина окружности. Площадь круга
Длина окружности. Площадь круга Правильные многогранники
Правильные многогранники Решение уравнений tgx=a. Понятие арктангенса числа
Решение уравнений tgx=a. Понятие арктангенса числа