Содержание
- 2. Цели лекции Раскрыть понятие регрессии. Познакомиться с методом наименьших квадратов – методом построения линейного уравнения регрессии.
- 3. Виды зависимостей между переменными 1. Функциональные: Y = f(X). Имеют место при исследовании связей между неслучайными
- 4. Виды статистических зависимостей а) Корреляционные: при изменении одной из величин изменяется среднее значение другой (связь между
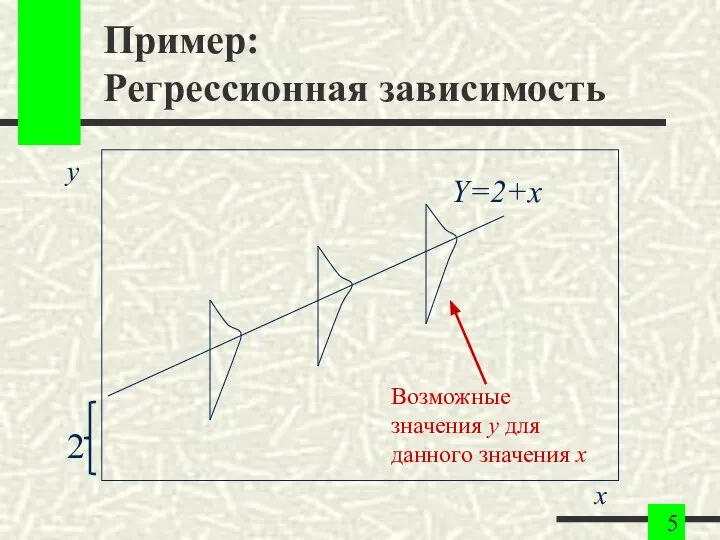
- 5. Пример: Регрессионная зависимость y 2 Y=2+x Возможные значения y для данного значения x x
- 6. Что такое регрессионный анализ? Регрессионный анализ – наиболее часто используемый инструмент в эконометрике. Регрессионный анализ представляет
- 7. Определение регрессии Регрессия – функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой
- 8. Регрессионные модели Mx[Y] = ϕ(X) − парная регрессия, Mx[Y] = ϕ(X1,…,Xm) − множественная регрессия, где ϕ(X)
- 9. Пример: Парная регрессия Мы хотим определить зависимость между продажами и затратами на рекламу. y – продажи.
- 10. Пример: Множественная регрессия Мы хотим определить связь между потреблением, доходом семьи, финансовыми активами семьи и размером
- 11. Регрессионные уравнения Y = M[Y/x] + ε = ϕ(x) + ε − уравнение парной регрессии, Y
- 12. Причины обязательного присутствия случайного фактора Невключение в модель всех объясняющих переменных. Неправильный выбор функциональной формы модели.
- 13. Этапы построения качественного уравнения регрессии 1. Определение конечных целей эконометрического моделирования, набора участвующих в модели факторов
- 14. Этапы построения качественного уравнения регрессии 4. Выбор формулы уравнения регрессии (спецификация уравнения регрессии). 5. Определение параметров
- 15. Выбор формы парной регрессии В случае парной регрессии выбор формулы обычно осуществляется по графическому изображению реальных
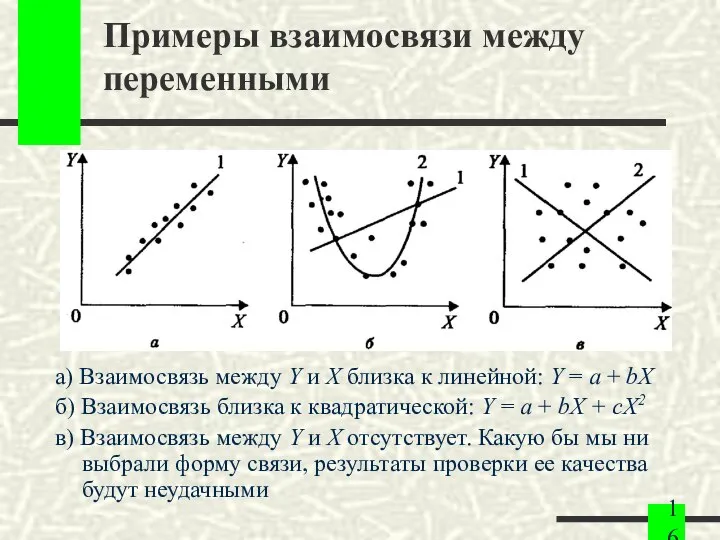
- 16. Примеры взаимосвязи между переменными а) Взаимосвязь между Y и X близка к линейной: Y = a
- 17. Парная линейная регрессия Модель линейной регрессии является наиболее распространенной (и простой) зависимостью между переменными, а также
- 18. Модель Кейнса Рассмотрим модель Кейнса зависимости частного потребления С от располагаемого дохода I: С = С0+bI,
- 19. Модель парной линейной регрессии Теоретическая парная линейная регрессионная модель: где β0, β1 − теоретические коэффициенты регрессии,
- 20. Задачи линейного регрессионного анализа Задачи линейного регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным
- 21. Эмпирическое уравнение регрессии По выборке ограниченного объема нельзя точно определить теоретические значения β0 и β1.. Можно
- 22. Эмпирическое уравнение регрессии В результате имеем: где ei – оценка теоретического случайного отклонения εi . Оценки
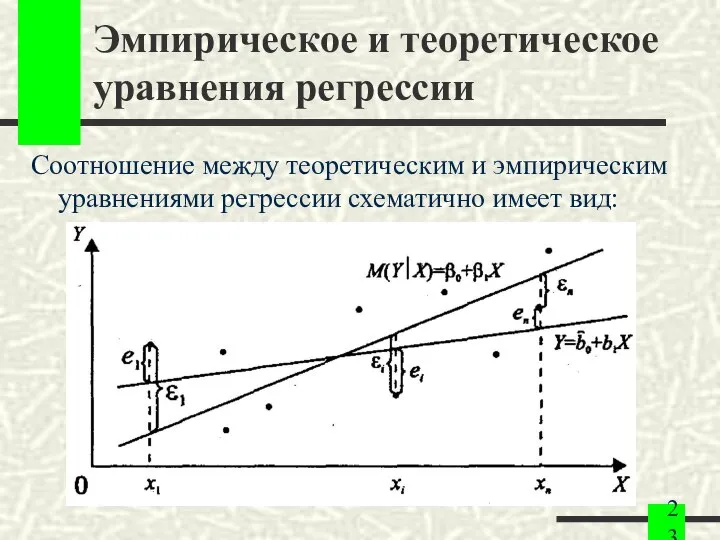
- 23. Эмпирическое и теоретическое уравнения регрессии Соотношение между теоретическим и эмпирическим уравнениями регрессии схематично имеет вид:
- 24. Задача определения коэффициентов регрессии Задача состоит в нахождении по выборке данных оценок b0 и b1 так,
- 25. Метод наименьших квадратов Наиболее распространена методом наименьших квадратов (МНК), реализующий минимизацию суммы квадратов отклонений: Основные особенности
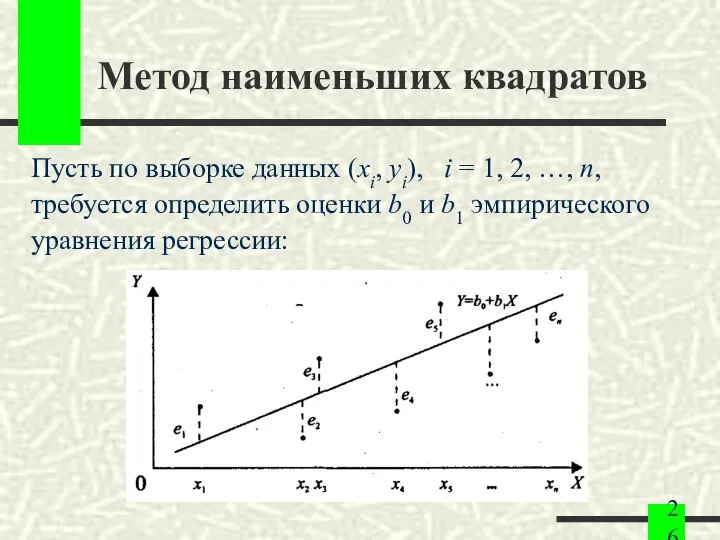
- 26. Метод наименьших квадратов Пусть по выборке данных (xi, yi), i = 1, 2, …, n, требуется
- 27. Метод наименьших квадратов В этом случае минимизируется функция: Т.к. функция Q(b0,b1) непрерывна, выпукла и ограничена снизу,
- 28. Метод наименьших квадратов Приравняем нулю частные производные и затем разделим на n оба уравнения:
- 29. Оценки метода наименьших квадратов Решив последнюю систему уравнений, получим:
- 30. Матричная форма записи МНК эквивалентен ортогональности матрицы Х и вектора е:
- 31. Выводы 1. Оценки МНК являются функциями от выборки, что позволяет их легко рассчитать. 2. Оценки МНК
- 32. Выводы 4. Эмпирическое уравнение регрессии построено так, что 5. Случайные отклонения ei не коррелированы с наблюдаемыми
- 33. Другие методы определения коэффициентов регрессии Другие методы определения коэффициентов регрессии: метод наименьших модулей (МНМ), метод моментов
- 34. Пример (A) построения уравнения регрессии При анализе зависимости объема потребления Y (у.е.) домохозяйства от располагаемого дохода
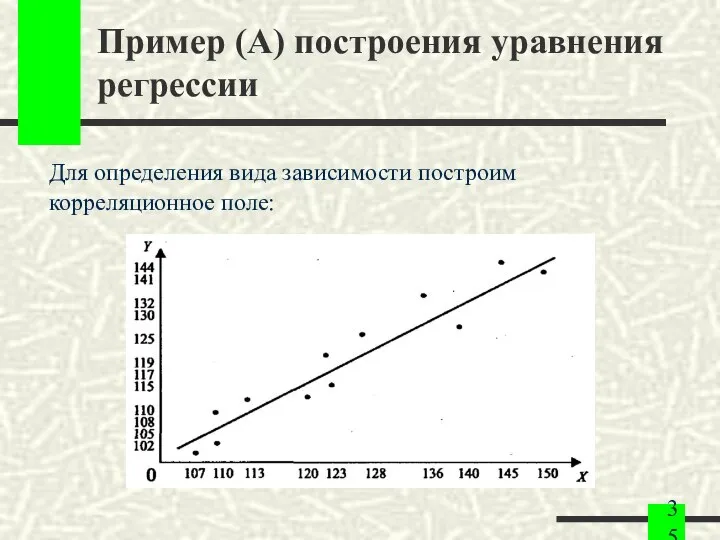
- 35. Пример (A) построения уравнения регрессии Для определения вида зависимости построим корреляционное поле:
- 36. Пример (A) построения уравнения регрессии По расположению точек на корреляционном поле делаем предположение о линейной зависимости:
- 37. Пример (A) построения уравнения регрессии Т.о., уравнение парной линейной регрессии имеет вид: Изобразим данную прямую регрессии
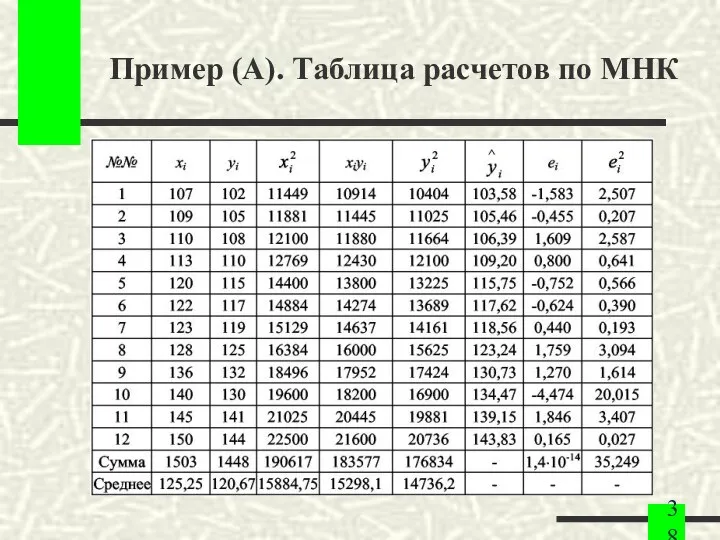
- 38. Пример (A). Таблица расчетов по МНК
- 40. Скачать презентацию





![Регрессионные модели Mx[Y] = ϕ(X) − парная регрессия, Mx[Y] = ϕ(X1,…,Xm)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/647869/slide-7.jpg)


![Регрессионные уравнения Y = M[Y/x] + ε = ϕ(x) + ε](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/647869/slide-10.jpg)






















 Табличные информационные модели
Табличные информационные модели Тригонометрические уравнения
Тригонометрические уравнения Понятие обратной функции
Понятие обратной функции Письменное умножение двух чисел, оканчивающихся нулями
Письменное умножение двух чисел, оканчивающихся нулями Принак подобия треугольников. Урок 33
Принак подобия треугольников. Урок 33 Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3
Нахождение 2 чисел по их сумме и разности (в рыбном царстве). Урок 3 Специальные распределения. χ2 -распределение
Специальные распределения. χ2 -распределение Корреляционный анализ. Парная корреляция
Корреляционный анализ. Парная корреляция Таблица умножения. Тренажер
Таблица умножения. Тренажер Параллельные прямые. Игра "Русское лото"
Параллельные прямые. Игра "Русское лото" Сравнение дробей
Сравнение дробей Парабола и ее применение
Парабола и ее применение Смешанные числа
Смешанные числа Координатная прямая
Координатная прямая Сумма углов треугольника
Сумма углов треугольника Таблица умножения и деления на 2
Таблица умножения и деления на 2 Математическая викторина для 5-6 классов
Математическая викторина для 5-6 классов Методы обработки данных и способы их представления в научном исследовании
Методы обработки данных и способы их представления в научном исследовании Умножение чисел с разными знаками
Умножение чисел с разными знаками Объединение множеств
Объединение множеств Число и цифра 5. Состав числа 5. Сложение и вычитание в пределах 5. Пятиугольник
Число и цифра 5. Состав числа 5. Сложение и вычитание в пределах 5. Пятиугольник История чисел
История чисел Решение задач по теме «Правильный многоугольник»
Решение задач по теме «Правильный многоугольник» Треугольники. Подготовка к ОГЭ. Задание 16
Треугольники. Подготовка к ОГЭ. Задание 16 Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю Построение эскизов кривых в декартовых координатах. (Семинар 3)
Построение эскизов кривых в декартовых координатах. (Семинар 3) Решение игр в смешанных стратегиях
Решение игр в смешанных стратегиях Двугранный угол (ЕГЭ)
Двугранный угол (ЕГЭ)