Содержание
- 2. Вопросы темы Понятие первообразной. Неопределенный интеграл и его свойства. Таблица основных интегралов.
- 3. ПОНЯТИЕ ПЕРВООБРАЗНОЙ
- 4. Определение Функция F(x) называется первообразной функцией для функции f(x) на промежутке X, если в каждой точке
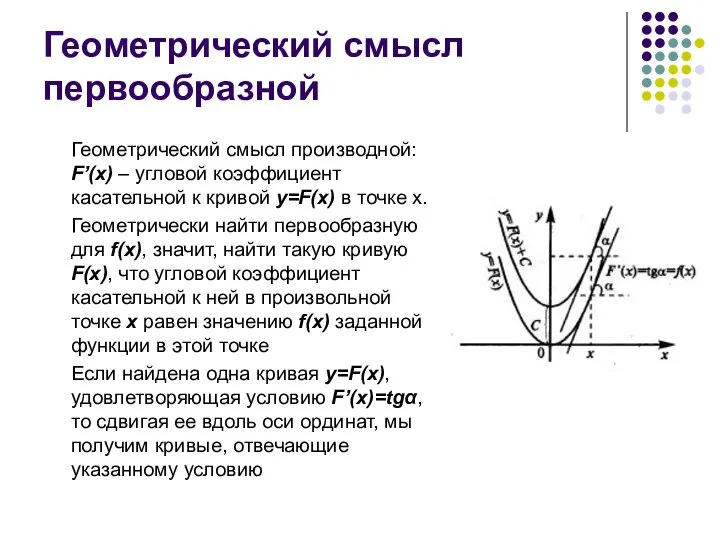
- 5. Геометрический смысл первообразной Геометрический смысл производной: F’(x) – угловой коэффициент касательной к кривой y=F(x) в точке
- 6. Теорема Если F1(x) и F2(x) – первообразные для функции f(x) на промежутке X, то найдется такое
- 7. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
- 8. Определение Совокупность всех первообразных для функции f(x) на промежутке X, называется неопределенным интегралом от функции f(x)
- 9. Свойства неопределенного интеграла Производная от неопределенного интеграла равна подынтегральной функции:
- 10. Свойства неопределенного интеграла Дифференциал неопределенного интеграла равен подынтегральному выражению:
- 11. Свойства неопределенного интеграла Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного
- 12. Свойства неопределенного интеграла Постоянный множитель можно выносить за знак интеграла:
- 13. Свойства неопределенного интеграла Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих
- 14. ТАБЛИЦА ОСНОВНЫХ ИНТЕГРАЛОВ
- 16. НЕКОТОРЫЕ ПОЛЕЗНЫЕ ФОРМУЛЫ ДЛЯ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
- 17. Если , то:
- 18. СПЕЦИАЛЬНЫЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ ИНТЕГРАЛОВ
- 19. Интегрирование методом замены переменной (метод подстановки) Пусть , тогда: где t(x) - дифференцируемая монотонная функция
- 20. Методы замены переменной Если в подынтегральной функции удаётся сразу заметить оба сомножителя, и f(t(x)), и t’(x),
- 21. Методы замены переменной Замену переменной можно осуществлять формальным сведением подынтегрального выражения к новой переменной
- 22. Интегрирование по частям Пусть u(x) и v(x) - функции, имеющие непрерывные частные производные. Тогда по формуле
- 23. Сведение интеграла «к самому себе» С помощью интегрирования по частям (возможно, неоднократного) интеграл выражается через такой
- 24. Рекуррентные соотношения Если подынтегральная функция зависит от некоторого параметра n, и получено соотношение, которое выражает интеграл
- 26. Скачать презентацию














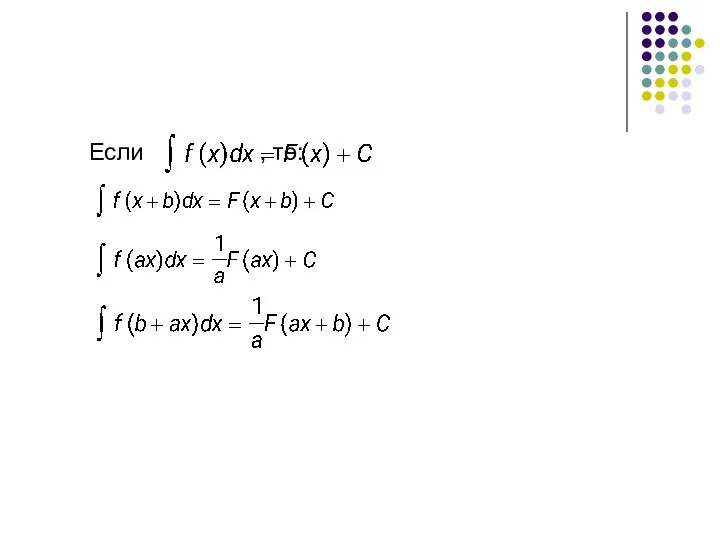







 Сумма углов треугольника
Сумма углов треугольника Позиционные и непозиционные системы счисления
Позиционные и непозиционные системы счисления Упрощение выражений
Упрощение выражений Многогранники. Гимнастика ума
Многогранники. Гимнастика ума Математический диктант
Математический диктант Сравнение смешанных чисел
Сравнение смешанных чисел Роль і місце задач у початковому курсі математики
Роль і місце задач у початковому курсі математики Презентация по математике "тренажер" - скачать бесплатно
Презентация по математике "тренажер" - скачать бесплатно Геометрические тела
Геометрические тела Тест по теме «Объем пирамиды»
Тест по теме «Объем пирамиды» Функции нескольких переменных
Функции нескольких переменных Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости Решение задач с помощью дробно-рациональных выражений 8 класс
Решение задач с помощью дробно-рациональных выражений 8 класс Таблица сложения в пределах 20
Таблица сложения в пределах 20 Занятие по формированию элементарных математических представлений. Тема Насекомые
Занятие по формированию элементарных математических представлений. Тема Насекомые Построение графика квадратичной функции
Построение графика квадратичной функции Зеленая аптека Кузбасса. Проценты
Зеленая аптека Кузбасса. Проценты Bravē režģi
Bravē režģi Введение в теорию оптимизации. Лекция1
Введение в теорию оптимизации. Лекция1 Деление числа на произведение. Деление с остатком на 10, 100, 1000
Деление числа на произведение. Деление с остатком на 10, 100, 1000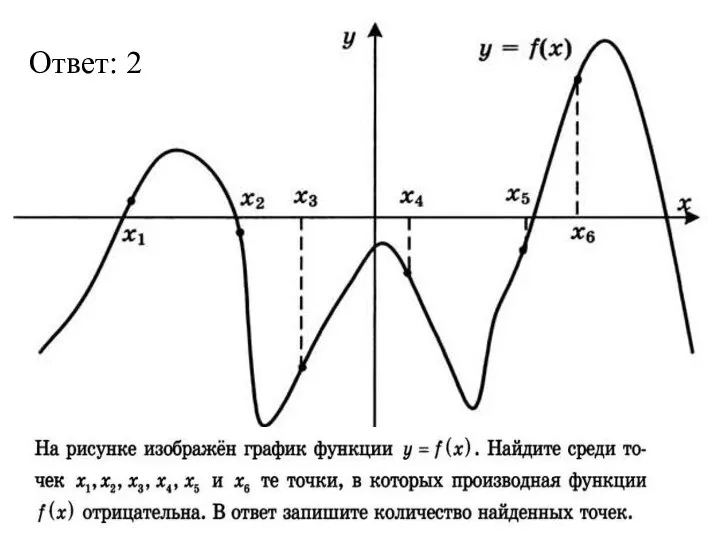 График функции
График функции Алгоритм. Свойства алгоритма
Алгоритм. Свойства алгоритма Алгебра и начало анализа. Функция y=cos x
Алгебра и начало анализа. Функция y=cos x Решение стереометрических задач методом координат
Решение стереометрических задач методом координат Фигуры вращения. Цилиндр. Конус и усечённый конус. Шар и сфера
Фигуры вращения. Цилиндр. Конус и усечённый конус. Шар и сфера Исследование функций с помощью производной
Исследование функций с помощью производной Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда Понятие движения
Понятие движения