Содержание
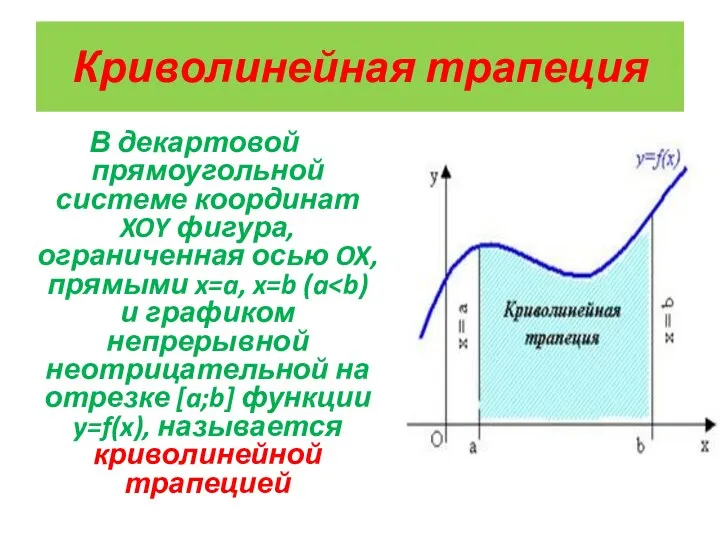
- 2. Криволинейная трапеция В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a
- 3. Для вычисления площади этой фигуры применяется следующая теорема Теорема: Если функция f(x) непрерывна и не отрицательна
- 4. Называется определенным интегралом Числа а и в пределами интегрирования. (нижний, в – верхний)
- 5. Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x),
- 6. Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми
- 7. Замечание: Если функция изменяет знак на промежутке [a;b] , то
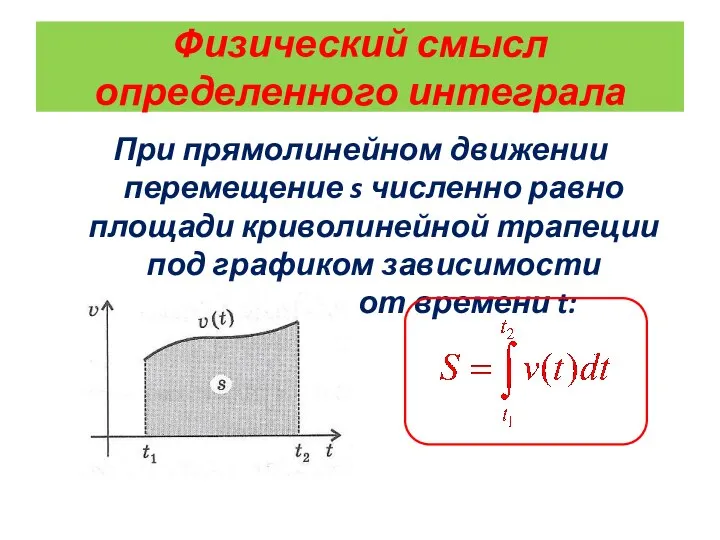
- 8. Физический смысл определенного интеграла При прямолинейном движении перемещение s численно равно площади криволинейной трапеции под графиком
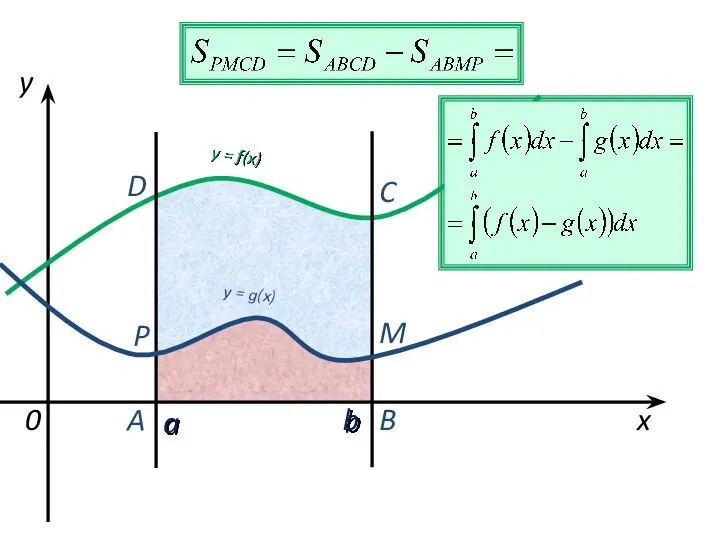
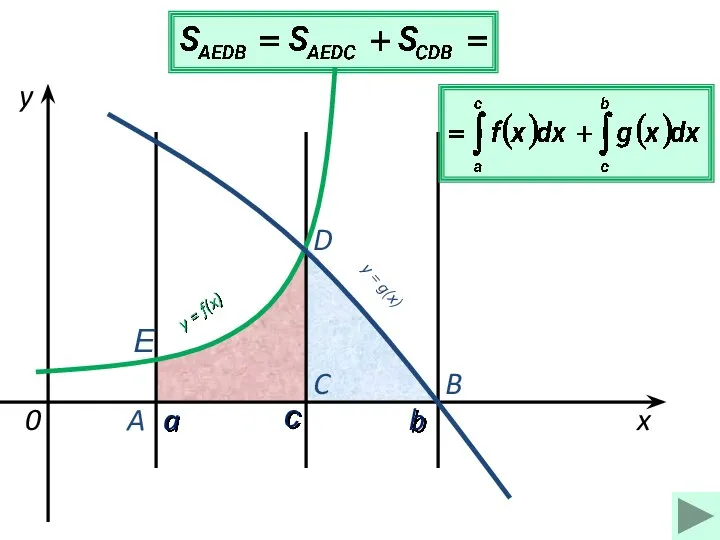
- 9. a b x y y = f(x) 0 y = g(x) A B C D M
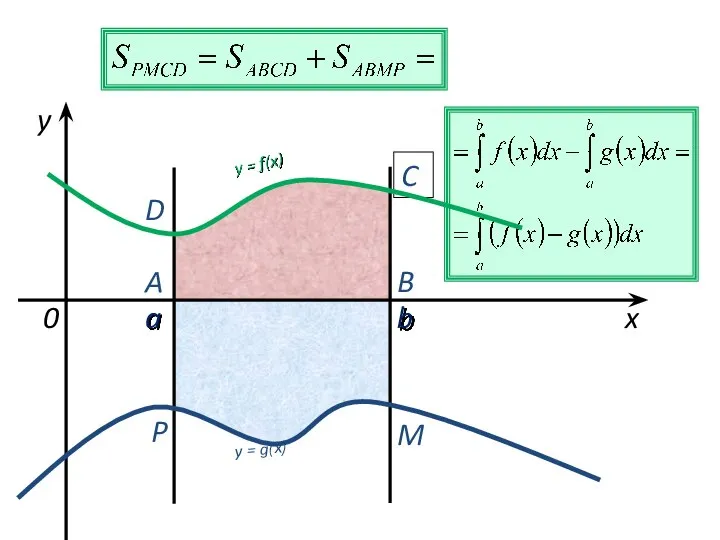
- 10. a b x y y = f(x) 0 y = g(x) A B C D M
- 11. a b x y y = f(x) 0 y = g(x) A B C D с
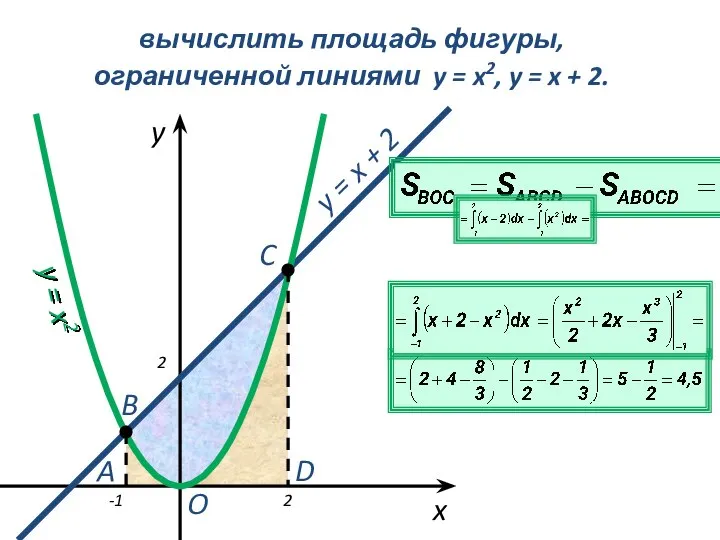
- 12. вычислить площадь фигуры, ограниченной линиями y = x2, y = x + 2. x y y
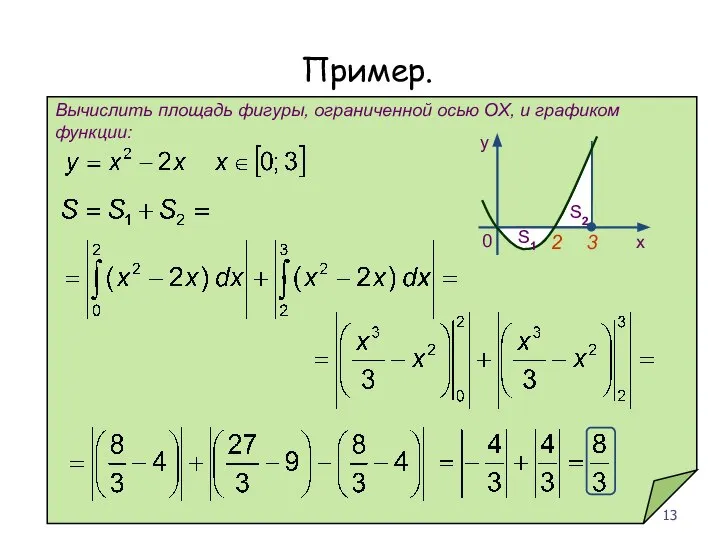
- 13. Пример. Вычислить площадь фигуры, ограниченной осью OX, и графиком функции: 2 3 S1 S2
- 14. Вычисление объема тела вращения Пусть вокруг оси OX вращается криволинейная трапеция, ограниченная непрерывной линией y =
- 16. Скачать презентацию



![Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/743396/slide-5.jpg)
![Замечание: Если функция изменяет знак на промежутке [a;b] , то](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/743396/slide-6.jpg)

 КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку
КАК ЛЮДИ СЧИТАЛИ В СТАРИНУ И КАК ПИСАЛИ ЦИФРЫ Демонстрационный материал к уроку  Степень с рациональным показателем. Степенная функция
Степень с рациональным показателем. Степенная функция Цилиндр. Конус
Цилиндр. Конус Что такое математика?
Что такое математика? Неравенства. Методика систематизации знаний при подготовке к ГИА
Неравенства. Методика систематизации знаний при подготовке к ГИА Первообразные
Первообразные Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости
Задачи по аналитической геометрии на плоскости. Уравнения прямой на плоскости Цель диагностики математического развития детей
Цель диагностики математического развития детей Свойства действий с рациональными числами. Часть 2
Свойства действий с рациональными числами. Часть 2 Предварительный эксперимент и методы его анализа
Предварительный эксперимент и методы его анализа Презентация на тему Скорость сближения и удаления
Презентация на тему Скорость сближения и удаления  Разбор задач
Разбор задач Действия над комплексными числами в алгебраической форме
Действия над комплексными числами в алгебраической форме Математика 1 класс
Математика 1 класс  Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний
Арифметическая и геометрическая прогрессии. Урок обобщения и систематизации знаний Повтарение по математике. Уравнение
Повтарение по математике. Уравнение Презентация по математике "Математика – гимнастика ума" - скачать бесплатно
Презентация по математике "Математика – гимнастика ума" - скачать бесплатно Реляционная алгебра. Операторы
Реляционная алгебра. Операторы Связь математики с биологией
Связь математики с биологией Комбинаторика. 5 класс
Комбинаторика. 5 класс Аттестационная работа. Методическая разработка по выполнению проекта Геометрия на клетчатой решетке
Аттестационная работа. Методическая разработка по выполнению проекта Геометрия на клетчатой решетке Параллельные алгоритмы вычислительной алгебры. Разделение переменных
Параллельные алгоритмы вычислительной алгебры. Разделение переменных Математика в педиатрии Выполнила:
Математика в педиатрии Выполнила:  Формула площади прямоугольника. Математика повсюду, Глазом только поведёшь – И примеров разных уйму, Где применить её найдё
Формула площади прямоугольника. Математика повсюду, Глазом только поведёшь – И примеров разных уйму, Где применить её найдё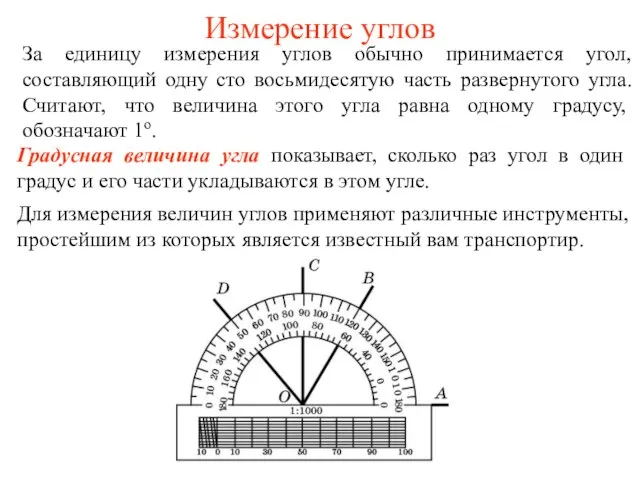 Измерение углов. Вопросы, упражнения
Измерение углов. Вопросы, упражнения Презентация по математике "Логические задачи 1 класс" - скачать бесплатно
Презентация по математике "Логические задачи 1 класс" - скачать бесплатно Тригонометрические уравнения
Тригонометрические уравнения Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения
Линейная алгебра. Невырожденные матрицы. Обратная матрица. Матричные уравнения