Понятие многогранника. Призма

Определение

Многогранником называется поверхность, которая составлена из многоугольников и ограничивает некоторое геометрическое

Выпуклый многогранник

Невыпуклый многогранник

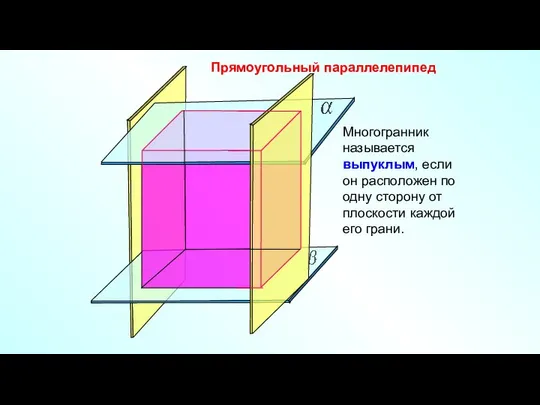
Прямоугольный параллелепипед

Многогранник называется выпуклым, если он расположен по одну сторону от

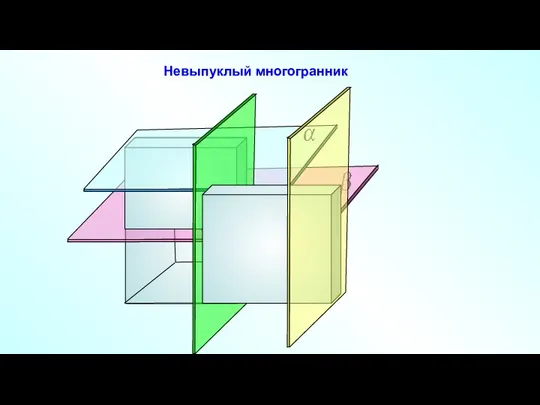
Невыпуклый многогранник

φ1

φ2

φ3

φ3

φ2

φ1

φ1 + φ2 + φ3 < 360°

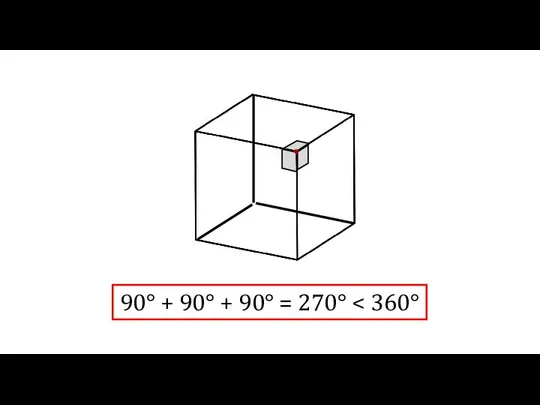
90° + 90° + 90° = 270° < 360°

Тетраэдр

Куб

Октаэдр

Додекаэдр

Икосаэдр

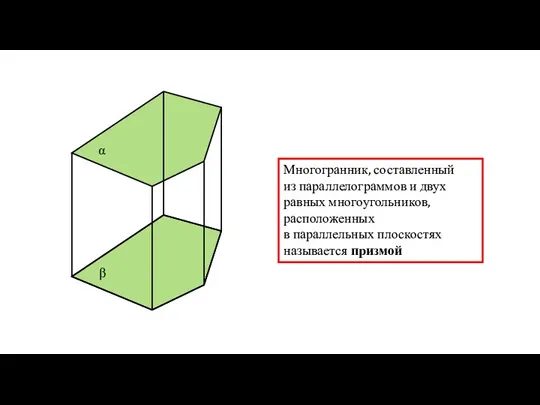
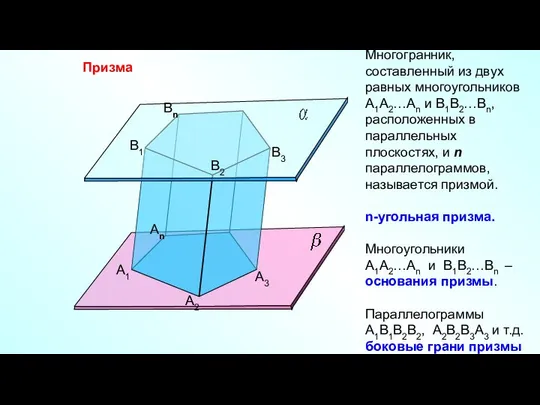
α

β

Многогранник, составленный
из параллелограммов и двух равных многоугольников, расположенных
в параллельных

Призма

А1

А2

Аn

B1

B2

Bn

B3

А3

Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в

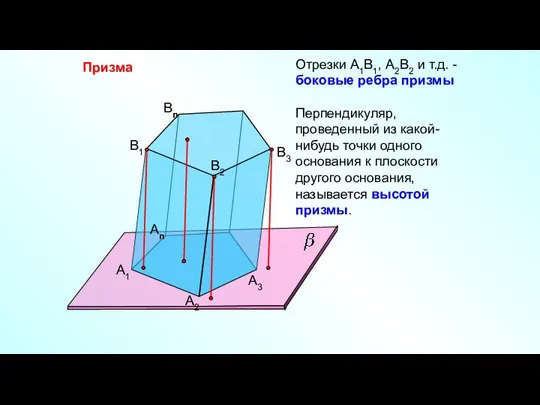
Призма

А1

А2

Аn

B1

B2

Bn

B3

А3

Отрезки А1В1, А2В2 и т.д. -
боковые ребра призмы
Перпендикуляр, проведенный из

Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в

A1

B1

C1

A

B

C

основания

боковая грань

боковое ребро

АВСA1B1C1 — треугольная призма

высота

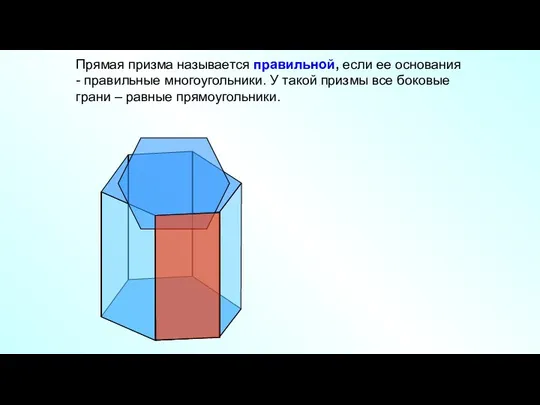
Прямая призма называется правильной, если ее основания - правильные многоугольники. У

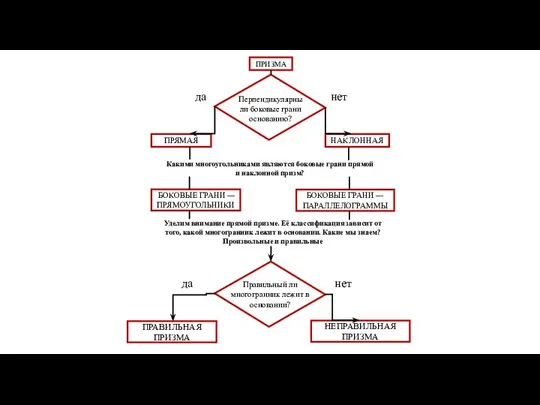
ПРИЗМА

ПРЯМАЯ

НАКЛОННАЯ

Какими многоугольниками являются боковые грани прямой и наклонной призм?

БОКОВЫЕ ГРАНИ —

Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью

О.

О.

Б.Г.

Б.Г.

Б.Г.

— основания

— боковые грани

Sполн. = Sбок. + 2Sосн.

Сумма площадей всех граней

Теорема

Площадь боковой поверхности прямой призмы равна произведению высоты призмы на периметр

Задача 2

АВСDА1В1С1D1 — прямой параллелепипед

Дано:

АС = 24 см

ВD = 10 см

Найти:

Задача 1

АВСА1В1С1 — прямая треугольная призма

Дано:

∠ВА1С = 30°

А1В = 10,

Решение:

1)

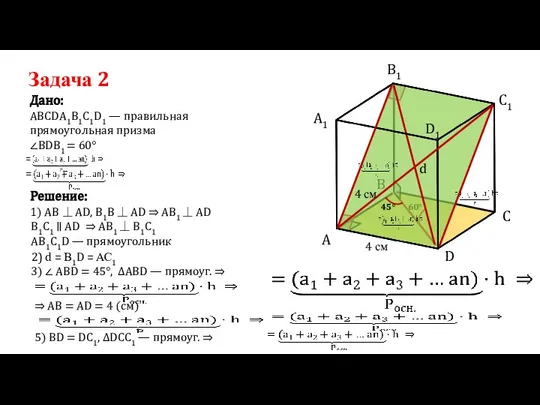
Задача 2

АВСDА1В1С1D1 — правильная прямоугольная призма

Дано:

Решение:

1) AB ⏊ AD, B1B ⏊