Небесная механика

Законы Кеплера

•

Первый закон Кеплера… и длина эллипса

Параметрическое уравнение эллипса

x acos
y bsin

Длина

Гравитационный потенциал
Материальной точки

•
•

GM
r





Сферической оболочки





GM
r
GM
a




, ra




Sph









,

ra







Внутри сферической оболочки пробная частица находится в

Притяжение пробной частицы внутри сферы:
элементарные соображения

Телесный угол

d dS r1

 dS r2

2

2

1

2

2
2
F

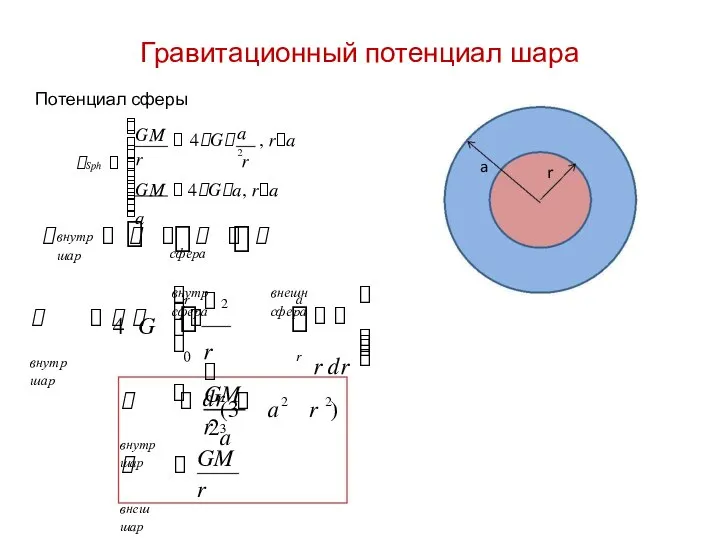
Гравитационный потенциал шара

Потенциал сферы






GM
r
GM
a

a
2



4G , ra






r

Sph





a

r






 4Ga, ra
 
внутр внешн
сфера сфера













Гравитационный потенциал шара
Теорема Дирихле






4G, внутри объема
вне объема


















2

c
1
r

out




1




  

ra



out

c2

r

 0









 

Гравитационный потенциал шара

out

inner ra

Учитываем сшивку на границе
потенциала и силы

ra

out

inner



ra

ra

Потенциал шара





GM
r




, ra




шар









GM

(3
a3

a

Гравитационный потенциал

•
•

Интегрирование по объему
Суммирование по элементарным
составляющим

•

Теорема Дирихле

Сфера, цилиндр, шар….

Гравитационный потенциал эллипсоида

Теорема Лапласа
Однородные софокусные эллипсоиды притягивают внешнюю точку с силами,
одинаково

Задача Эйлера о двух неподвижных массах

•
•

Гравитационный потенциал сжатого
сфероида эквивалентен потенциалу
стержня мнимой

Разложение потенциала в ряд Лапласа

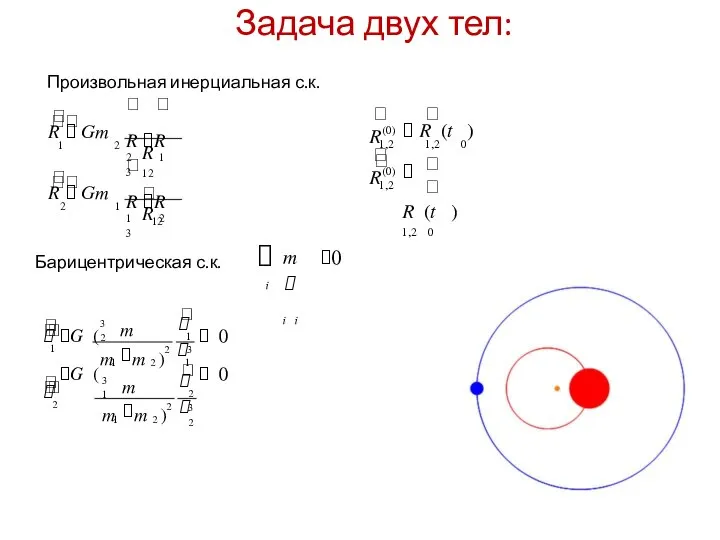
Задача многих тел

•

Произвольная инерциальная с.к.

 





(0)

R R (t )





R R





N
R G

Задача двух тел:

Произвольная инерциальная с.к.

 
R R
2 1
3









R  Gm

R

(0)

 R

Задача двух тел

Относительная система координат


r







rG(Mm)  0

r

3





r

(0)
(0)

 r(t )

0









r

 r(t )

0

Первые

Задача двух тел. Интеграл Лапласа

rI
r3




G(M m)
 





rI

 0

Интеграл Лапласа













r



вектор Лапласа

rI 

r

Уравнения

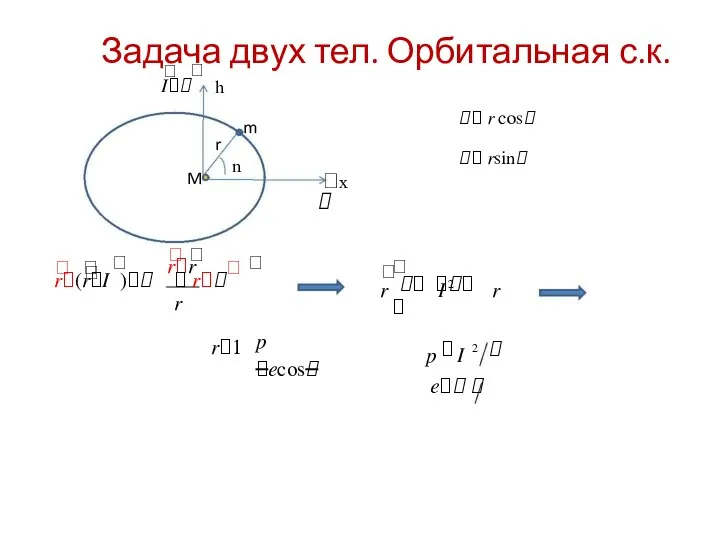
Задача двух тел. Орбитальная с.к.





I

h




 r cos
 rsin

m

r

n

M

x















rr










r(rI )  r

r



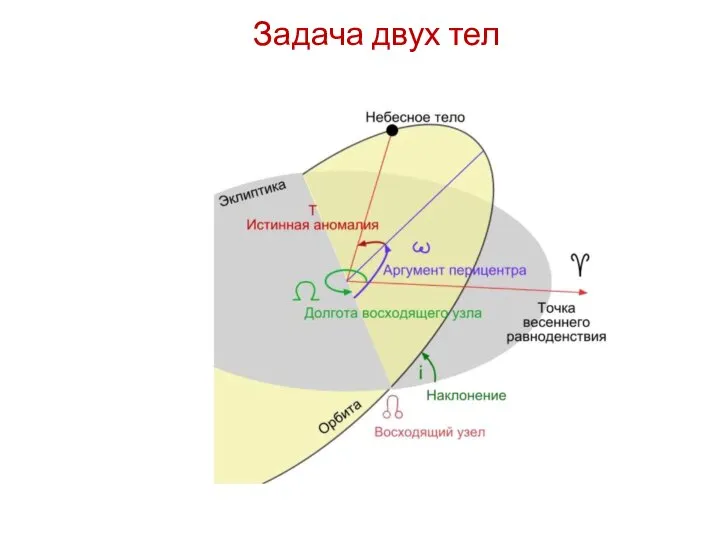
Задача двух тел

Уравнение Кеплера

n

 (t )
3/2
ecos ) p

dn

r2

n  I





(1

n

2

0

n 1e E
tg 

tg
1e

Смещение перигелия Меркурия

Ньютоновское приближение

rg  2

GM

2



du 
dn 

2GMm

2

Em
u 



u

2








c

2

I

2

I
2

Релятивистская задача

2

rgmc2



du 
d

Задача трех тел




2







r

2 r

r

1

1

3

3

r

r

1

2



U

x2ny





1,2

Gm1,2



x
U

y2nx







y

n

2

 

U(x, y,z)

2 (x2

  

y

)



U

2

1
r r
1

2


z



z

2





2

V 2U

Задача трех тел




J

n

2

 

2

V 2U C

U(x, y,z) (x

 y

) 

2

2

1

2

2

r r

1

2

Поверхности

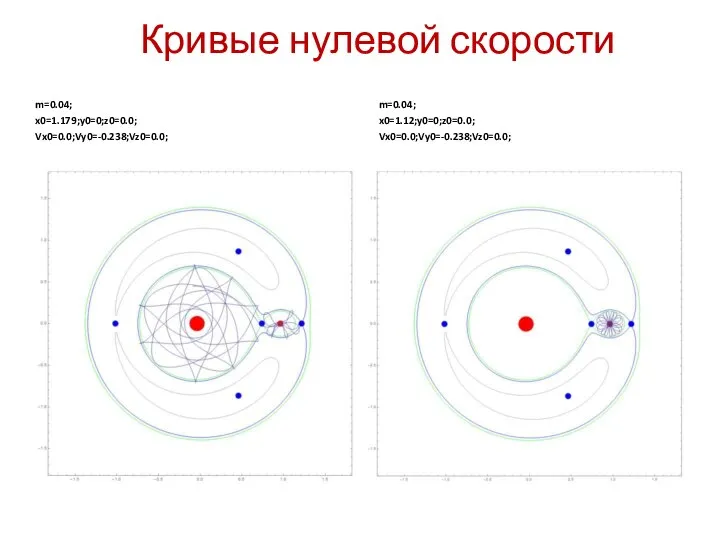
Кривые нулевой скорости

m=0.04;
x0=1.179;y0=0;z0=0.0;
Vx0=0.0;Vy0=-0.238;Vz0=0.0;

m=0.04;
x0=1.12;y0=0;z0=0.0;
Vx0=0.0;Vy0=-0.238;Vz0=0.0;

Точки Лагранжа

L4,L5

x1/ 22
y 3 / 2

r  r 1

1

2

2

1

L1,L2

1/3









2
31

r
2



L3

2

7
12 1

 

Семейство Хильды

Резонанс 3:2
L3,L4,L5 – афелии астероидов

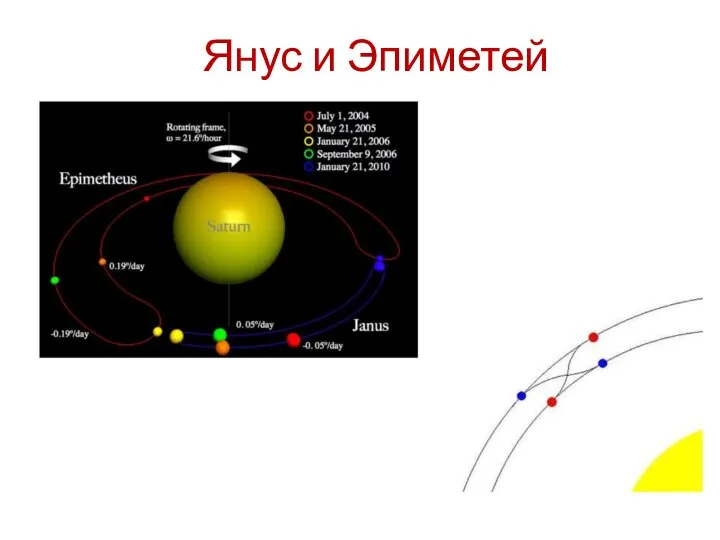
Янус и Эпиметей

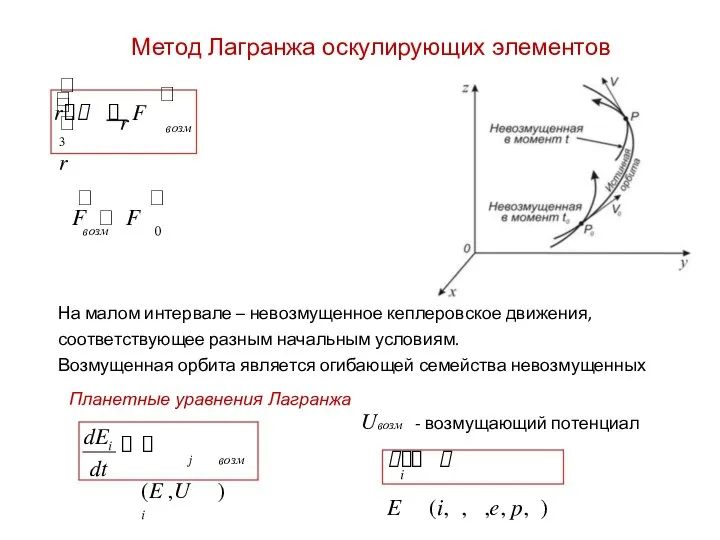
Метод Лагранжа оскулирующих элементов


 r
3
r







r  F

возм





F  F

возм

0

На малом интервале

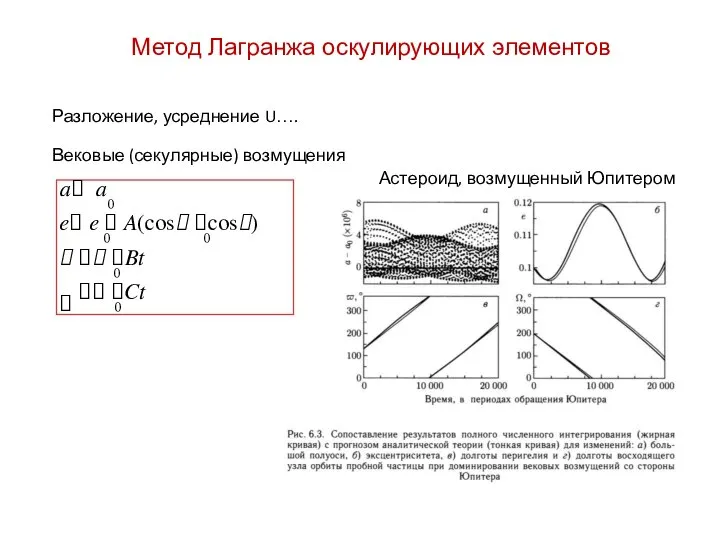
Метод Лагранжа оскулирующих элементов

Разложение, усреднение U….

Вековые (секулярные) возмущения

Астероид, возмущенный Юпитером

a a

0

e

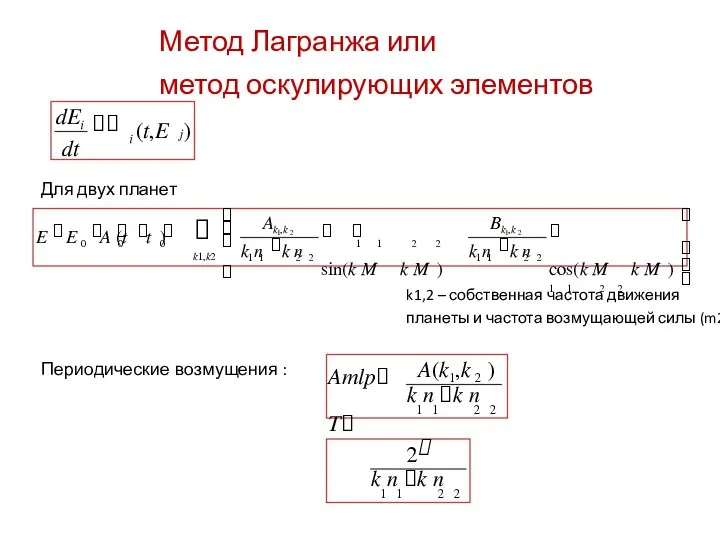
Метод Лагранжа или
метод оскулирующих элементов

dE



(t,E j)

i

i

dt

Для двух планет








A

B







   



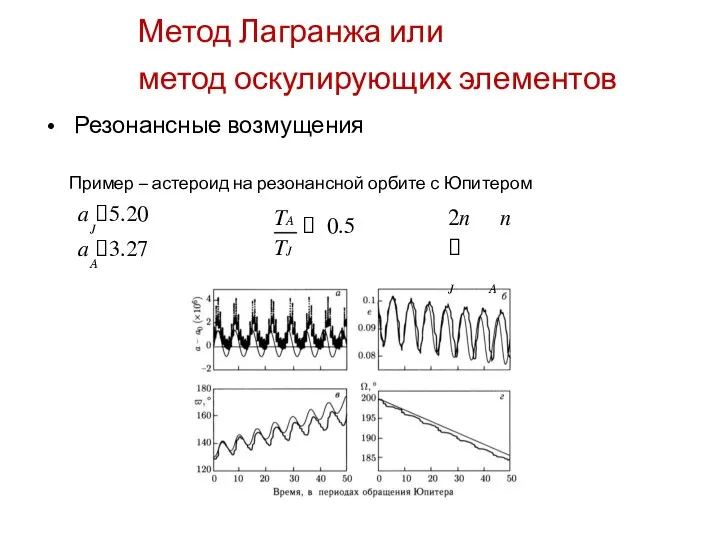
Метод Лагранжа или
метод оскулирующих элементов

•

Резонансные возмущения

Пример – астероид на резонансной орбите

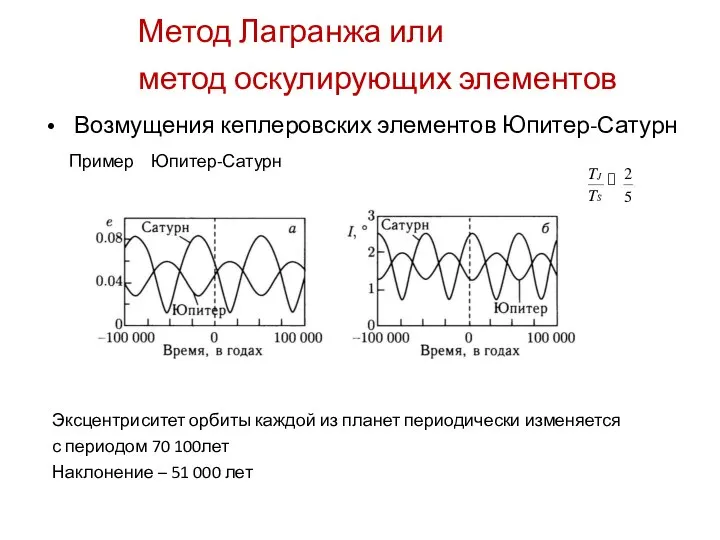
Метод Лагранжа или
метод оскулирующих элементов

•

Возмущения кеплеровских элементов Юпитер-Сатурн

Пример Юпитер-Сатурн

TJ
TS

2



5

Эксцентриситет орбиты каждой

Метод Лагранжа или
метод оскулирующих элементов

A(k ,k )

Amlp

1

2

•

Короткопериодические возмущения

k n k n

1

1

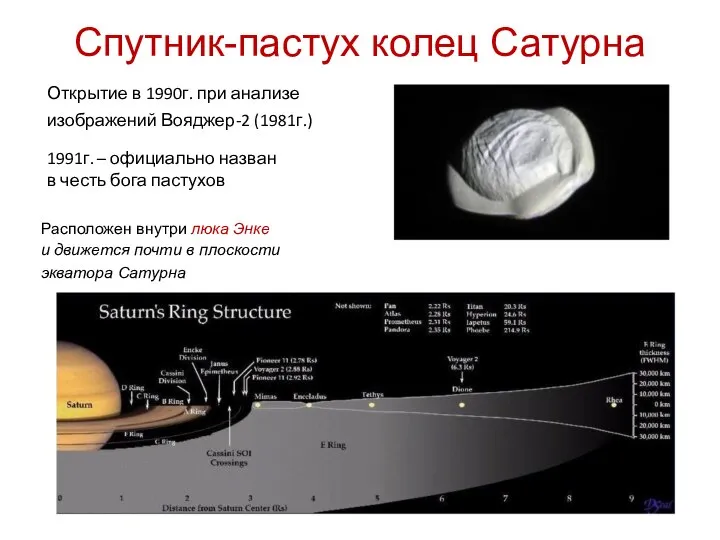
2

Спутник-пастух колец Сатурна

Открытие в 1990г. при анализе
изображений Вояджер-2 (1981г.)

1991г.

– официально назван

в

Спутник-пастухи Сатурна

Прометей (внутренний)
Пандора (внешний)

Cassini image

Спутники-пастухи

Cassini's confirmation that a small moon orbits within the Keeler gap

Гиперион (спутник перевертыш)

Двуликий… Япет

Cassini images

Спин-орбитальный резонанс

Астероид Круитни

Орбитальный резонанс с Землей 1:1

Сопутствующая ситема к.

Проекция на эклиптику

Сечение Пуанкаре

Сечение (отображение) Пуанкаре – отображение проекции
траектории на выделенную плоскость фазового

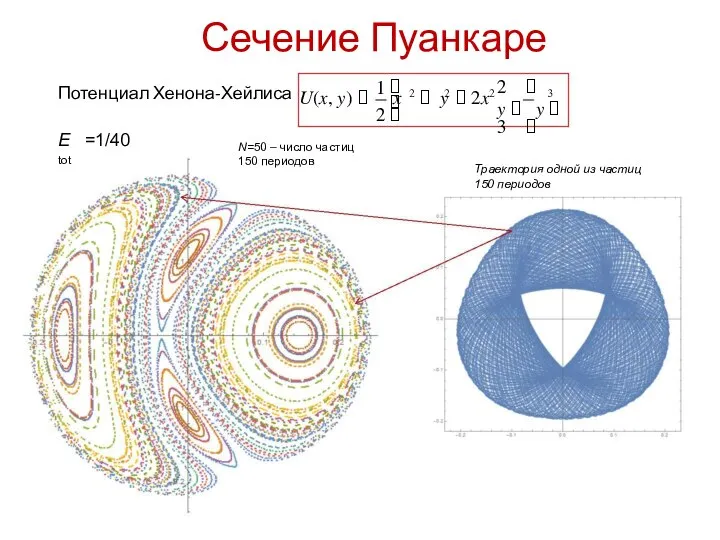
Сечение Пуанкаре

1




2 
y  y
3 

Потенциал Хенона-Хейлиса

U(x, y)  x

2

 y

2



Сечение Пуанкаре

Потенциал Хенона-Хейлиса

1 
U(x, y)  x

2 
y  y
3 

2



Сечение Пуанкаре

1




2 
y  y
3 

Потенциал Хенона-Хейлиса

U(x, y)  x

2

 y

2

2x

2

3




2

E

Сечение Пуанкаре

1




2 
y  y
3 

Потенциал Хенона-Хейлиса

U(x, y)  x

2

 y

2

2x

2

3




2

E

Сечение Пуанкаре

1




2 
y  y
3 

Потенциал Хенона-Хейлиса

U(x, y)  x

2

 y

2

2x

2

3




2

E