Содержание
- 2. Тайны планетных орбит. Древнегреческие учёные умели решать немногие задачи кинематики – рассчитать либо равномерное прямолинейное движение,
- 3. В конце 17 века Исаак Ньютон открыл законы динамики, сформулировал закон всемирного тяготения и развил математические
- 4. Он также развил новое исчисление, которое оказалось по сути дела тождественным построенному Ньютоном. Обозначения, введённые Лейбницем,
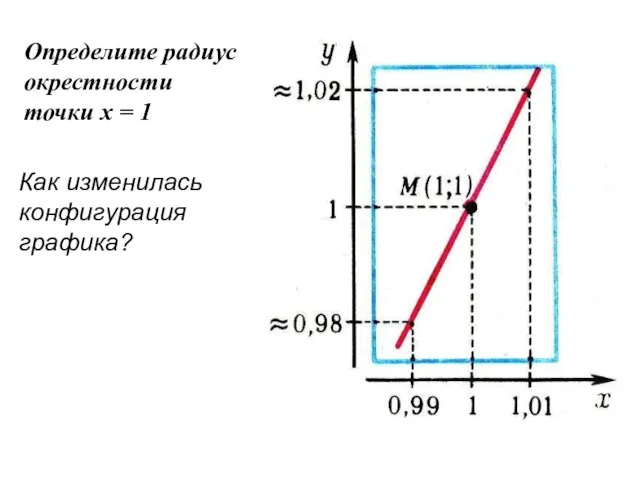
- 5. Рассмотрим график функции вблизи точки М(1;1), изображённый в разных масштабах.
- 6. Как изменилась конфигурация графика?
- 7. Определите радиус окрестности точки х = 1 Как изменилась конфигурация графика?
- 8. Основные выводы 1. Чем крупнее масштаб, тем меньше график функции будет отличаться от некоторой прямой, проходящей
- 9. Cвойство «линейности в малом». Выразим это свойство на языке формул. Как перевести на математический язык слова
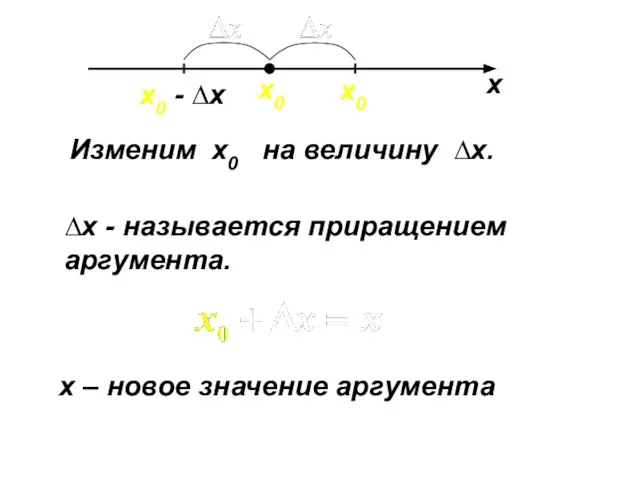
- 10. х х0 Изменим x0 на величину ∆x. ∆x - называется приращением аргумента. x0 + ∆x x0
- 11. Величина y(x) – y(x0) называется приращением функции в точке x0 и обозначается ∆y(x0) .
- 12. Таким образом, чтобы вычислить приращение функции f(x) при переходе от точки x0 к точке x =
- 13. Определение Функция y = f(x) называется дифференцируемой в точке x0 , если её приращение в этой
- 14. Что такое коэффициент А?
- 15. Значит, где - б. м. ф. при по определению предела функции в точке. Выразим из равенства
- 16. Определение Производной функции y = f(x) в точке x0 называется предел отношения приращения функции в точке
- 17. Рассмотрим пример из физики, который также приводит к понятию производной.
- 18. Пусть тело движется по закону Надо найти скорость движения на промежутке времени Если то
- 19. Используя определение, найдите производные функций в точке :
- 20. Чтобы найти производную функции в точке, надо: найти приращение функции в точке ; найти отношение приращения
- 21. Найдите производные следующих функций в точке :
- 23. Скачать презентацию


















 Задачи на доли и дроби
Задачи на доли и дроби Конформные отображения
Конформные отображения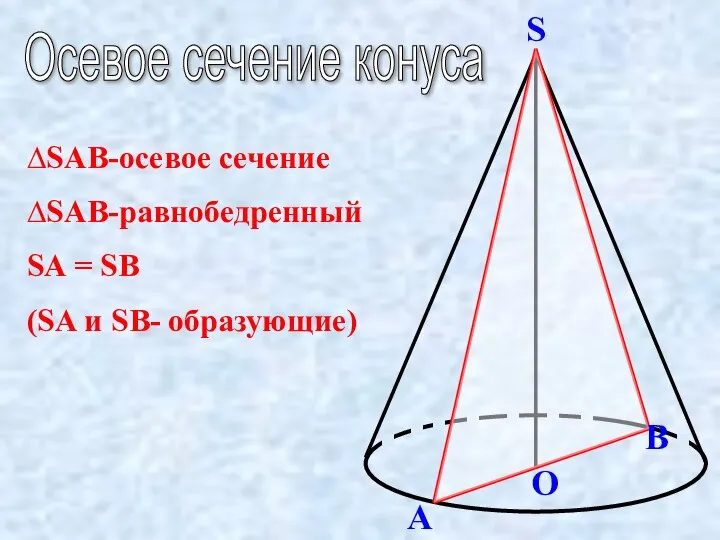 Осевое сечение конуса и цилиндра
Осевое сечение конуса и цилиндра Сложение отрицательных чисел
Сложение отрицательных чисел Теорема о трех перпендикулярах. Решение задач
Теорема о трех перпендикулярах. Решение задач Диагностическая работа по математике (октябрь)
Диагностическая работа по математике (октябрь) Решение уравнений, неравенств и их систем с модулями, 9 класс
Решение уравнений, неравенств и их систем с модулями, 9 класс Неопределенный интеграл. Определения и теоремы
Неопределенный интеграл. Определения и теоремы Квадратный трехчлен. Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлен
Квадратный трехчлен. Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлен Вводное повторение.Геометрия 8 класс
Вводное повторение.Геометрия 8 класс Измерение отрезков
Измерение отрезков Задачи по геометрии. (9 класс)
Задачи по геометрии. (9 класс) Раскраска графа
Раскраска графа Математика. 3 класс
Математика. 3 класс Паралельне проектування
Паралельне проектування Софизмы и парадоксы
Софизмы и парадоксы Состав числа 8
Состав числа 8 Задачи по теории вероятностей
Задачи по теории вероятностей  Метод координат как универсальный способ решения заданий С-2 ЕГЭ по математике
Метод координат как универсальный способ решения заданий С-2 ЕГЭ по математике Стереометрия. Построение сечений многогранников
Стереометрия. Построение сечений многогранников Треугольники и их виды. Практическая работа № 1
Треугольники и их виды. Практическая работа № 1 Параллельные и перпендикулярные прямые
Параллельные и перпендикулярные прямые Построение сечений параллелепипеда
Построение сечений параллелепипеда Неразрешимость исчисления предикатов
Неразрешимость исчисления предикатов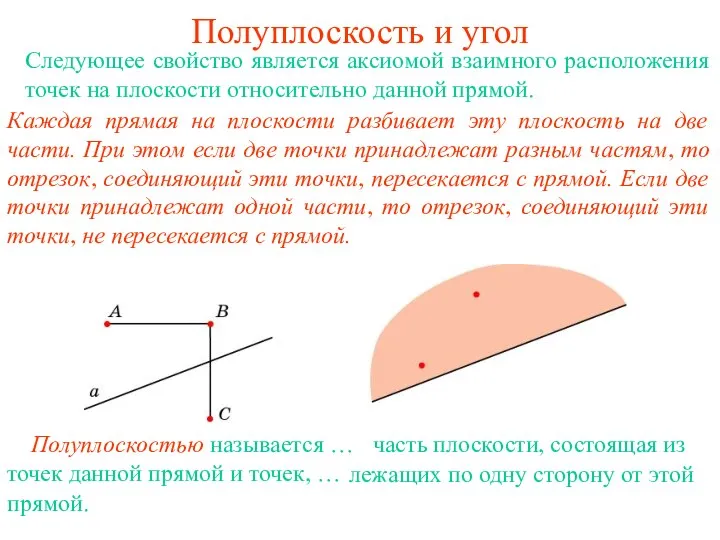 Полуплоскость и угол
Полуплоскость и угол Математический марафон по теме «Квадратные уравнения»
Математический марафон по теме «Квадратные уравнения» Дифференциальное исчисление
Дифференциальное исчисление Командное задание. Численное интегрирование
Командное задание. Численное интегрирование