Содержание
- 2. Производной функции в точке называется предел, если он существует и конечен, отношения приращения функции к соответствующему
- 3. Производная
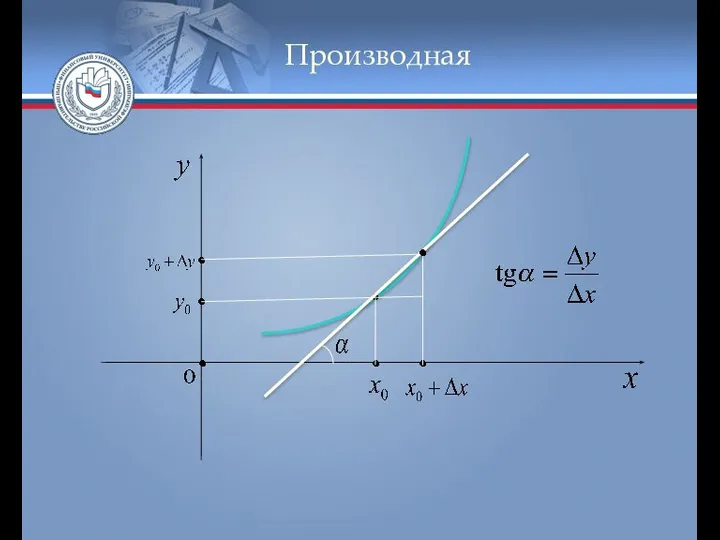
- 4. Производная Геометрический смысл производной функции: производная функции в точке равна тангенсу угла наклона касательной, проведённой к
- 5. Производная Нахождение производной функции называется дифференцированием функции. Критерий дифференцируемости функции в точке: Чтобы функция была дифференцируемой
- 6. Теорема (Необходимое условие дифференцируемости функции): Если функция дифференцируема в некоторой точке, то она в этой точке
- 7. Правила дифференцирования Пусть С - постоянная величина, 1. 2. 3. 4. 5.
- 8. Формулы дифференцирования
- 9. Формулы дифференцирования
- 10. Производная Производная сложной функции При условии, что функции имеют производные в соответствующих точках.
- 11. Задача Пример. Найти производную функции
- 12. Задача Пример. Найти производную функции Ответ:
- 13. Задача Пример. Найти производную функции
- 14. Задача Пример. Найти производную функции Ответ:
- 15. Задача Пример. Найти производную функции
- 16. Задача Ответ:
- 17. Задача Написать уравнение касательной к графику функции в точке его пересечения с осью ординат.
- 18. Задача Решение:
- 19. Задача Написать уравнение касательной к графику функции перпендикулярной прямой Решение:
- 20. Эластичностью функции называется предел отношения относительного приращения функции к относительному приращению переменной, когда приращение этой переменной
- 21. Эластичность Из определения вытекает формула расчёта эластичности функции:
- 22. Эластичность Эластичность функции приближённо показывает на сколько процентов изменится функция при изменении независимой переменной на 1%.
- 23. Свойства эластичности Эластичность функции равна произведению независимой переменной на темп изменения функции
- 24. Свойства эластичности 3. Эластичности взаимно обратных функции являются взаимно обратными:
- 25. Задача Пример. Зависимость между себестоимостью единицы продукции y (тыс.руб.) и выпуском продукции х (млн.руб.) выражается функцией
- 26. Задача Решение: Получили то, что при выпуске продукции, равном 150 млн.руб. увеличение этого выпуска на 1%
- 27. Производная Основные теоремы дифференциального исчисления: 1. Теорема Ферма. Если дифференцируемая на множестве функция достигает наибольшего или
- 28. Производная 2. Теорема Ролля. Пусть функция непрерывна на некотором отрезке, дифференцируема внутри отрезка и на концах
- 29. Производная 3. Теорема Лагранжа. Пусть функция непрерывна на некотором отрезке [a; b], дифференцируема внутри отрезка (на
- 30. Производная 4. Теорема Ферма. Пусть функции непрерывны на некотором отрезке [a; b], дифференцируемы на интервале (a;
- 31. Правило Лопиталя Применяется при вычислении пределов для устранения неопределённостей видов
- 32. Правило Лопиталя
- 33. Задача Пример. Найти
- 34. Задача Пример. Найти Решение:
- 35. Задача Пример. Найти
- 36. Задача Пример. Найти Решение:
- 37. Задача Пример. Найти
- 38. Задача Пример. Найти Решение:
- 39. Производная Достаточные признаки монотонности функции: Если во всех точках некоторого множества производная дифференцируемой функции положительна, то
- 40. Производная 3. Если во всех точках некоторого множества производная дифференцируемой функции равна нулю, то функция на
- 41. Точка является точкой максимума функции , если найдётся такая окрестность этой точки, во всех точках которой
- 42. Точка является точкой минимума функции , если найдётся такая окрестность этой точки, во всех точках которой
- 43. Экстремум Необходимое условие существования экстремума функции в точке: Если в некоторой точке дифференцируемая функция достигает экстремума,
- 44. Экстремум Достаточные условия существования экстремума функции в точке: 1. Если найдётся такая окрестность критической точки, во
- 45. Экстремум Если функция дважды дифференцируема в некоторой точке и в этой точке производная первого порядка равна
- 46. Экстремум Для отыскания наибольшего и наименьшего значений функции на отрезке следует: Найти производную функции Найти критические
- 47. Задача Пример. Найти наибольшее и наименьшее значения функции на отрезке [-2; 0,5]. Решение:
- 48. Задача Пример. Найти наибольшее и наименьшее значения функции на отрезке [-2; 0,5]. Решение:
- 49. Функция называется выпуклой вниз (или вогнутой) на множестве, если для любых двух значений из ООФ выполняется
- 50. Функция называется выпуклой вверх (или выпуклой) на множестве, если для любых двух значений из ООФ выполняется
- 51. Производная Теорема. Функция вогнута на множестве тогда и только тогда, когда её первая производная на этом
- 52. Производная Теорема (достаточное условие перегиба функции). Если вторая производная дважды дифференцируемой функции при переходе через некоторую
- 54. Скачать презентацию












































![Задача Пример. Найти наибольшее и наименьшее значения функции на отрезке [-2; 0,5]. Решение:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1460712/slide-46.jpg)
![Задача Пример. Найти наибольшее и наименьшее значения функции на отрезке [-2; 0,5]. Решение:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1460712/slide-47.jpg)




 Степень с рациональным показателем. Степенная функция
Степень с рациональным показателем. Степенная функция Возникновение геометрии
Возникновение геометрии Арифметический квадратный корень
Арифметический квадратный корень Преобразование графиков функции
Преобразование графиков функции Презентация по математике "Решение задач обязательной части ГИА" - скачать бесплатно
Презентация по математике "Решение задач обязательной части ГИА" - скачать бесплатно Взаимное пересечение поверхностей
Взаимное пересечение поверхностей Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Задачи на нахождение слагаемого и суммы
Задачи на нахождение слагаемого и суммы Длина окружности и площадь круга
Длина окружности и площадь круга Корреляционный анализ. Оценка коэффициента корреляции
Корреляционный анализ. Оценка коэффициента корреляции Задачи на деление
Задачи на деление Логарифм. Основные свойства логарифмов
Логарифм. Основные свойства логарифмов Численное решение обыкновенных дифференциальных уравнений
Численное решение обыкновенных дифференциальных уравнений Подобные треугольники
Подобные треугольники Сложение и вычитание десятичных дробей Урок-путешествие
Сложение и вычитание десятичных дробей Урок-путешествие  Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения
Уравнения и неравенства с одной переменной. Урок разноуровнего обобщающего повторения Презентация по математике "Площадь Единицы площади" - скачать
Презентация по математике "Площадь Единицы площади" - скачать  Формализованное представление ЭА при автоматизированном проектировании
Формализованное представление ЭА при автоматизированном проектировании Решение задач на перпендикулярность прямой и плоскости
Решение задач на перпендикулярность прямой и плоскости Решение задач с помощью линейных уравнений
Решение задач с помощью линейных уравнений Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Смешанные числа
Смешанные числа Округление чисел Артамонова Лариса Владимировна, учитель математики МКОУ «Москаленский лицей»
Округление чисел Артамонова Лариса Владимировна, учитель математики МКОУ «Москаленский лицей» Правильные многогранники
Правильные многогранники Прямоугольник. Виды прямоугольников
Прямоугольник. Виды прямоугольников Третий признак равенства треугольников
Третий признак равенства треугольников Область определения функции
Область определения функции Презентация по математике "Деление дробей" - скачать
Презентация по математике "Деление дробей" - скачать