Содержание
- 2. Определения и теоремы: Определение. Первообразной функцией для данной функции f(x) на данном промежутке называется, такая функция
- 3. Теорема. Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от
- 4. Определение. Общее выражение для всех первообразных данной непрерывной функции f(x) называется неопределенным интегралом от функции f(x)
- 5. Свойства неопределенного интеграла 1.Если непрерывно дифференцируемая функция, то 2.
- 6. 3. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме неопределенных интегралов от
- 7. 2.Таблица простейших неопределенных интегралов Таблица интегралов
- 8. 1. 2.
- 9. 5. 4. 3.
- 10. 7. 8. 6.
- 11. 10. 9.
- 12. Дополнительные формулы: 1. 2.
- 13. 3. 4. 5.
- 14. 3.Основные методы интегрирования : 1.Метод разложения. , тогда Пусть
- 15. 2.Метод подстановки (метод введения новой переменной)
- 16. 3.Метод интегрирования по частям.
- 17. Неберущиеся интегралы
- 19. Скачать презентацию






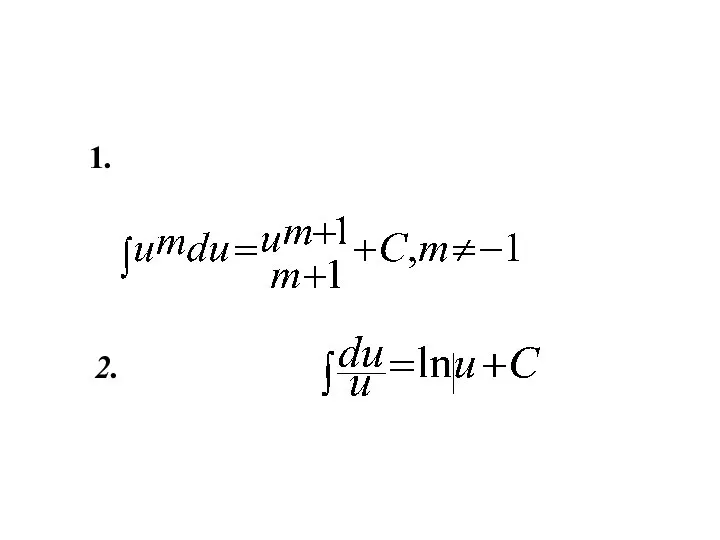
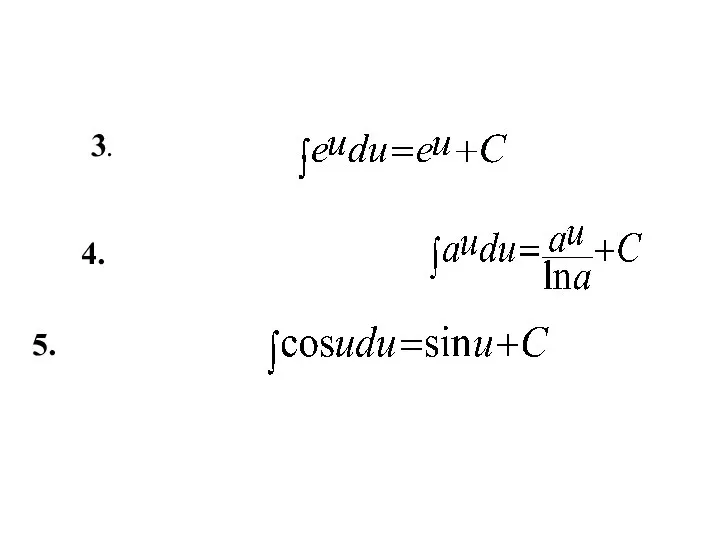
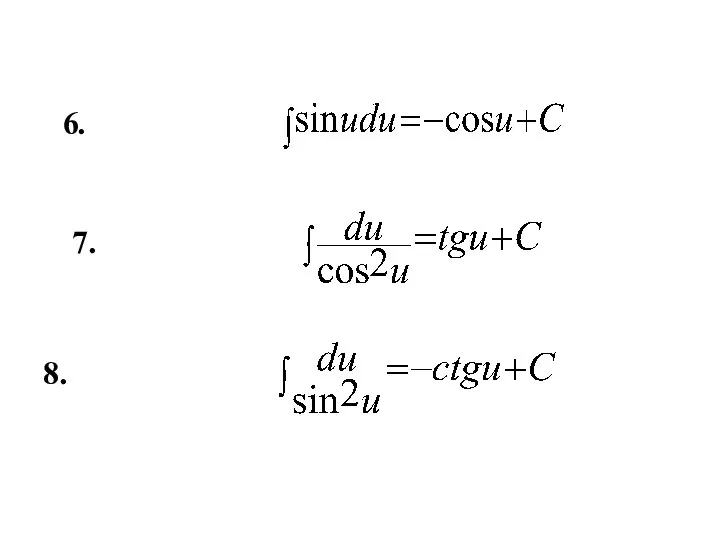
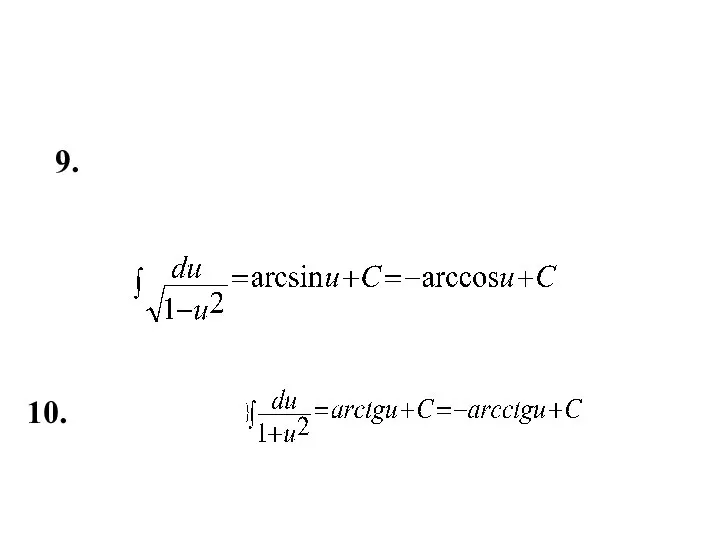




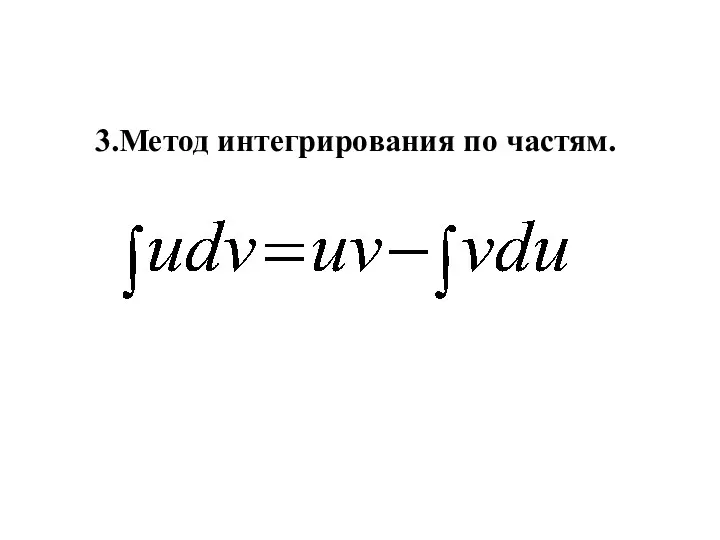

 Системи лінійних алгебраїчних рівнянь
Системи лінійних алгебраїчних рівнянь Тестовые задания для ЕНТ - 2017
Тестовые задания для ЕНТ - 2017 Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности ОГЭ по математике – 2018 год
ОГЭ по математике – 2018 год Множества. Операции над множествами
Множества. Операции над множествами Повторяем дроби
Повторяем дроби Математический бой. Внеклассное мероприятие по математике
Математический бой. Внеклассное мероприятие по математике Дифференциальные уравнения 2-го порядка Лекция 5
Дифференциальные уравнения 2-го порядка Лекция 5 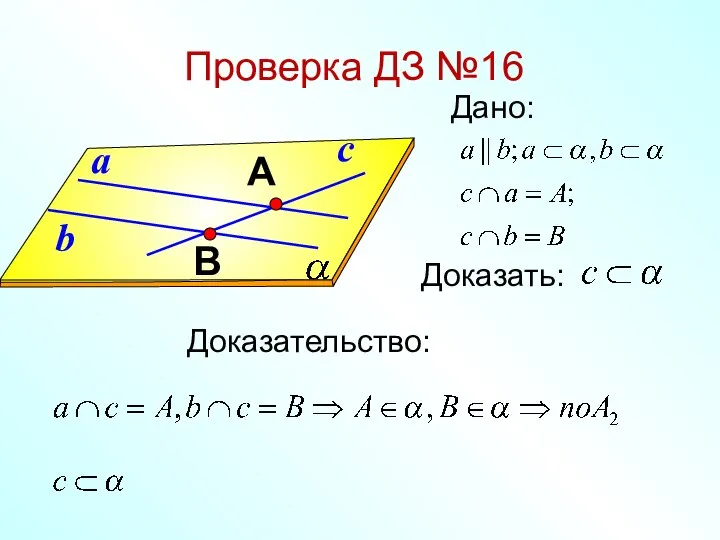 Параллельность прямой и плоскости
Параллельность прямой и плоскости Координатная плоскость
Координатная плоскость Алгебраические методы решения геометрических задач
Алгебраические методы решения геометрических задач Аксиома параллельных прямых
Аксиома параллельных прямых Пирамида. Определение, элементы, площадь поверхност и и объем пирамиды
Пирамида. Определение, элементы, площадь поверхност и и объем пирамиды Пираты Карибского моря. Математика
Пираты Карибского моря. Математика Комплексные числа
Комплексные числа Порядок выполнения действий
Порядок выполнения действий Теорема умножения вероятностей. Решение задач В-10
Теорема умножения вероятностей. Решение задач В-10 Презентация по математике "Построение прямоугольника на нелинованной бумаге" - скачать
Презентация по математике "Построение прямоугольника на нелинованной бумаге" - скачать  Геометрические тела
Геометрические тела Аттестационная работа. Создание творческого проекта «Задачи на движение»
Аттестационная работа. Создание творческого проекта «Задачи на движение» Элементы векторной алгебры (лекция № 2)
Элементы векторной алгебры (лекция № 2) Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов)
Анализ таблиц сопряжения. Меры эффекта в исследованиях (отношение рисков, шансов) Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.
Закрепление МКОУ «Петуховская средняя школа № 1» Составитель: А.А.Глухова, учитель начальных классов.  Математическая сказка «Гуси-лебеди»
Математическая сказка «Гуси-лебеди» Смежные углы
Смежные углы Алгебра и начала анализа. Логарифмическая функция Волков С.А. Урюмская средняя школа Тетюшский район Республика Татарстан
Алгебра и начала анализа. Логарифмическая функция Волков С.А. Урюмская средняя школа Тетюшский район Республика Татарстан Правильные многогранники
Правильные многогранники Методы многопарметрической оптимизации
Методы многопарметрической оптимизации