Содержание
- 2. Рассмотрим два множества X ={x1, x2 ,...,xn} и Y ={y1, y2 ,..., ym}
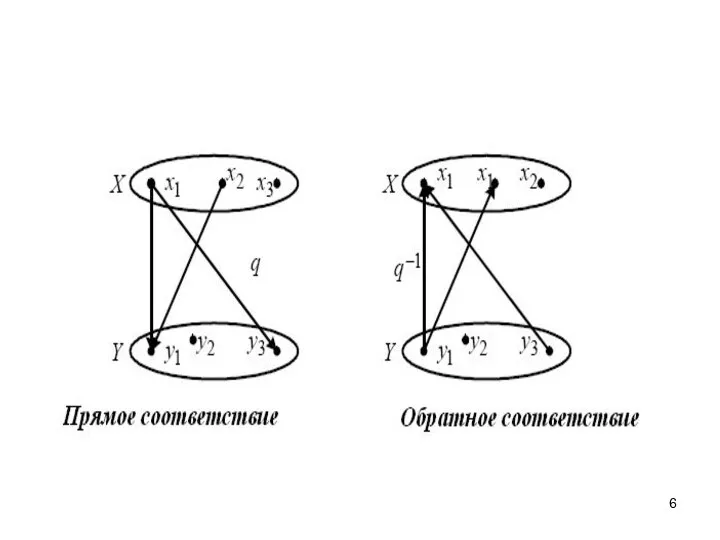
- 3. Соответствие q представляет собой тройку множеств q = (X,Y,Q), где X и Y – это множества,
- 4. Множество Q X×Y определяет закон, по которому осуществляется соответствие , т.е. перечисляет все пары, участвующие в
- 5. Для каждого q = (X, Y, Q) можно указать обратное соответствие q-1 = (X,Y,Q-1), где Q-1
- 7. Обратное соответствие обратного соответствия даст прямое соответствие (q-1)-1 = q.
- 8. Соответствие называется взаимно однозначным, если каждому элементу множества X соответствует (поставлен в пару с ним) единственный
- 9. Отображения Отображение является частным случаем соответствия (однозначное соответствие). Соответствие, характеризующее правило, по которому каждому элементу множества
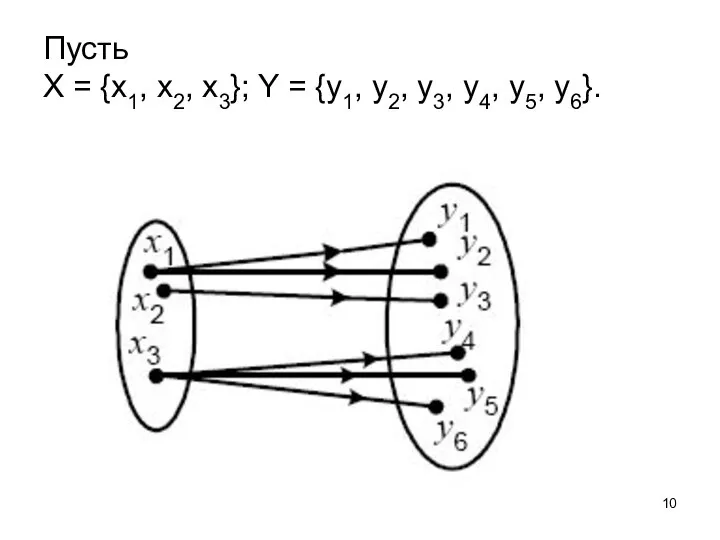
- 10. Пусть X = {х1, х2, х3}; Y = {у1, у2, у3, у4, у5, у6}.
- 11. Каждому элементу xi x отображение Г ставит в соответствие некоторое подмножество Г Y , называемое образом
- 12. Отображение называется сюръективным (или отображением "на"), если образы точек множества X заполняют все множество Y, причем
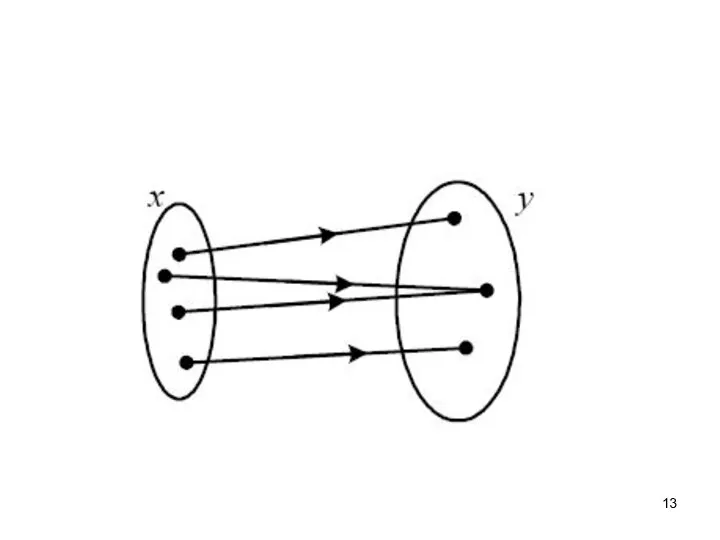
- 14. Отображение называется инъективным (или отображением "в"), если элементы множества X отображаются не на все множество Y,
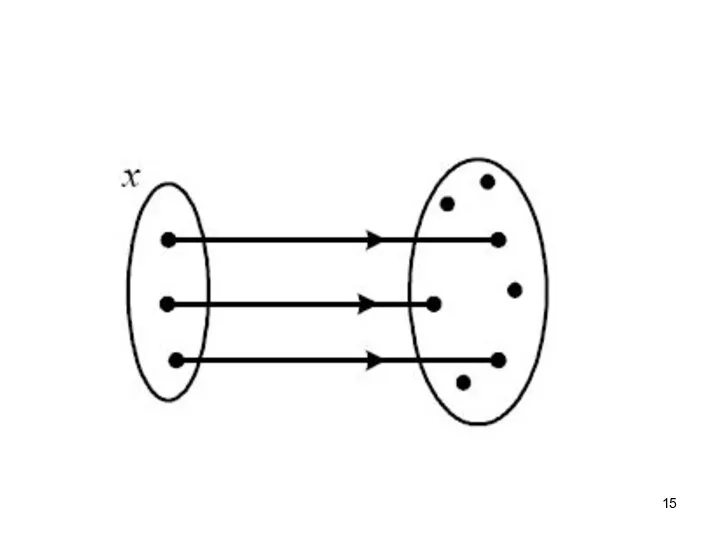
- 16. Биективное отображение является одновременно инъективным и сюръективным, т.е. является взаимно однозначным.
- 17. Важным случаем отображения является отображение элементов внутри одного множества. При этом отображение Г: Х→Х будет определяться
- 18. С помощью отображений могут быть даны определения таким понятиям, как функция, функционал, оператор.
- 19. Если отображение Г: X→Y рассматривается как соответствие между множествами X и Y, то множество f ={(x,
- 20. Таким образом, f является множеством, элементами которого являются пары (х, у), участвующие в соответствии, и f(x)
- 21. Произвольное подмножество множества А1 x А2 x…x Аn. называется отношением, заданным или определенным на множествах А1,
- 22. элементы (где ) связаны отношением R тогда и только тогда, когда , а – упорядоченный набор
- 23. Бинарным отношением (соответствием) R из A в B называется подмножество декартового произведения множеств A × B.
- 24. Если (а,b) R, это записывается как aRb; при этом говорят, что а и b находятся в
- 25. Примером отношений могут служить такие понятия: как "меньше, чем", "делится на", "включено в", "больше чем" и
- 26. Примеры отношений: а) соответствие между множеством отпечатков пальцев A = {a, b, c} и множеством подозреваемых
- 27. в) пусть А – множество товаров в магазине, а В – множество действительных чисел. Тогда {(х,у)
- 28. г) пусть А – множество женщин, а В – множество мужчин, тогда {(х,у) A × B:
- 29. е) если А = {1,2,3},а В = {r, s}, так что A × B = {(1,r),
- 30. Пример
- 31. Подмножество R декартового произведения множеств A1 A2 … An называется отношением степени n (n-арным отношением).
- 32. Если А1=А2=А3=…=Аn, то декартово произведение A1 A2 … An называется декартовым произведением n-й степени множества А(Аn),
- 33. Обобщенное понятие отношения: n-местное отношение R – множество упорядоченных наборов
- 34. Пример Отношение круг радиуса 1 с центром в начале координат, то есть множество точек плоскости, координаты
- 35. Пример Если A –конечное, то отношение задают списком пар.
- 36. Бинарное отношение можно задавать матрицей , элементы которой равны: единице, если пара принадлежит отношению R, нулю,
- 37. Пример отношения заданного матрицей
- 38. Любая матрица размерности является матрицей бинарного отношения между множествами А и В, мощность которых
- 39. Отношение между двумя элементами называется бинарным, или двухместным, между тремя-тернарным, или трехместным, между n элементами n–нарным,
- 40. Мощность множества кортежей, входящих в отношение R, называют мощностью отношения R.
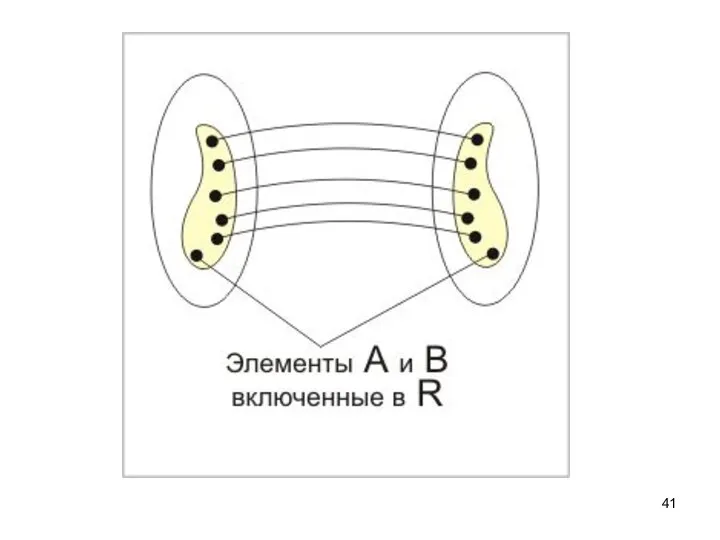
- 42. Свяжем с каждым бинарным отношением R между А и В область определения D(R) и область значений
- 43. Область определения отношения R на А и В есть множество всех х А таких, что для
- 44. Область значений отношения R на А и В есть множество всех у В таких, что для
- 45. Пример
- 47. С каждым отношением R на А В связано отношение R-1 на В А.
- 48. Пусть R А В есть отношение на А В. Тогда отношение R-1 на В А определяется
- 49. Другими словами (b,a) R-1 , тогда и только тогда, когда (а,b) R. Отношение R-1 называется обратным
- 50. Пример: R = {(x,y) | x,y N & y=x2} – отношение на множестве натуральных чисел N.
- 51. Термин «реляционное представление данных», впервые введенный Коддом, происходит от термина relation.
- 52. Во-первых, все элементы отношения есть однотипные кортежи. Например, рассмотрим отношение, состоящее из трех следующих кортежей {(1,
- 53. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой
- 54. Множество {(1), (1, 2), (1, 2, 3)}, состоит из разнотипных числовых кортежей. Это множество не является
- 55. Во-вторых. За исключением крайнего случая, когда отношение есть само декартово произведение A1 A2 … An, отношение
- 56. Для каждого отношения имеется критерий, позволяющий определить, какие кортежи входят в отношение, а какие - нет.
- 57. Каждому отношению можно поставить в соответствие некоторое логическое выражение P(x1, x2, …, xn), зависящее от n
- 58. Кортеж (a1, a2, …, an) принадлежит отношению R тогда и только тогда, когда предикат этого отношения
- 59. Каждый n-местный предикат задает некоторое n-арное отношение. Таким образом, существует взаимно однозначное соответствие между n-арными отношениями
- 60. основные свойства отношений
- 61. тождественность, рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность.
- 62. Отношение R называется тождественным на множестве A, если, оно состоит из всех пар вида (а,а), где
- 63. Отношение R называется рефлексивными на множестве А, если для всех а А справедливо аRа или (а,а)
- 64. Отношение R называется антирефлексивным, если для всех а А не выполняется аRа т.е. (а,а) R. Другими
- 65. Отношение R называется симметричным на множестве А, если для каждой пары а и b А справедливо
- 66. Отношение R называется антисимметричным на множестве А, если для каждой пары а и b А справедливо
- 67. Отношение R называется транзитивным на множестве А, если для любой тройки а,b,c А справедливо соотношение: если
- 68. Примеры: Рассмотрим следующее отношение «х делит у на множестве натуральных чисел».
- 69. Отношение рефлексивно, так как х всегда делит сам себя. Отношение не симметрично, так как 2 является
- 70. Предположим, что х делит у, а у в свою очередь делит z. Тогда из первого предположения
- 71. Отношение антисимметрично, так как если из предположения х делит у и у делит х вытекает, что
- 72. Рассмотрим следующее отношение: «количество лет х совпадает с возрастом у» на множестве всех людей».
- 73. Отношение рефлексивно, так как возраст любого человека совпадает с количеством прожитых им лет.
- 74. Отношение симметрично, так как высказывание «количество лет х совпадает с возрастом у» на множестве всех людей»
- 75. Отношение транзитивно, так как если найдутся такие три человека х, у, z, что «количество лет х
- 76. Отношение антисимметрично, так как из высказывания высказывание «количество лет х совпадает с возрастом у» и «количество
- 77. Пусть А = {1,2,3,4,5,6}, R А А R = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2),
- 78. Отношение R рефлексивно, так как для каждого а А, (а,а) R. {(1,1), (2,2), (3,3), (4,4), (5,5),
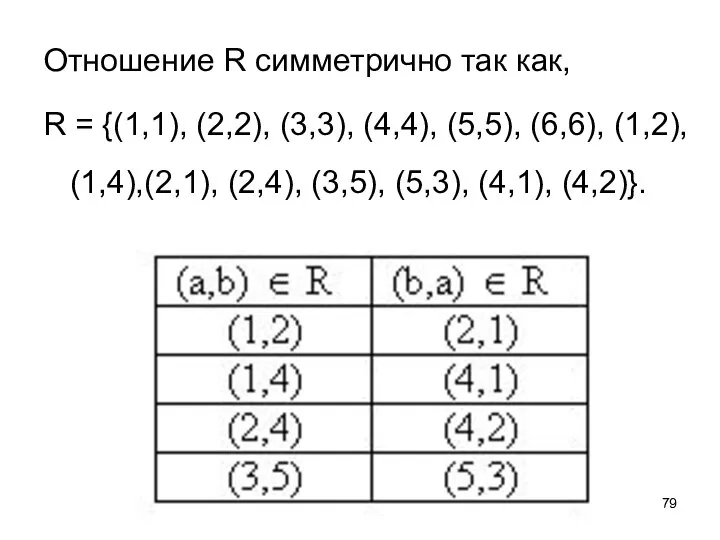
- 79. Отношение R симметрично так как, R = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2), (1,4),(2,1), (2,4),
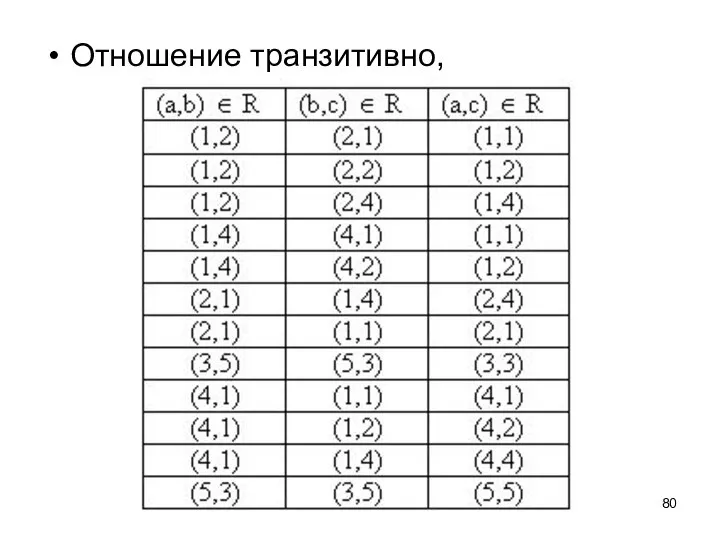
- 80. Отношение транзитивно,
- 81. Отношение R не является антисимметричным, так как, R = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6), (1,2),
- 82. Пусть А = {♠, ♣, ♥, ♦} , R А А R = {(♠,♠), (♠,♣), (♠,♦),
- 83. Отношение не рефлексивно, так как ♣ A, но (♣,♣) A , R = {(♠,♠), (♦,♦), (♥,♥)}.
- 84. Отношение не симметрично, так как R = {(♠,♠), (♠,♣), (♠,♦), (♣,♠), (♦,♠),(♦,♦), (♥,♦), (♥,♥)}
- 85. Отношение не является антисимметричным, так как R = {(♠,♠), (♠,♣), (♠,♦), (♣,♠), (♦,♠),(♦,♦), (♥,♦), (♥,♥)}
- 86. Отношение не является транзитивным, так как R = {(♠,♠), (♠,♣), (♠,♦), (♣,♠), (♦,♠),(♦,♦), (♥,♦), (♥,♥)}
- 87. Замыкание отношений
- 88. Если отношение R на множестве А не обладает тем или иным свойством, то его стоит попытаться
- 89. Под продолжением понимается присоединение некоторых упорядоченных пар к подмножеству
- 90. Новое полученное множество R* уже будет обладать требуемым свойством. Исходное множество R будет подмножеством R*.
- 91. Если вновь построенное множество R* будет минимальным среди всех расширений R с выделенным свойством, то R*
- 92. Рефлексивное замыкание R есть наименьшее рефлексивное отношение на A, содержащее R как подмножество.
- 93. Рефлексивным замыканием Ri отношения R называется отношение , где i – отношение тождества на А (диагональ).
- 94. Симметричное замыкание R наименьшее симметричное отношение на A, содержащее R как подмножество.
- 95. Симметричным замыканием Rs отношения R называется отношение т.е. если (а,b) R, то (а,b) Rs и (b,a)
- 96. Транзитивное замыкание R наименьшее транзитивное отношение на A, содержащее R как подмножество.
- 97. Транзитивным замыканием Rt отношения R называется отношение т.е. (а,b) Rt тогда и только тогда, когда существуют
- 98. Пример А = {1,2,3}, отношение R на А задано упорядоченными парами R = {(1,1), (1,2), (1,3),
- 99. Замыкание относительно рефлексивности должно содержать все пары вида (а,а). Поэтому, искомое замыкание имеет вид: Добавленные пары
- 100. Замыкание относительно симметричности должно содержать все пары, симметричные исходным.
- 101. Замыкание относительно транзитивности. Необходимо выполнить несколько шагов. Отношение R = {(1,1), (1,2), (1,3), (3,1),(2.3)}: содержит пары
- 103. Появились пары (2,1) и (1,2). Следовательно, замыкание R* должно содержать пару (2,2). Все необходимые пары перебрали.
- 105. Пусть А = {а1, а2, а3,а4}, R = {(а1,а3), (а3,а4), (а4,а2), (а3,а3)}.
- 106. Ri = {(а1,а3), (а3,а4), (а4,а2), (а3,а3); (а1,а1), (а2,а2), (а4,а4)}.
- 107. Rs = {(а1,а3), (а3,а1), (а3,а4), (а4,а3); (а4,а2), (а2,а4), (а3,а3)}.
- 109. Скачать презентацию







































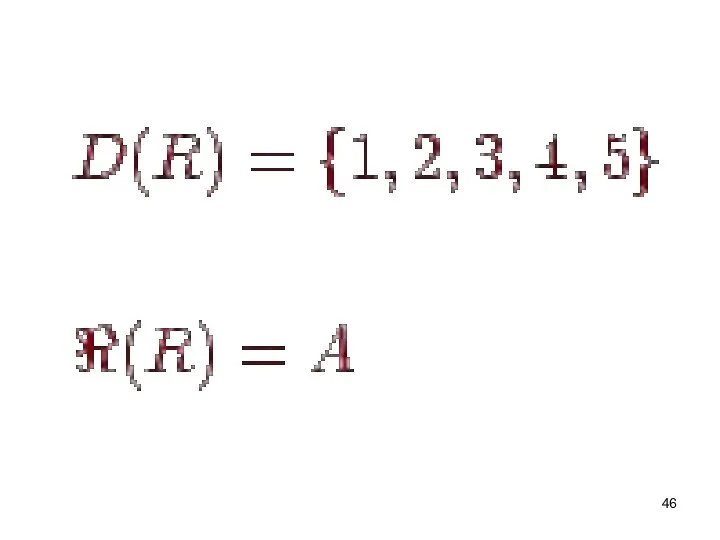

































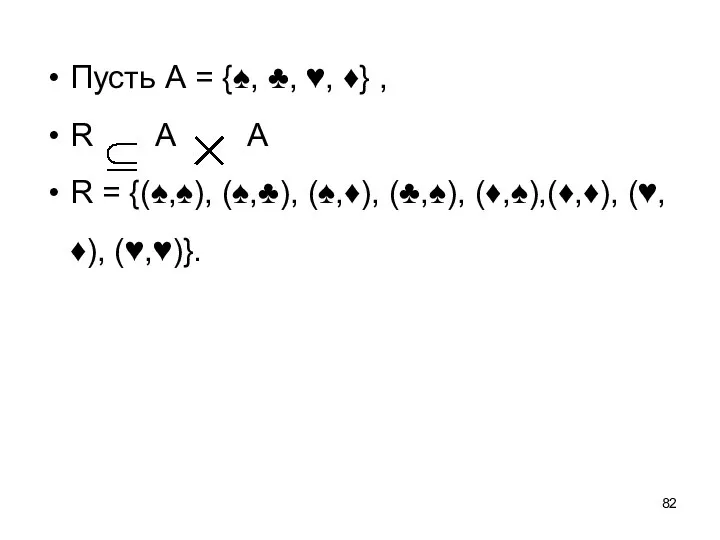






















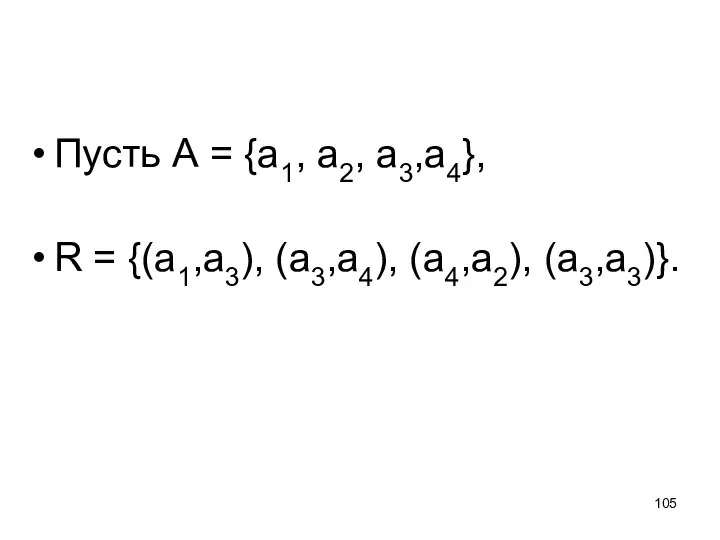

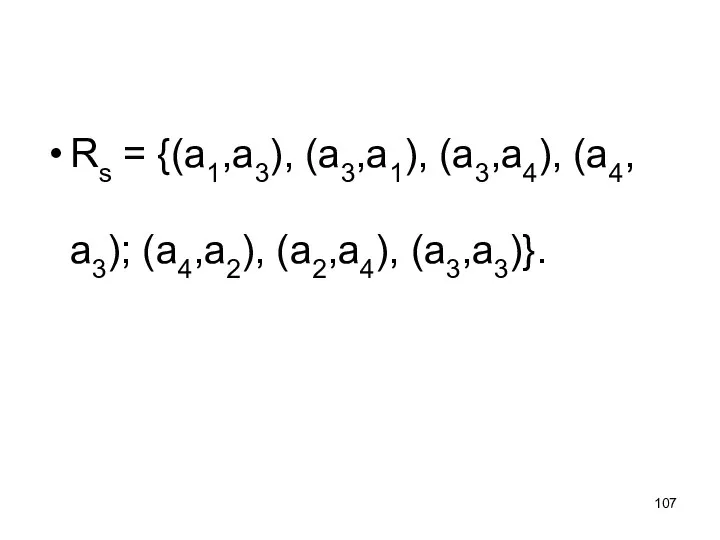
 Трапеция 1
Трапеция 1 Формулы приведения. Формулы для вычисления координат точек
Формулы приведения. Формулы для вычисления координат точек Основная информация по геометрии
Основная информация по геометрии Алгоритмы решения систем линейных алгебраических уравнений
Алгоритмы решения систем линейных алгебраических уравнений Декартова система координат в пространстве и на плоскости. Полярная система координат на плоскости
Декартова система координат в пространстве и на плоскости. Полярная система координат на плоскости Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Математическое развитие детей в семье
Математическое развитие детей в семье Сведение двойного интеграла к повторному
Сведение двойного интеграла к повторному Решение задач по теории вероятностей
Решение задач по теории вероятностей Геометрия. Виды треугольников
Геометрия. Виды треугольников Угол
Угол Решение систем уравнений
Решение систем уравнений Понятие симметрии
Понятие симметрии Перпендикуляр к прямой. Медианы, биссектрисы, высоты треугольника
Перпендикуляр к прямой. Медианы, биссектрисы, высоты треугольника Корреляционно-регрессионный анализ
Корреляционно-регрессионный анализ “Математика озаты” интеллектуалдық олимпиада
“Математика озаты” интеллектуалдық олимпиада Вычитание векторов. Умножение вектора на число
Вычитание векторов. Умножение вектора на число Числовые выражения, содержащие знаки + и -
Числовые выражения, содержащие знаки + и - Применение производной к исследованию функции
Применение производной к исследованию функции Пряма та обернена теорема Вієта та їх застосування
Пряма та обернена теорема Вієта та їх застосування Тест по теме: "Прямоугольный параллелепипед". Часть 2. Вариант 2
Тест по теме: "Прямоугольный параллелепипед". Часть 2. Вариант 2 Научные фокусы и загадки
Научные фокусы и загадки Тема проекта: Максимум удовольствия, оптимизация затрат
Тема проекта: Максимум удовольствия, оптимизация затрат Случайные величины
Случайные величины Смешанные числа
Смешанные числа Цилиндр. Задачи
Цилиндр. Задачи Метод логических рассуждений
Метод логических рассуждений Правильные многоугольники
Правильные многоугольники