Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции
Содержание
- 2. 1. Предел в точке. Рассмотрим пример. Построить график функции
- 3. 1 2
- 4. В этом случае пишут: По-другому: при
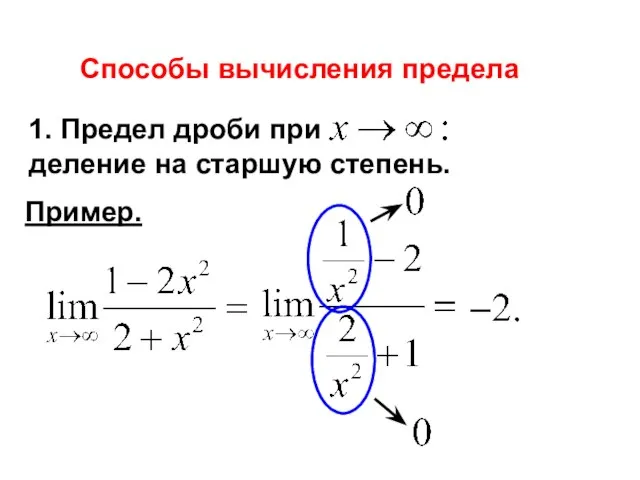
- 5. Способы вычисления предела 1. Предел дроби при деление на старшую степень. Пример.
- 6. 2. Разложение на множители, когда Пример.
- 7. Односторонние пределы Пример 1.
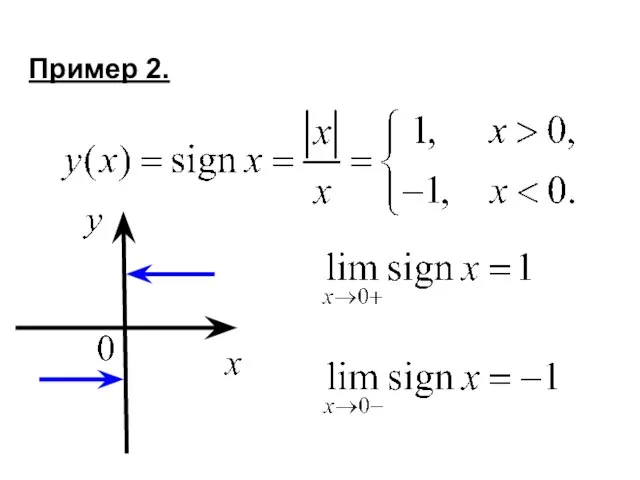
- 8. Пример 2.
- 9. Опр. Функция называется непрерывной в точке если Все элементарные функции непрерывны на своей области определения. Пример.
- 10. Опр. Если в точке функция не является непрерывной, то - точка разрыва. Рассматриваются точки разрыва 1-го
- 11. Пример. - точка разрыва 1-го рода (конечный разрыв).
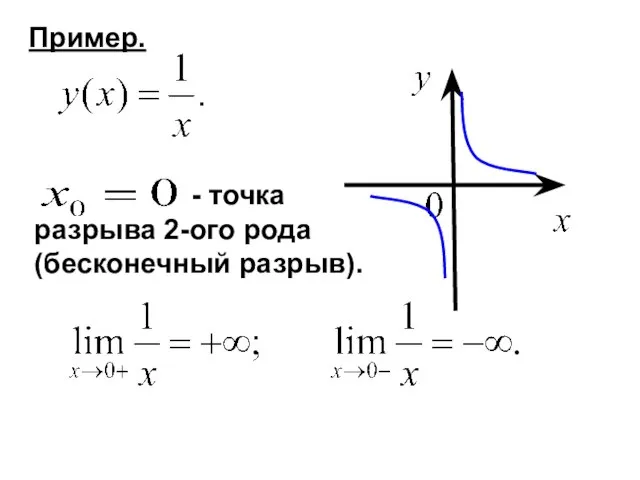
- 12. Пример. - точка разрыва 2-ого рода (бесконечный разрыв).
- 13. Тема: Производная функции, правила вычисления. Производная сложной функции. Производные высших порядков. Дифференциал функции.
- 14. Приращение аргумента и приращение функции Пусть дана функция Рассмотрим два значения её аргумента: исходное и новое
- 15. называется приращением функции и обозначается Опр. Производной функции в точке называется
- 16. Пример. Найти производную функции Найдем Таким образом
- 17. Эта производная определена на всей числовой оси, так как при её нахождении значение было выбрано произвольно.
- 18. Геометрический смысл производной Угловой коэффициент касательной к графику функции в точке с абсциссой равен значению производной
- 19. Функция не имеет производной в точке т.к. график функции в точке не имеет касательной.
- 20. Таблица производных (степени)
- 21. Таблица производных (тригонометрия)
- 22. Таблица производных (arc-тригонометрия)
- 23. Основные правила дифференцирования Если функции и дифференцируемы в данной точке то в этой точке дифференцируемы и
- 24. Если функции и дифференцируемы в данной точке и то в той же точке дифференцируемо и их
- 25. 1) Найти Примеры.
- 26. 2) Найти
- 27. Производная сложной функции Пусть и Тогда есть сложная функция Теорема
- 28. Примеры 1) 2) Запишем
- 29. Производные высших порядков Пусть функция дифференцируема в некотором интервале. Тогда её производная является функцией от Пусть
- 30. Аналогично, и т.д.: Производные порядка выше первого называются производными высшего порядка.
- 31. 1) Найти производную третьего порядка от функции Примеры. 2) Найти
- 32. Рассмотрим функцию Найдем Дифференциал функции
- 33. Приращение функции можно рассматривать как сумму двух слагаемых: - линейное относительно - нелинейное относительно
- 34. При оба слагаемых стремятся к нулю, но второе слагаемое быстрее стремится к нулю. Поэтому при малых
- 35. Теорема. Если функция имеет в точке дифференциал, то она имеет в этой точке производную и наоборот,
- 36. Примеры. Найти дифференциалы функций 1) 2)
- 37. Теорема. Если функция дифференцируема в точке то она в этой точке непрерывна. Связь между дифференцируемостью и
- 38. Пример. В точке функция непрерывна, так как
- 39. Справа от нуля поэтому Слева от нуля поэтому
- 41. Скачать презентацию


































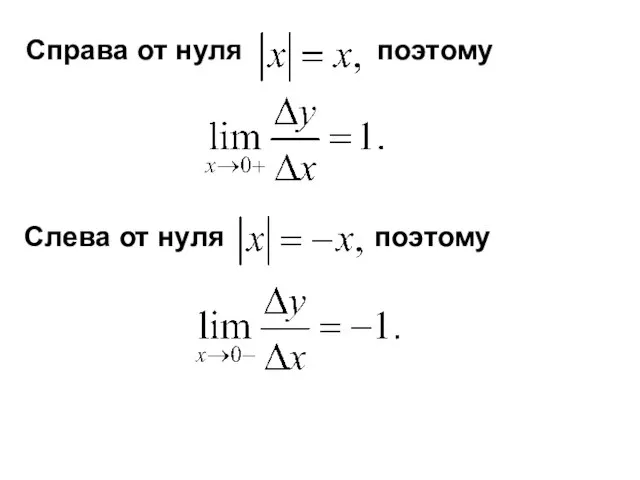
 Задание №15 базового уровня. Равнобедренный треугольник: вычисление элементов
Задание №15 базового уровня. Равнобедренный треугольник: вычисление элементов Звездный час. 5 класс
Звездный час. 5 класс Нахождение числа по его дроби
Нахождение числа по его дроби Проверка статистических гипотез
Проверка статистических гипотез Дробные выражения
Дробные выражения Основы прикладной теории упругости
Основы прикладной теории упругости Третий признак равенства треугольников
Третий признак равенства треугольников Умножение и деление. Простые задачи
Умножение и деление. Простые задачи УРОК МАТЕМАТИКИ 6 КЛАСС «Нахождение числа по его дроби»
УРОК МАТЕМАТИКИ 6 КЛАСС «Нахождение числа по его дроби»  Четырехугольники. Проверочная работа по чертежам
Четырехугольники. Проверочная работа по чертежам Математика вокруг нас. Викторина
Математика вокруг нас. Викторина Взаимные положения прямой и плоскости, двух плоскостей
Взаимные положения прямой и плоскости, двух плоскостей Set Theory
Set Theory Решение уравнений
Решение уравнений Математика. Задания на лето. Часть 3
Математика. Задания на лето. Часть 3 Практическая работа. Одночлен
Практическая работа. Одночлен Сложение и вычитание в пределах 10
Сложение и вычитание в пределах 10 Смешанные дроби
Смешанные дроби Отношения и пропорции
Отношения и пропорции Треугольники и их виды
Треугольники и их виды Переводы чисел из одной системы счисления в другую
Переводы чисел из одной системы счисления в другую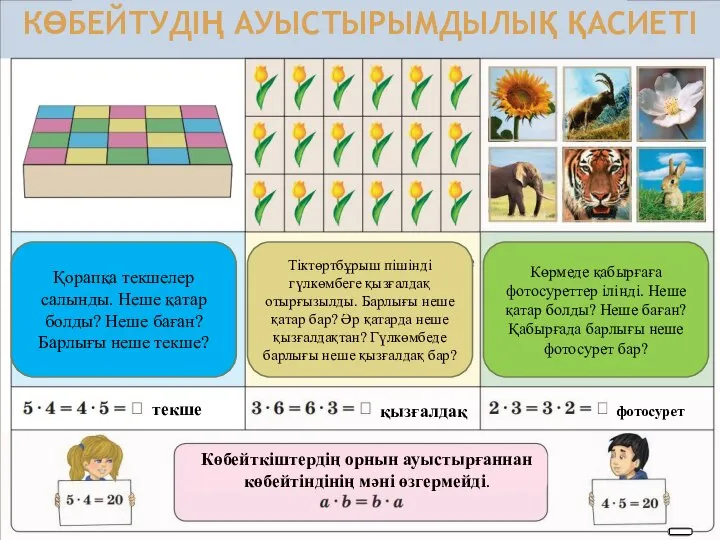 Көбейтудің ауыстырымдылық қасиеті
Көбейтудің ауыстырымдылық қасиеті Сложение и вычитание дробей
Сложение и вычитание дробей Трикутники. Види трикутників. Казка (математика 5 клас)
Трикутники. Види трикутників. Казка (математика 5 клас) В мире необыкновенных животных
В мире необыкновенных животных Логарифмы вокруг нас
Логарифмы вокруг нас Решение уравнений. 6 класс
Решение уравнений. 6 класс Электронное приложение к уроку по геометрии в 8 классе «Теорема Пифагора». Методическая разработка
Электронное приложение к уроку по геометрии в 8 классе «Теорема Пифагора». Методическая разработка