Преобразование графиков функции с помощью элементарных преобразований

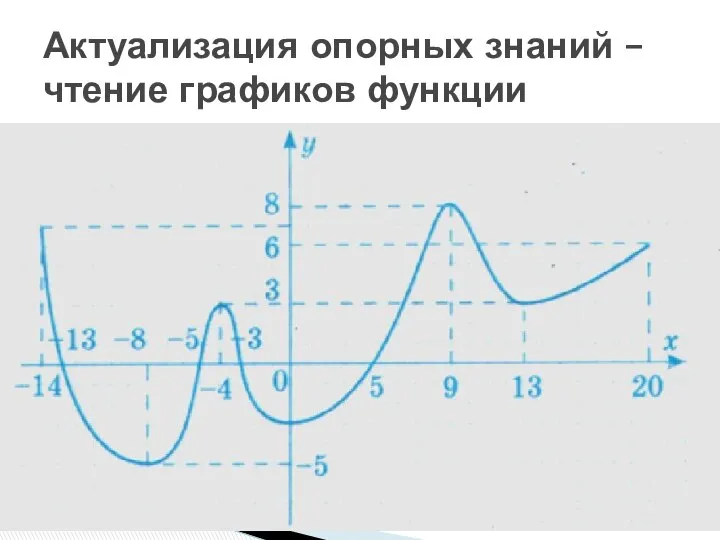
Актуализация опорных знаний – чтение графиков функции

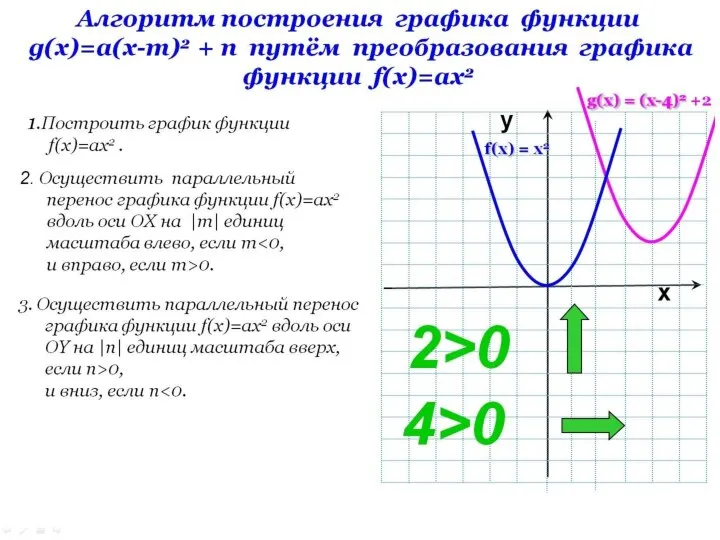
1) Систематизировать приемы построения графиков.
2) Показать их применение при построении графиков сложных функций;

Цели:

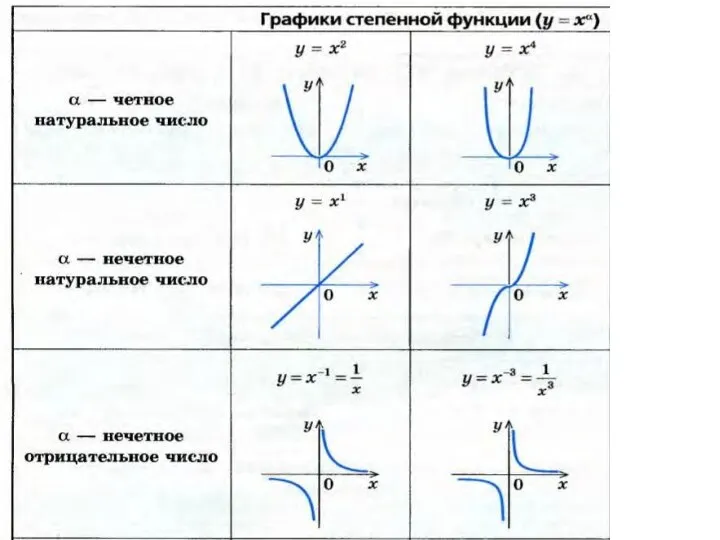
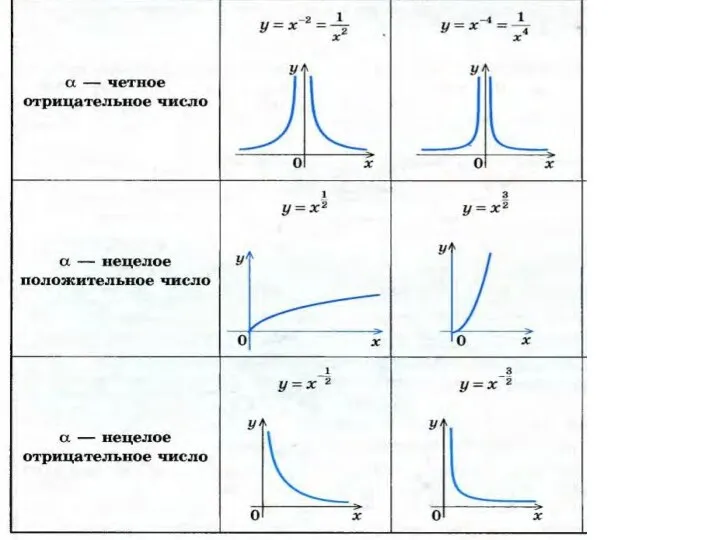
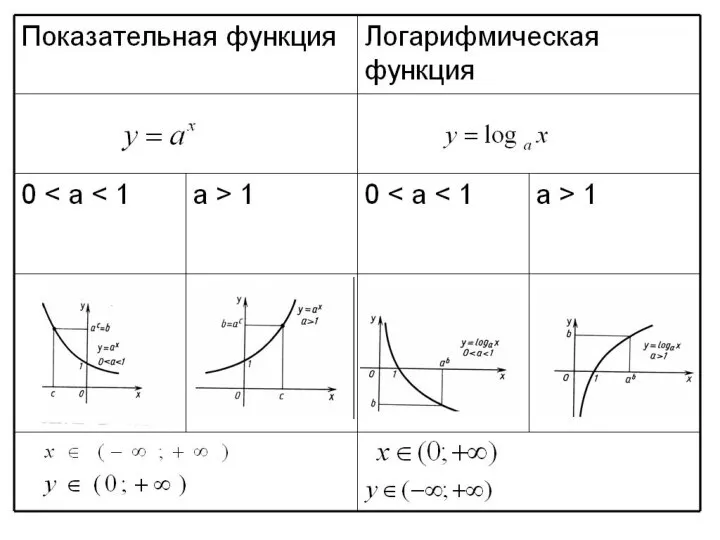
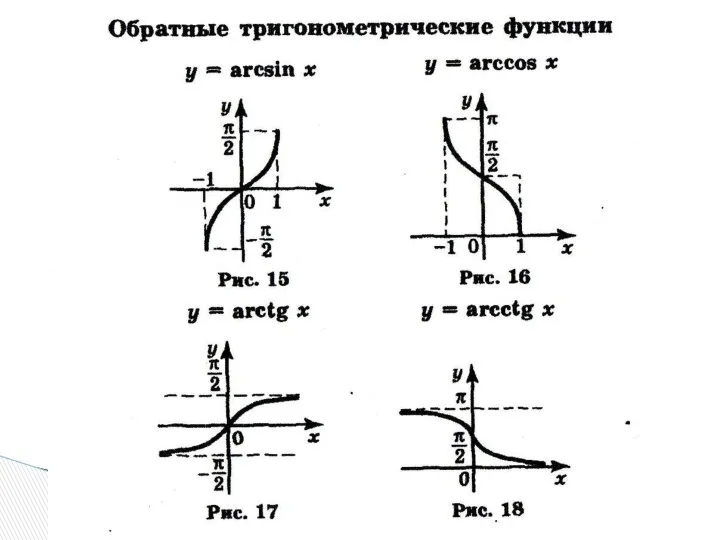
Рассмотрим основные правила преобразования графиков на примерах элементарных функций

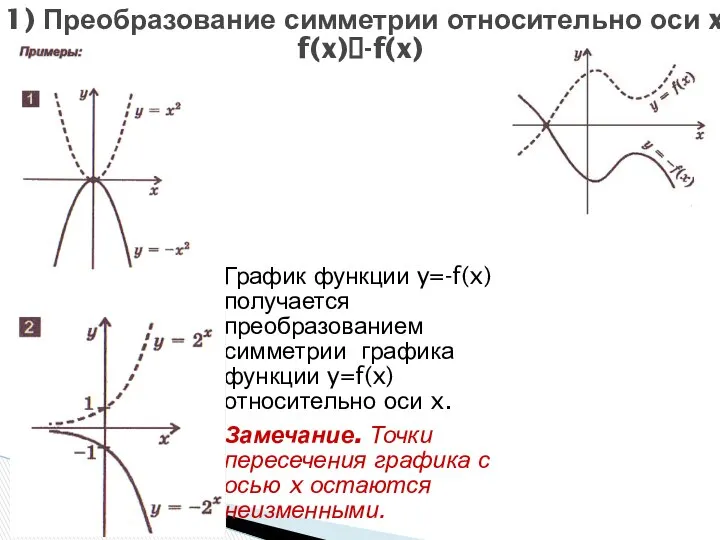
1) Преобразование симметрии относительно оси x f(x)?-f(x)

График функции y=-f(x) получается преобразованием симметрии

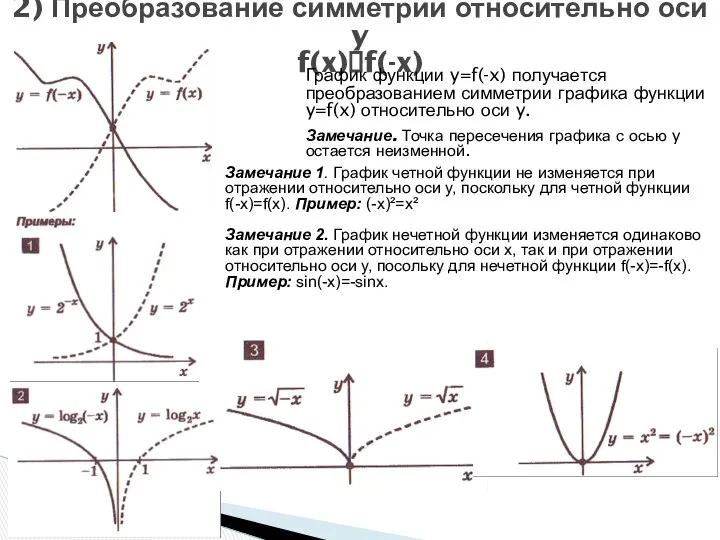
2) Преобразование симметрии относительно оси y f(x)?f(-x)

График функции y=f(-x) получается преобразованием симметрии

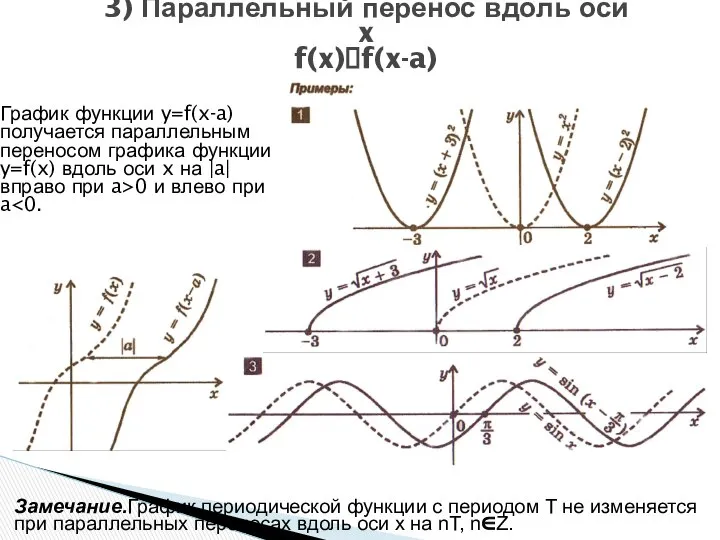
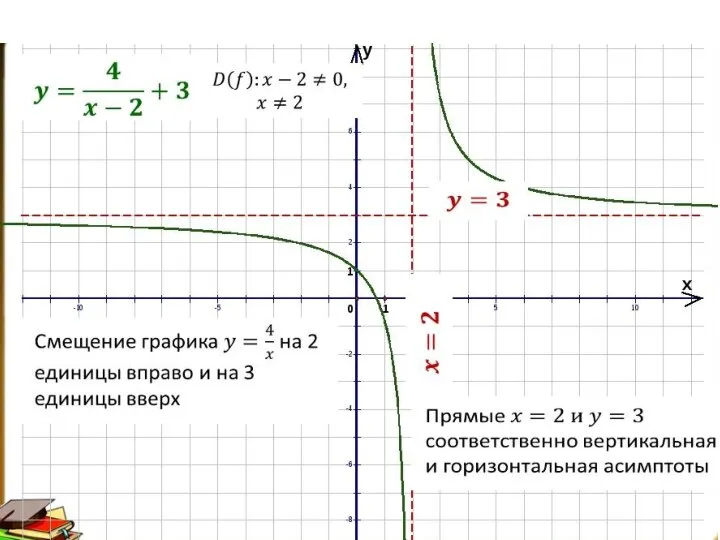
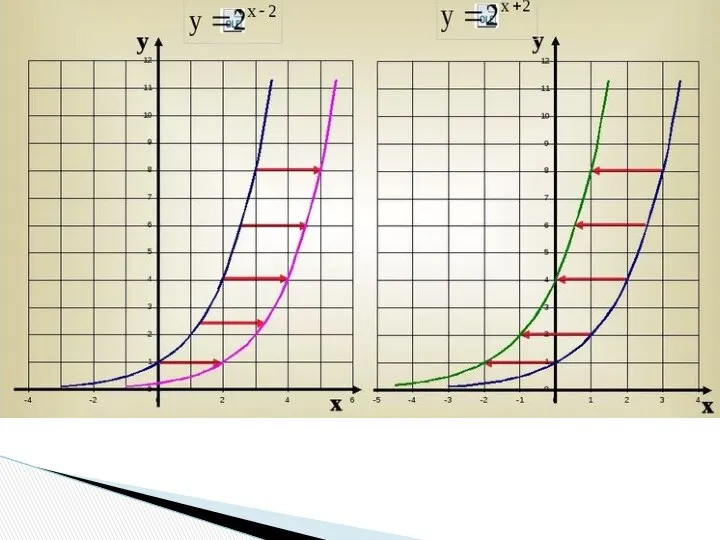
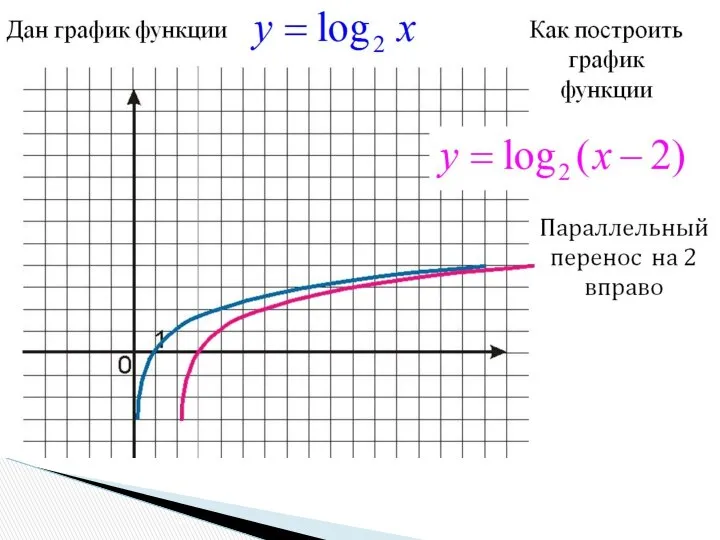
3) Параллельный перенос вдоль оси x f(x)?f(x-a)

График функции y=f(x-a) получается параллельным

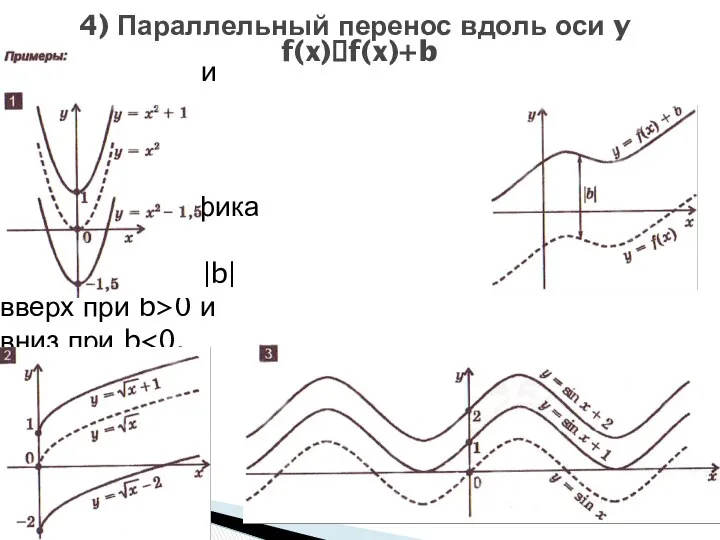
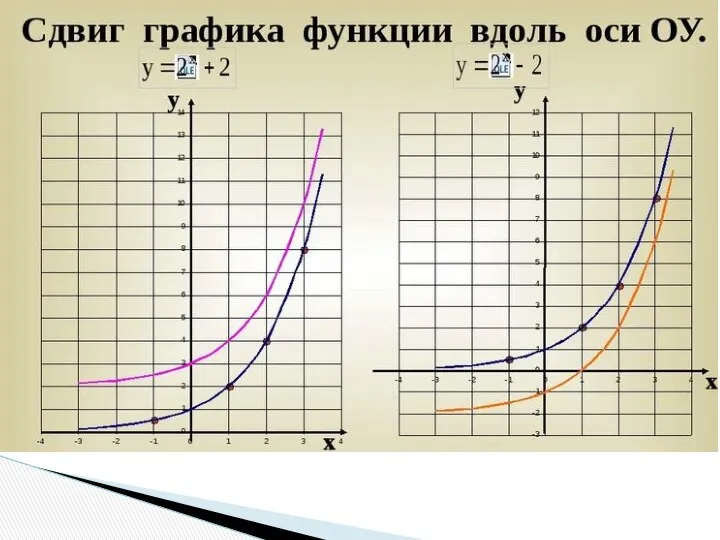
4) Параллельный перенос вдоль оси y f(x)?f(x)+b

График функции y=f(x)+b получается параллельным

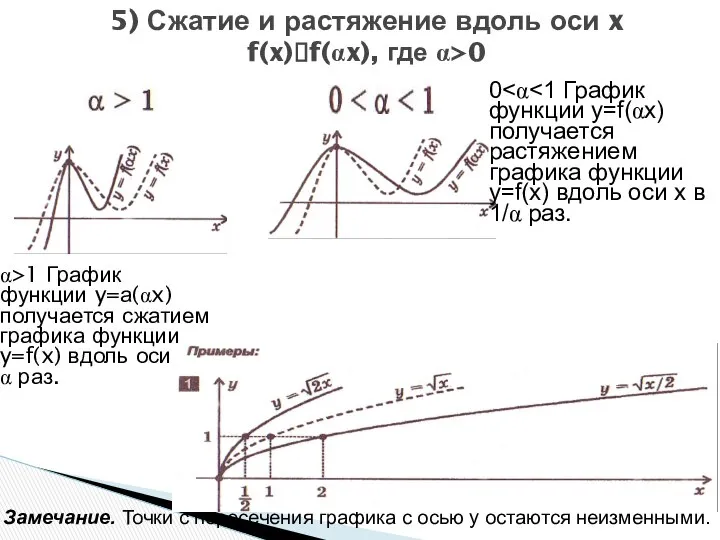
5) Сжатие и растяжение вдоль оси x f(x)?f(αx), где α>0

α>1 График функции

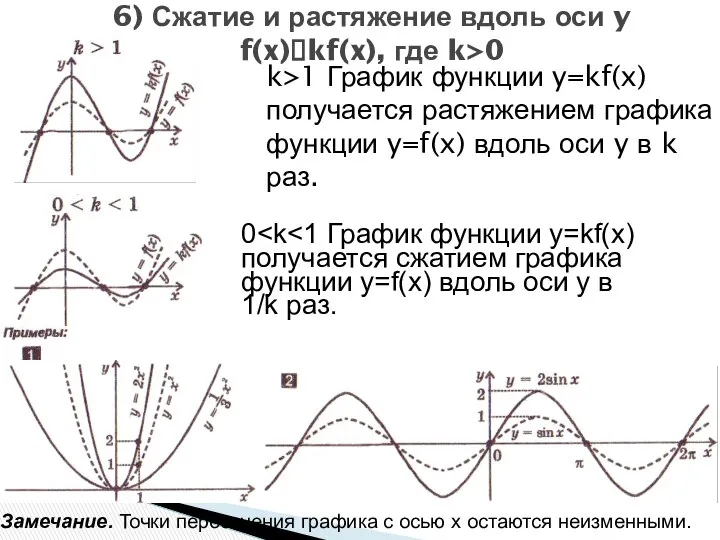
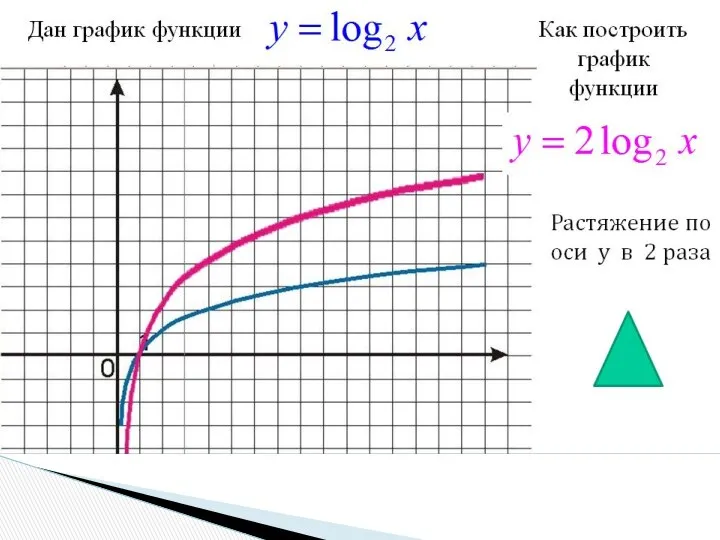
6) Сжатие и растяжение вдоль оси y f(x)?kf(x), где k>0

k>1 График функции

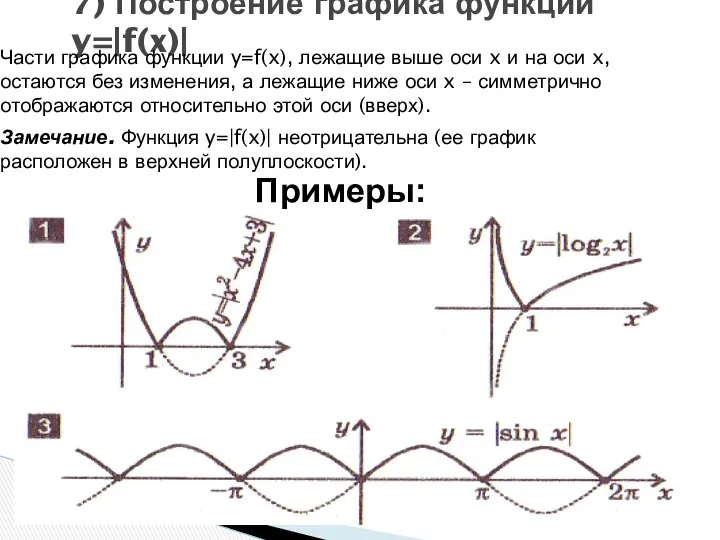
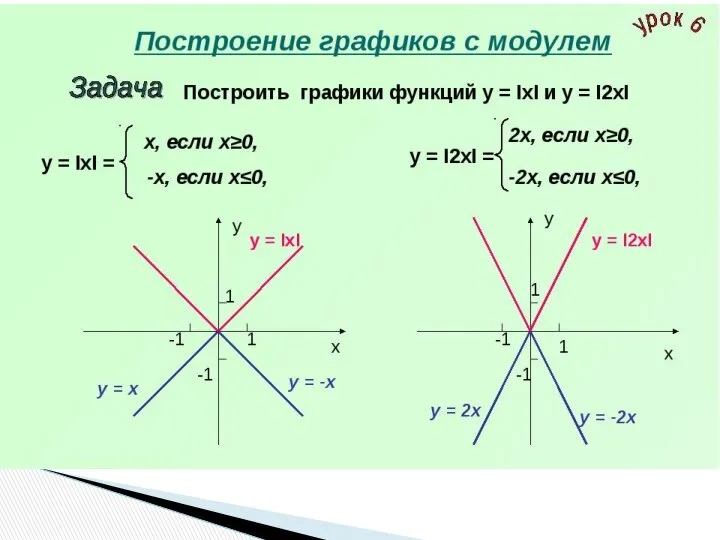
7) Построение графика функции y=|f(x)|

Части графика функции y=f(x), лежащие выше оси

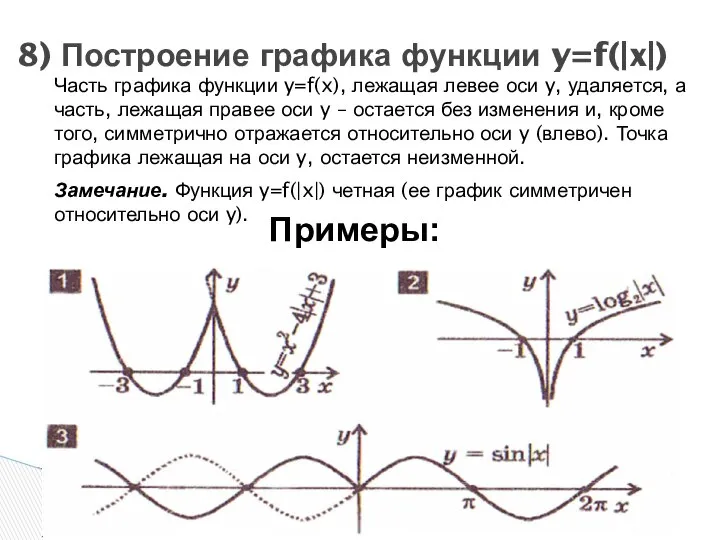
8) Построение графика функции y=f(|x|)

Часть графика функции y=f(x), лежащая левее оси

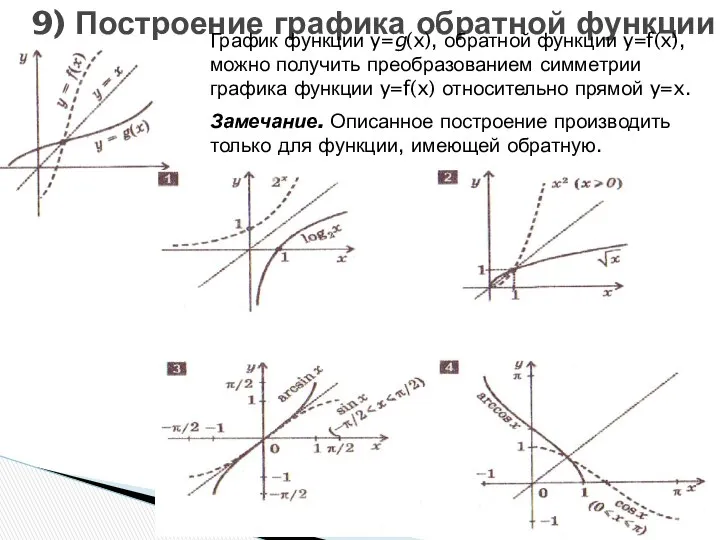
9) Построение графика обратной функции

График функции y=g(x), обратной функции y=f(x), можно

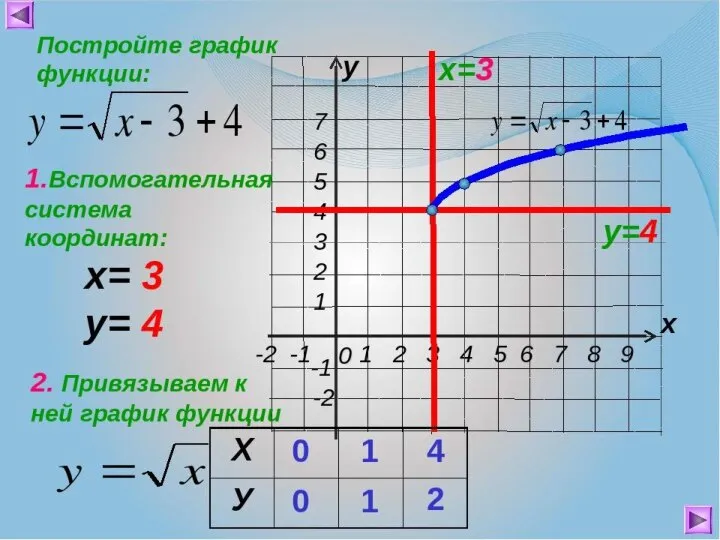
Построение графиков сложных функций с помощью последовательных преобразований графиков элементарных функций

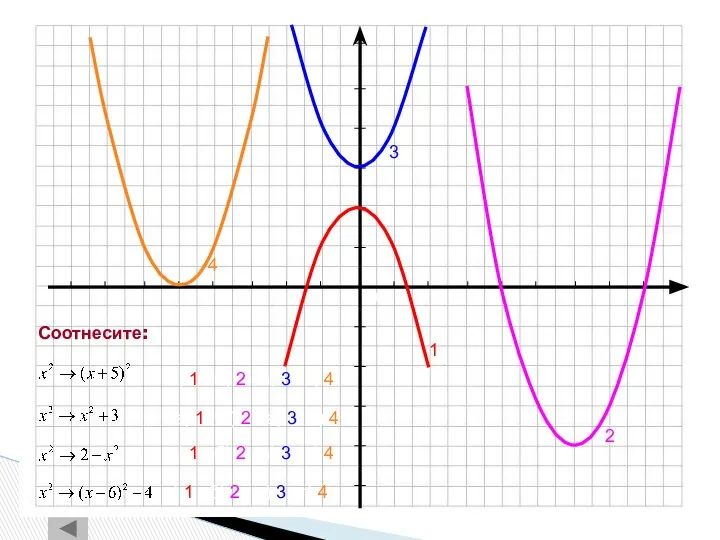
4

1

2

3

а) 1 б) 2 в) 3 г) 4

а) 1 б) 2

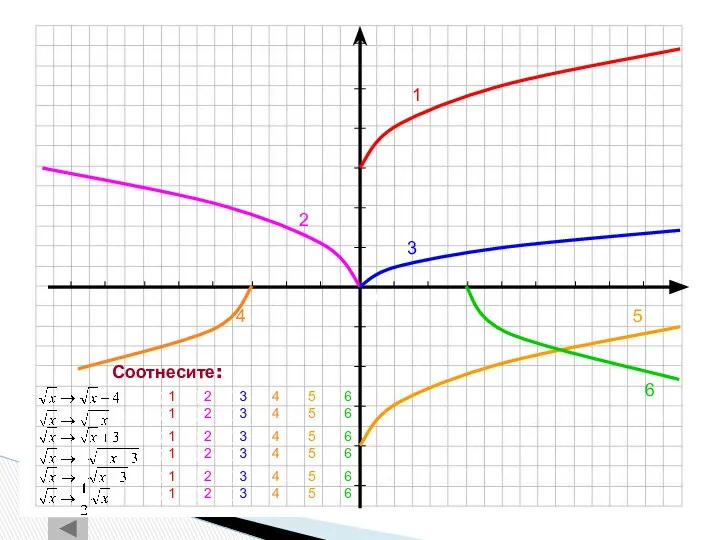
а) 1 б) 2 в) 3 г) 4 д) 5 е)

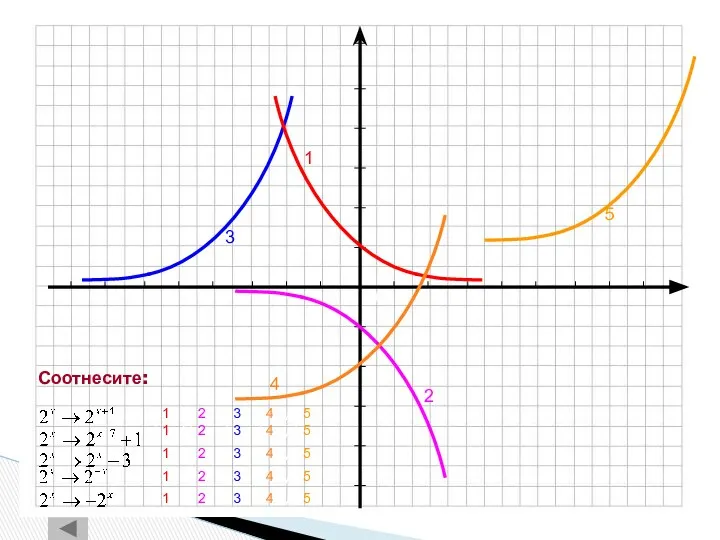
4

1

2

3

5

а) 1 б) 2 в) 3 г) 4 д) 5

а) 1