Приближенное решение алгебраических и трансцендентных уравнений. Решение уравнений с одной переменной. Лекция 5
Содержание
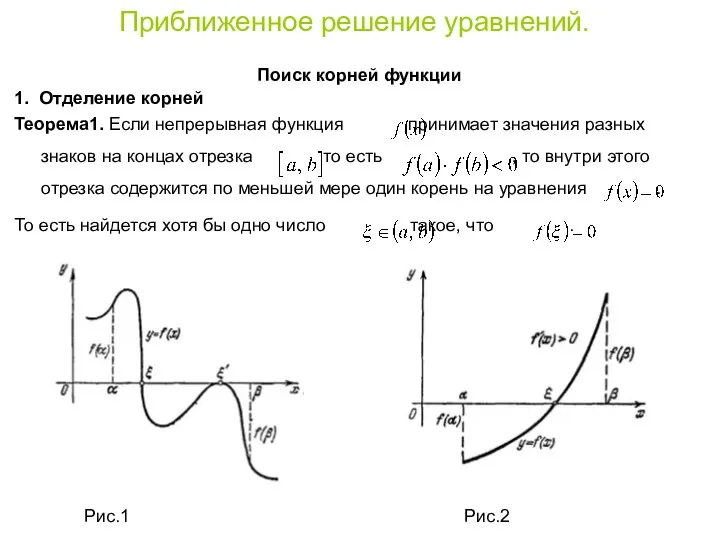
- 2. Приближенное решение уравнений. Поиск корней функции 1. Отделение корней Теорема1. Если непрерывная функция принимает значения разных
- 3. Приближенное решение уравнений. Поиск корней функции 2. Получение приближенного значения корня. Оценка погрешности // доказательство на
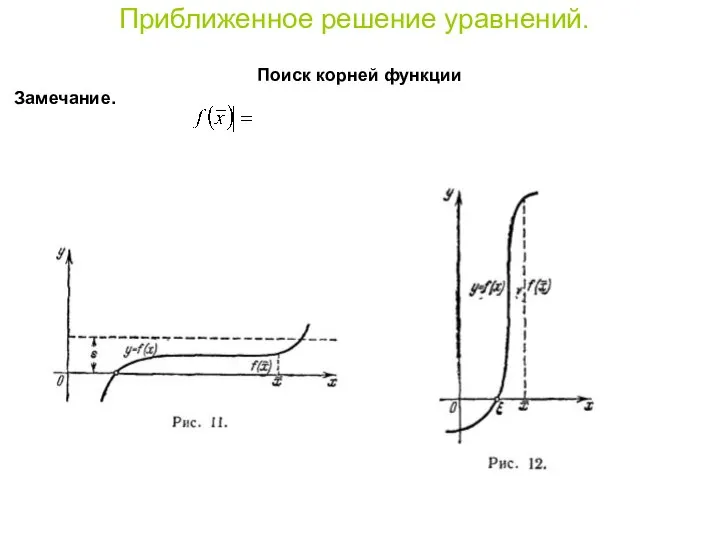
- 4. Приближенное решение уравнений. Поиск корней функции Замечание.
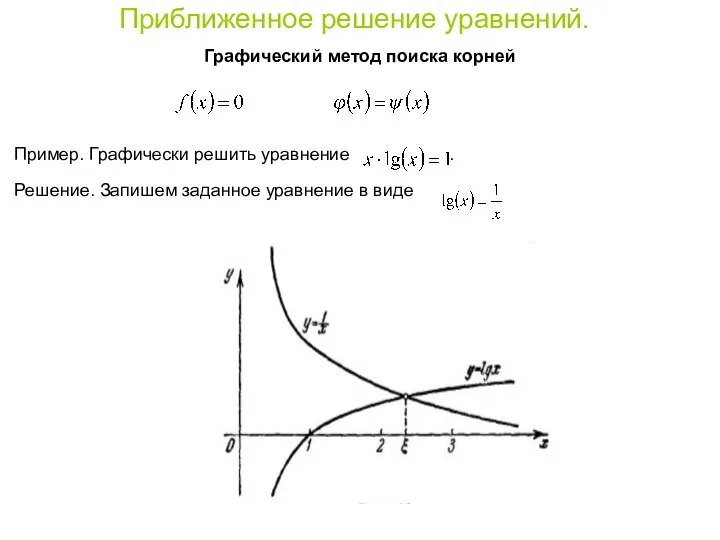
- 5. Приближенное решение уравнений. Графический метод поиска корней Пример. Графически решить уравнение . Решение. Запишем заданное уравнение
- 6. Приближенное решение уравнений. Метод дихотомии (половинного деления) Функция непрерывна на отрезке [a,b] и имеет единственный корень
- 7. Приближенное решение уравнений. Метод дихотомии (половинного деления) - монотонно неубывающая ограниченная последовательность. Следовательно, существует такое, что
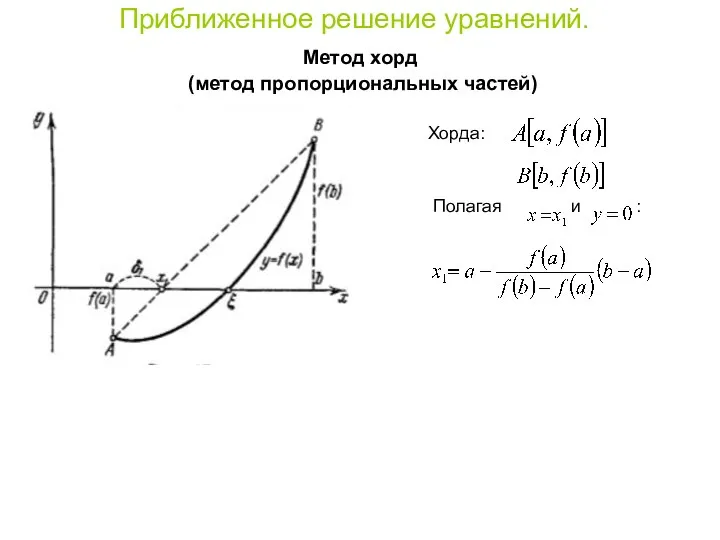
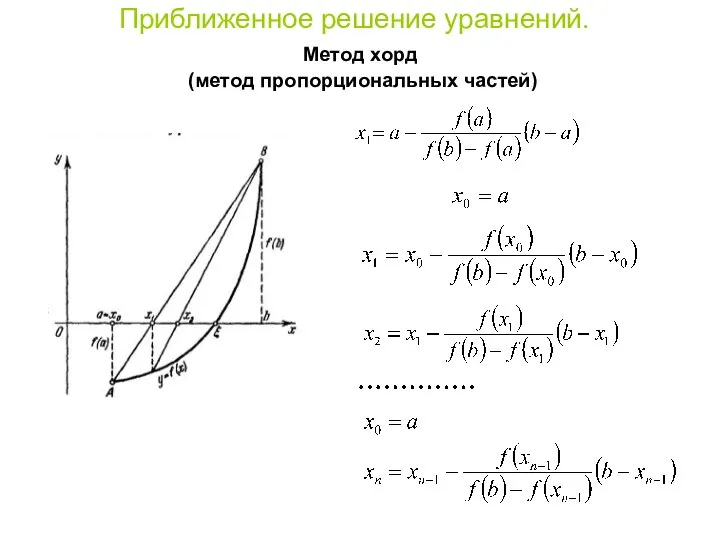
- 8. Приближенное решение уравнений. Метод хорд (метод пропорциональных частей) Хорда: Полагая и :
- 9. Приближенное решение уравнений. Метод хорд (метод пропорциональных частей)
- 10. Приближенное решение уравнений. Метод хорд (метод пропорциональных частей) (3) Последовательность ограничена и монотонна, следовательно:
- 12. Скачать презентацию




 Презентация по математике "Моделирование составных задач" - скачать
Презентация по математике "Моделирование составных задач" - скачать  Логарифмические и показательные уравнения. Математический КВН
Логарифмические и показательные уравнения. Математический КВН Умножение дробей
Умножение дробей Зависимость расположения параболы от её коэффициента
Зависимость расположения параболы от её коэффициента МУ ЗАТО Северск СОШ №84
МУ ЗАТО Северск СОШ №84 Техника дифференцирования и интегрирования
Техника дифференцирования и интегрирования Доли. Обыкновенные дроби
Доли. Обыкновенные дроби  Образцы оформления задач 1 класс
Образцы оформления задач 1 класс Презентация на тему Сумма углов треугольника
Презентация на тему Сумма углов треугольника 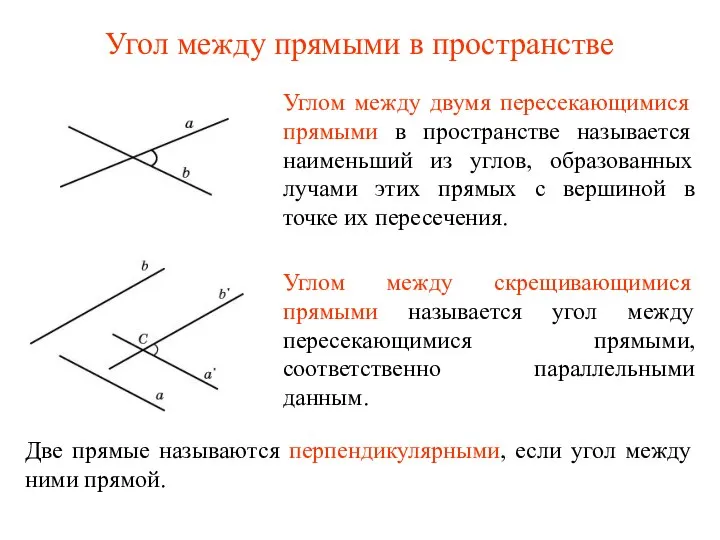 Угол между прямыми в пространстве
Угол между прямыми в пространстве Функции и графики. Чтение графиков, простейшие свойства функций
Функции и графики. Чтение графиков, простейшие свойства функций Смежные и вертикальные углы
Смежные и вертикальные углы Множество. Число элементов множества. Подмножество
Множество. Число элементов множества. Подмножество Система MatLab/ Методические указания к выполнению лабораторных работ
Система MatLab/ Методические указания к выполнению лабораторных работ Решение тригонометрических уравнений
Решение тригонометрических уравнений Перпендикуляр и наклонные. Расстояние от точки до плоскости
Перпендикуляр и наклонные. Расстояние от точки до плоскости Геометрия. Треугольники
Геометрия. Треугольники компоненты деления с остатком
компоненты деления с остатком Основы статистики. Магия цифр: когда стоит сомневаться в статистике?
Основы статистики. Магия цифр: когда стоит сомневаться в статистике? Функциональное зонирование
Функциональное зонирование Симметрия вокруг нас
Симметрия вокруг нас Простейшие задачи в координатах
Простейшие задачи в координатах Линейное уравнение с одной переменной
Линейное уравнение с одной переменной Уменьшаемое. Вычитаемое. Разность
Уменьшаемое. Вычитаемое. Разность Логарифмы вокруг нас
Логарифмы вокруг нас Векторы. Задания
Векторы. Задания Ведение в вейлет преобразование
Ведение в вейлет преобразование Математическое моделирование (дополнительные главы математики)
Математическое моделирование (дополнительные главы математики)