Содержание
- 2. Каждого изучающего математику интересует как и где применяются полученные знания
- 3. создание дидактических материалов для учителей математики, внедрение которых в учебный процесс в ходе изучения тригонометрии позволит
- 4. Содержание. Графические представления о превращении "мало интересных" тригонометрических функций в оригинальные кривые Страницы истории Прикладная направленность
- 5. Слово «тригонометрия» впервые встречается в 1505 году в заглавии книги немецкого теолога и математика Питискуса. Происхождение
- 6. Тригонометрия зародилась в странах древнего Востока и, будучи тесно связанной с астрономией,сделала первые шаги в своем
- 7. Греческие астрономы
- 9. Сам термин косинус появился значительно позднее в работах европейских ученых впервые в конце XVI в.из так
- 11. Сирийский астроном ал-Баттани (Хв.) вычислил небольшую таблицу котангенсов через 1°
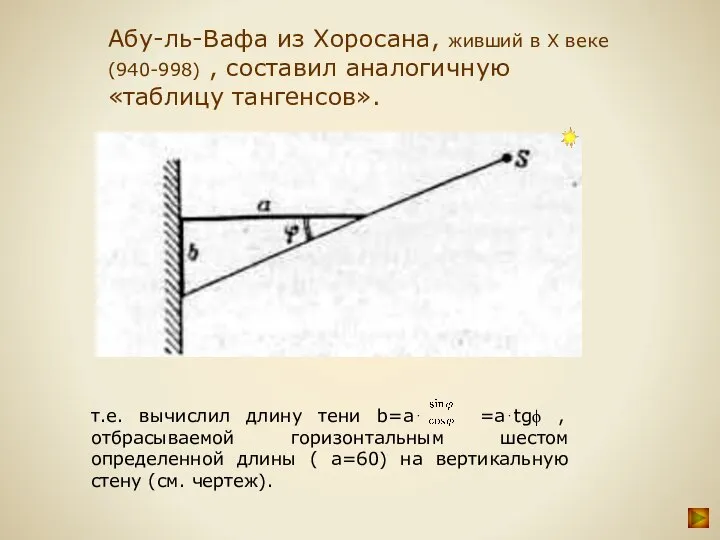
- 12. Абу-ль-Вафа из Хоросана, живший в Х веке (940-998) , составил аналогичную «таблицу тангенсов».
- 16. Основоположник аналитической теории тригонометрических функций.
- 17. В XIX веке продолжил развитие теории тригонометрических функций.
- 18. В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть-учение о тригонометрических
- 19. Прикладная направленность тригонометрии
- 20. Задача на применение винтовой линии .
- 21. Исследование движения ползуна в кривошипно-шатунном механизме. В начальный момент, когда кривошип занимает положение ОА1, точка В
- 22. Расчет длины ременной передачи, соединяющей два шкива: ведущий и ведомый. Пусть расстояние между центрами шкивов равно
- 23. Тригонометрия в артиллерии
- 24. Определение коэффициента трения. = .(2) . .
- 25. Зависимость между угловой и линейной скоростями По этой формуле можно находить линейную скорость точки, зная угловую
- 26. Соединение двух труб
- 27. Периодические процессы и колебания в окружающем мире
- 28. Гармонические колебания Одним из простейших видов колебаний является движение по оси проекции точки М, которая равномерно
- 29. Если мы сначала оттянем гирю на s0 см,а потом толкнем ее со скоростью v0, то она
- 30. Колебания маятника Чем длиннее маятник, тем медленнее он качается Изменение начального отклонения влияет на амплитуду колебаний
- 31. Разряд конденсатора
- 32. у=arcsin(sinx) ;
- 33. у=m·arcsin(sin k(x-α)). k=2 α=0 m=1; -2 ;0,5
- 34. Полярные координаты При решении многих задач удобнее пользоваться так называемыми полярными координатами: на плоскости выбирают неподвижную
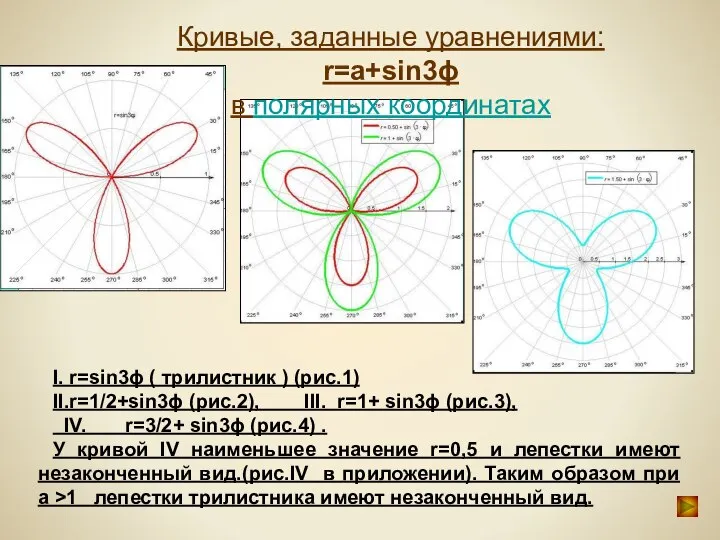
- 35. I. r=sin3ϕ ( трилистник ) (рис.1) II.r=1/2+sin3ϕ (рис.2), III. r=1+ sin3ϕ (рис.3), IV. r=3/2+ sin3ϕ (рис.4)
- 36. Уравнения, найденные немецким математиком-натуралистом Хабенихтом для геометрических форм, встречающихся в мире растений. Например, уравнениям r=4(1+cos3ϕ) и
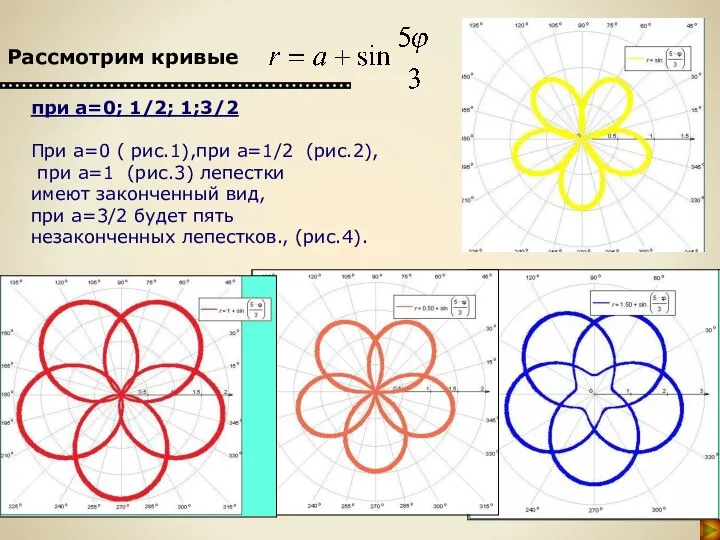
- 41. при а=0; 1/2; 1;3/2 При а=0 ( рис.1),при а=1/2 (рис.2), при а=1 (рис.3) лепестки имеют законченный
- 42. Кривые Лиссажу. Кривые Лиссажу, характеризуемые в общем случае уравнениями: В общем случае кривая располагается внутри прямоугольника
- 43. Замена уравнений : x=sin3t; y=sin 5t уравнениями: x=sin 3t; y=sin5(t+3) превращает незамкнутую кривую в кривую замкнутую.
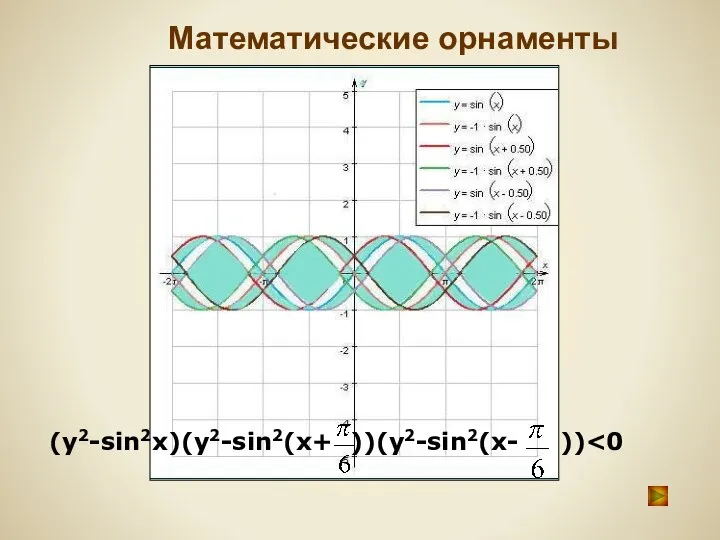
- 44. Математические орнаменты
- 45. Решение системы неравенств Решение неравенства (y-sinx)(y+sinx) Математические орнаменты
- 46. Математические орнаменты
- 47. КРОССВОРД 1. Наука об измерении треугольников 2.Автор работы «Пять книг о треугольниках всех видов» в XVI-XVII
- 48. КРОССВОРД
- 50. Скачать презентацию











































 Геометрическе преобразования
Геометрическе преобразования Задачка по математике Прогулка
Задачка по математике Прогулка Тренажёр «Помоги Снеговику». Математика 1 класс
Тренажёр «Помоги Снеговику». Математика 1 класс Чтение графиков, диаграмм, таблиц
Чтение графиков, диаграмм, таблиц Презентация по математике "Решение отдельных видов уравнений n-й степени ( n>2)" - скачать
Презентация по математике "Решение отдельных видов уравнений n-й степени ( n>2)" - скачать  Деление с остатком на 10, 100 и 1000
Деление с остатком на 10, 100 и 1000 Заслуженный учитель РФ, учитель математики, зам. дир. по физ.-мат. отделению московской гимназии 1543 на Юго-Западе, автор учебников ма
Заслуженный учитель РФ, учитель математики, зам. дир. по физ.-мат. отделению московской гимназии 1543 на Юго-Западе, автор учебников ма Проценты. Как найти число по его проценту
Проценты. Как найти число по его проценту Аттестационная работа. Рисуем на координатной плоскости
Аттестационная работа. Рисуем на координатной плоскости Если я знаю, что знаю мало, я добьюсь того, чтобы знать больше
Если я знаю, что знаю мало, я добьюсь того, чтобы знать больше Понятие предела функции
Понятие предела функции Число π (пи)
Число π (пи) Графический способ решения систем уравнений с двумя переменными
Графический способ решения систем уравнений с двумя переменными Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом Разложение многочлена на множители с помощью комбинации различных приемов 7 класс
Разложение многочлена на множители с помощью комбинации различных приемов 7 класс  Неравенство треугольника
Неравенство треугольника Презентация по математике Свойства корня n-ой степени
Презентация по математике Свойства корня n-ой степени Касательная к окружности
Касательная к окружности Коллекция задач. Первый признак подобия треугольников
Коллекция задач. Первый признак подобия треугольников Деление на двузначное число 7 класс - презентация_
Деление на двузначное число 7 класс - презентация_ Системы двух уравнений с двумя переменными
Системы двух уравнений с двумя переменными Электронные методические материалы на тему: «Золотое сечение» для учащихся 5-6 классов
Электронные методические материалы на тему: «Золотое сечение» для учащихся 5-6 классов Симметрия вокруг нас
Симметрия вокруг нас Экономические задачи. Подготовка к ОГЭ по математике
Экономические задачи. Подготовка к ОГЭ по математике Перевод десятичной дроби в обыкновенную дробь
Перевод десятичной дроби в обыкновенную дробь Презентация по математике "Обобщающий урок по теме «Четырехугольники»" - скачать
Презентация по математике "Обобщающий урок по теме «Четырехугольники»" - скачать  Выделение целой части из неправильной дроби
Выделение целой части из неправильной дроби Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2
Открытый интенсив по математике. Как мощно подготовиться к экзамену? Ценность времени. День 2