Содержание
- 2. Содержание 1.Теоремы о дифференцируемых функциях. 2. Правило Лопиталя раскрытия неопределенностей. 3.Убывание и возрастание функции. 4. Экстремумы.
- 3. Некоторые теоремы о дифференцируемых функциях
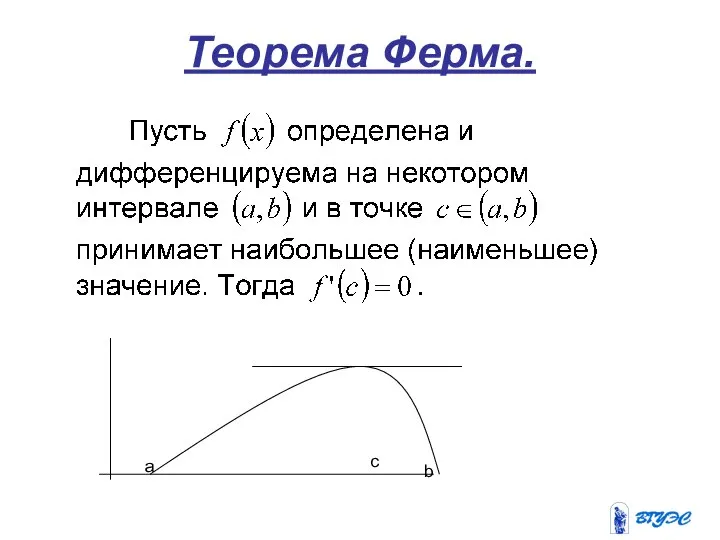
- 4. Теорема Ферма. a c b
- 5. Теорема Ролля.
- 6. Теорема Лагранжа.
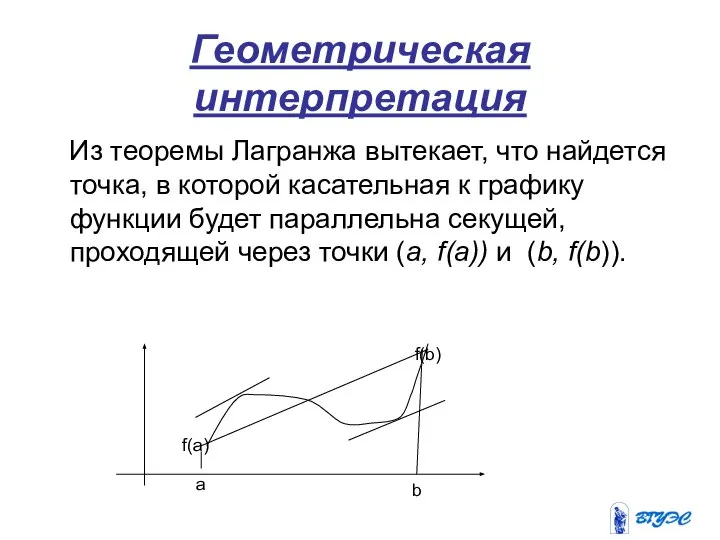
- 7. Геометрическая интерпретация Из теоремы Лагранжа вытекает, что найдется точка, в которой касательная к графику функции будет
- 8. Правило Лопиталя Пусть в некоторой окрестности О точки функции дифференцируемы всюду, кроме быть может самой точки
- 9. Правило Лопиталя Если функции являются одновременно бесконечно малыми или бесконечно большими при и при этом существует
- 10. Примеры. Правило применимо и в случае, когда 1. 2.
- 11. Примеры Найдем
- 12. Пример Найдем Прологарифмируем это выражение и найдем предел. Тогда
- 13. Убывающие и возрастающие функции
- 14. Теорема (Признак возрастания функции).
- 15. Теорема (Признак убывания функции).
- 16. Максимум и минимум функции
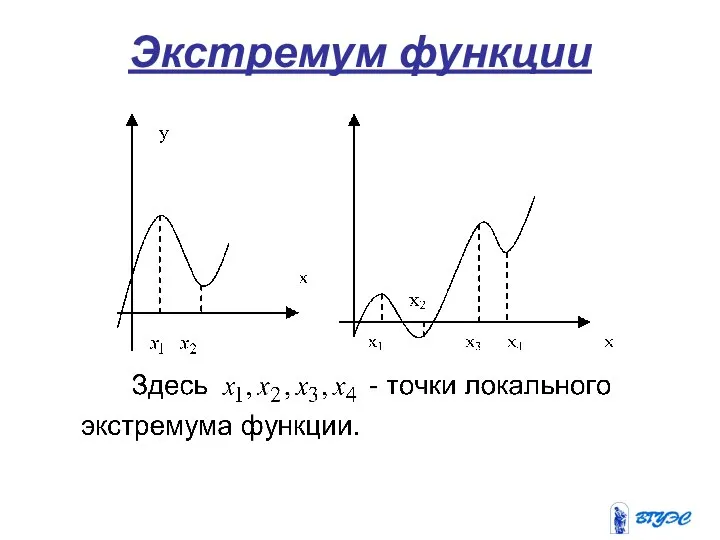
- 17. Экстремум функции
- 18. Экстремум функции
- 19. Необходимое условие экстремума Теорема. Если дифференцируемая функция имеет в точке с экстремум, то ее производная обращается
- 20. Экстремум функции
- 21. Продолжение Кроме точек, где , экстремумы могут быть в точках, где производная не существует или равна
- 22. Критические точки
- 23. Критические точки
- 24. Теорема (Достаточное условие экстремума).
- 25. Найти экстремумы Приравняем производную к нулю: Проверим, меняет ли производная знаки при переходе через эти точки,
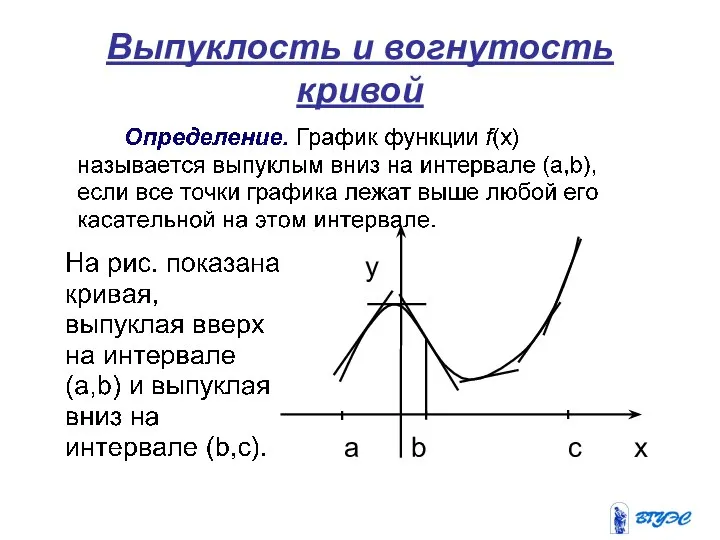
- 26. Выпуклость и вогнутость кривой
- 27. Достаточное условие выпуклости
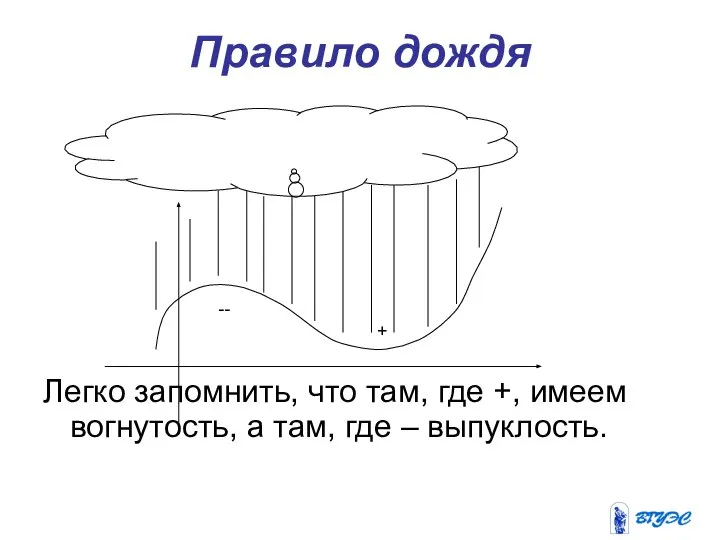
- 28. Правило дождя Легко запомнить, что там, где +, имеем вогнутость, а там, где – выпуклость. +
- 29. Точка перегиба
- 30. Достаточное условие перегиба кривой
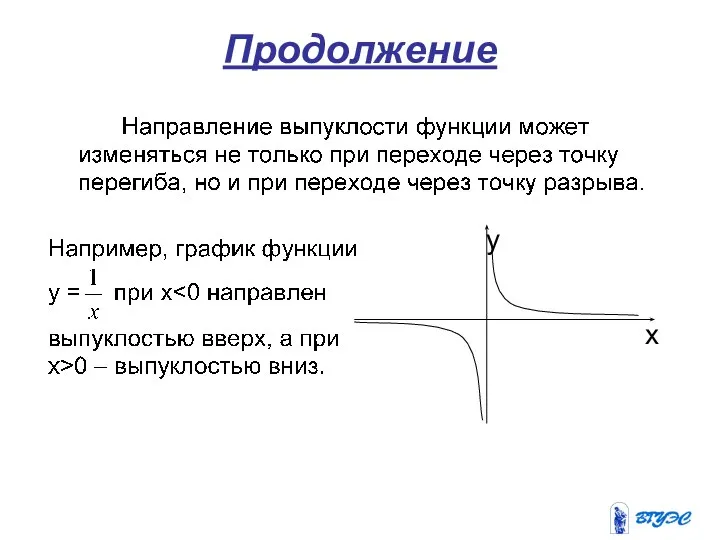
- 31. Продолжение
- 32. Асимптоты При исследовании формы кривой приходится исследовать характер изменения функции при неограниченном возрастании (по абсолютной величине)
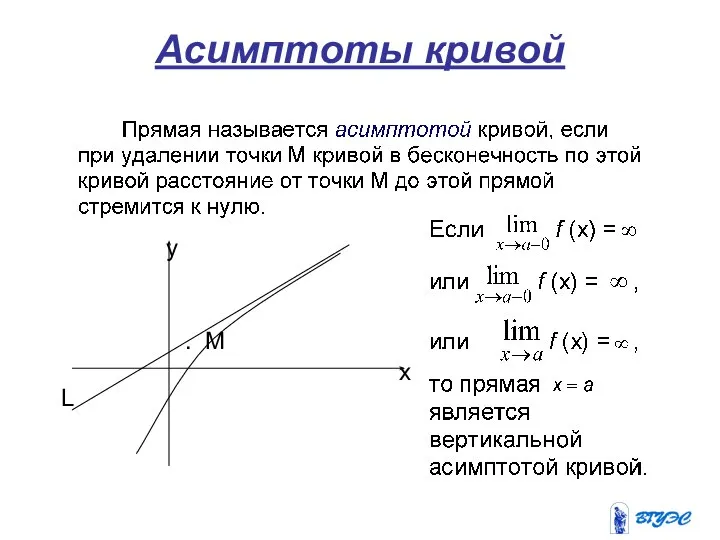
- 33. Асимптоты кривой
- 34. Пример Функция у = в точках х = 2, очевидно, имеет бесконечный разрыв, поэтому прямые х
- 35. Наклонные асимптоты Наклонные асимптоты задают уравнением у = kх + b, где угловой коэффициент k и
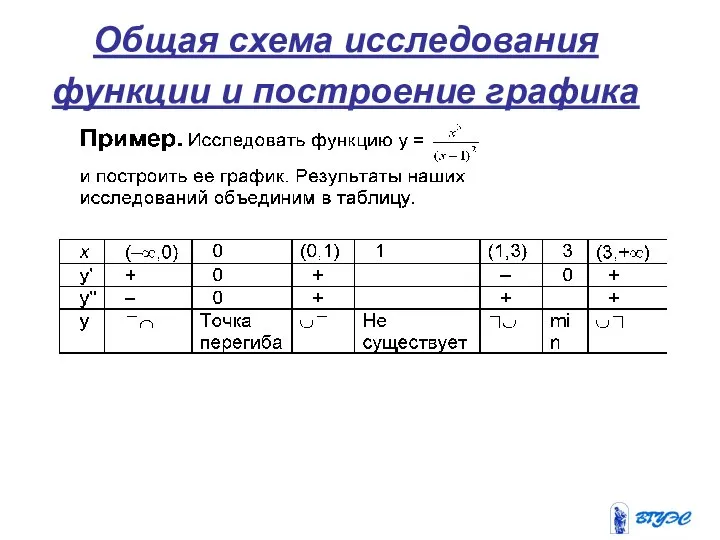
- 36. Общая схема исследования функции и построение графика
- 37. Общая схема исследования функции и построение графика
- 39. Скачать презентацию




























 Графики функций. 9 класс
Графики функций. 9 класс Комплексные числа
Комплексные числа Розв'язування трикутників
Розв'язування трикутників Презентация к уроку математики: «Натуральные числа и действия над ними» 5 класс Учитель математики
Презентация к уроку математики: «Натуральные числа и действия над ними» 5 класс Учитель математики  Презентация по математике "Нестандартные задачи" - скачать
Презентация по математике "Нестандартные задачи" - скачать  Десятичные дроби : сложение , вычитание , сравнение, округление, умножение на натуральное число
Десятичные дроби : сложение , вычитание , сравнение, округление, умножение на натуральное число Решение задач на применение свойств прямоугольных треугольников
Решение задач на применение свойств прямоугольных треугольников Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Случаи деления вида 80:20
Случаи деления вида 80:20 Окружность и круг. Сфера и шар
Окружность и круг. Сфера и шар Презентация на тему Метод математической индукции
Презентация на тему Метод математической индукции  Решение примеров
Решение примеров Дифференциальные уравнения
Дифференциальные уравнения Презентация по математике "Бенефис дробей" - скачать
Презентация по математике "Бенефис дробей" - скачать  Прямая в пространстве
Прямая в пространстве  Числовые промежутки. 8 класс
Числовые промежутки. 8 класс Своя игра. Дроби десятичные и обыкновенные. Игра для развития серых клеточек
Своя игра. Дроби десятичные и обыкновенные. Игра для развития серых клеточек Презентацию на тему:«Волшебный квадрат» Презентацию на тему:«Волшебный квадрат» подготовила ученица 9 класса МОУ СОШ п.Красно
Презентацию на тему:«Волшебный квадрат» Презентацию на тему:«Волшебный квадрат» подготовила ученица 9 класса МОУ СОШ п.Красно Презентация на тему Математический диктант 1 класс
Презентация на тему Математический диктант 1 класс  Сложение и вычитание смешанных чисел
Сложение и вычитание смешанных чисел Биквадрат теңдеу
Биквадрат теңдеу Нахождение оптимального сочетания пар объектов по заданным параметрам
Нахождение оптимального сочетания пар объектов по заданным параметрам Урок математики, 2 класс «Проверка вычитания»
Урок математики, 2 класс «Проверка вычитания»  Решение задач в тестовой форме
Решение задач в тестовой форме Протилежні числа
Протилежні числа Приближенные решения уравнений
Приближенные решения уравнений Специальная теория относительности (СТО) 1. Противоречия 2. Опыт Майкельсона–Морли 3. Постулаты Эйнштейна 4. Преобразования Ло
Специальная теория относительности (СТО) 1. Противоречия 2. Опыт Майкельсона–Морли 3. Постулаты Эйнштейна 4. Преобразования Ло Преобразование алгебраических выражений
Преобразование алгебраических выражений