Содержание
- 2. Содержание Сер Иссак Ньютон Математический анализ Дифференциальное исчисление (интегральное исчисление) Теория Ньютона-Лейблица
- 3. Тема проекта: «Изучение применения работ Ньютона в области математики» Актуальность исследовательской работы: Благодаря изучению работ Ньютона
- 4. Введение Математика -фундаментальная наука, предоставляющая (общие) языковые средства другим наукам; тем самым она выявляет их структурную
- 5. Сер Иссак ньютон Исаак Ньютон( 1642 года - 1727 года) - английский физик, математик, механик и
- 6. Математический анализ Математический анализ - совокупность разделов математики, соответствующих историческому разделу под наименованием «анализ бесконечно алых»,
- 7. Дифференциальное исчисление Дифференциальное исчисление изучает определение, свойства и применение производных функций. Процесс нахождения производной называется дифференцированием.
- 8. Интегральное исчисление Интегральное исчисление — это изучение определения, свойств и применения двух взаимосвязанных понятий: неопределённого интеграла
- 9. Теорема Ньютона-Лейблица Теорема Ньютона — Лейбница, которую также называют основной теоремой анализа утверждает, что дифференцирование и
- 10. Список используемых источников 1.Иссак Ньютон:-https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7 2. Математический анализ:- https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7 3. Дифференцированное исчисление:-https://www.nehudlit.ru/books/detail1183272.html 4.Интегральное исчисление:- https://yunc.org/%D0%98%D1%81%D0%B0%D0%B0%D0%BA_%D0%9D%D1%8C%D1%8E%D1%82%D0%BE%D0%BD,_%D1%80%D0%B0%D0%B7%D0%B4%D0%B5%D0%BB_%C2%AB%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%C2%BB 5.Теория
- 12. Скачать презентацию









 Урок математики в 11 классе
Урок математики в 11 классе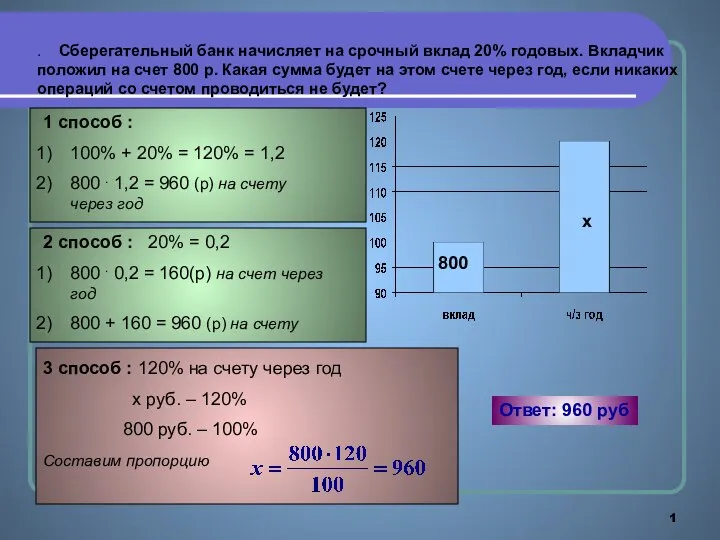 Задачи на проценты
Задачи на проценты Деление двузначного числа на двузначное (3 класс)
Деление двузначного числа на двузначное (3 класс) Лабороторная работа 2 ВТ 20-1
Лабороторная работа 2 ВТ 20-1 Статистические критерии различий. Непараметрические критерии для связных выборок
Статистические критерии различий. Непараметрические критерии для связных выборок Статистические оценки параметров распределения. Доверительные интервалы
Статистические оценки параметров распределения. Доверительные интервалы Задача и алгоритм Прима
Задача и алгоритм Прима Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Проценты
Проценты Презентация по математике "Способы умножения" - скачать
Презентация по математике "Способы умножения" - скачать  Золотое сечение
Золотое сечение Золотое сечение в живой природе
Золотое сечение в живой природе Решение заданий № 21 II части ГИА-2014
Решение заданий № 21 II части ГИА-2014 Преобразование выражений, содержащих радикалы
Преобразование выражений, содержащих радикалы Модели систем. Лекция 3
Модели систем. Лекция 3 Криптография, математические алгоритмы при шифровании. Муниципальное общеобразовательное учреждение «Лицей города Троицка»
Криптография, математические алгоритмы при шифровании. Муниципальное общеобразовательное учреждение «Лицей города Троицка» Параллелепипед. Куб
Параллелепипед. Куб Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Учимся решать тригонометрические неравенства
Учимся решать тригонометрические неравенства Раньше, позже, сначала, потом
Раньше, позже, сначала, потом Арифметический квадратный корень
Арифметический квадратный корень Построение и анализ частотных характеристик СУ
Построение и анализ частотных характеристик СУ Модифицированное число единиц переноса.(лекция 5)
Модифицированное число единиц переноса.(лекция 5) Тригонометрическая форма записи комплексного числа
Тригонометрическая форма записи комплексного числа Правильные многогранники
Правильные многогранники Действия с десятичными дробями. Обобщающий урок
Действия с десятичными дробями. Обобщающий урок Математика 1 класс I полугодие I четверть Раздел: «Подготовка к изучению чисел и действий с ними» к УМК М. И. Моро, C. И. Волков
Математика 1 класс I полугодие I четверть Раздел: «Подготовка к изучению чисел и действий с ними» к УМК М. И. Моро, C. И. Волков Сложение дробей. Прикидка и оценка результата
Сложение дробей. Прикидка и оценка результата