Содержание
- 2. Виды статистических ошибок Интервальные оценки Доверительные интервалы
- 3. Виды статистических ошибок Def: Статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
- 4. Def: Несмещенной называют статистическую оценку Θ*, математическое ожидание которой равно оцениваемому параметру Θ при любом объеме
- 5. Def: Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру. Оценки бывают
- 6. Точечные оценки
- 7. При выборке малого объема точечная оценка может разительно отличаться от оцениваемого параметра, т.е. приводить к грубым
- 8. Интервальные оценки Интервальные оценки позволяют установить точность и надежность оценок. Пусть найденная по данным выборки статистическая
- 9. Т.о., положительное число δ характеризует точность оценки. Однако статистические методы не позволяют категорически утверждать, что оценка
- 10. Def: Надежностью (доверительной вероятностью) оценки Θ по Θ* называют вероятность γ, с которой осуществляется неравенство │Θ
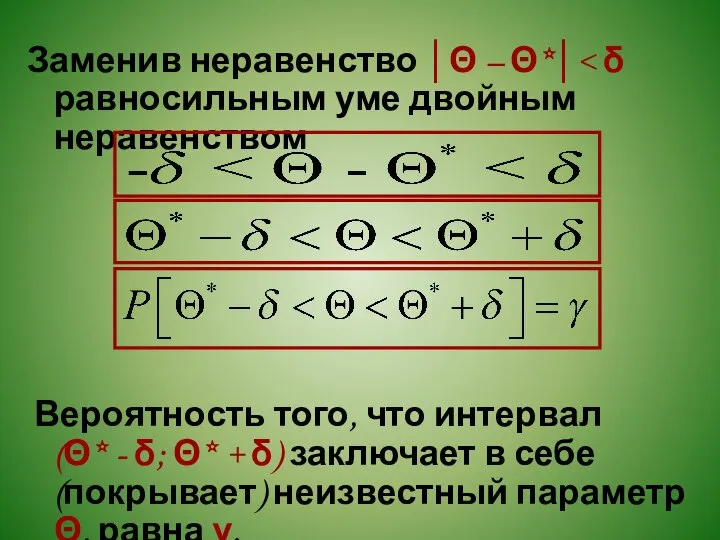
- 11. Заменив неравенство │Θ – Θ*│ Вероятность того, что интервал (Θ* - δ; Θ* + δ) заключает
- 12. Доверительный интервал Def: Доверительным интервалом называется случайный интервал (Q* - δ; O* + δ), в пределах
- 13. Доверительный интервал для математического ожидания нормально распределенного признака с известным средним квадратическим отклонением находят по формуле:
- 14. Приведенная формула позволяет решать следующие задачи: 1) По заданным надежности γ и объеме выборки n находить
- 15. В случае большой выборки при n > 30 и неизвестном среднем квадратическом отклонении σ(X) доверительный интервал
- 16. Исследование большой выборки может оказаться невозможным по различным признакам. Кроме этого, с уменьшением n доверительный интервал
- 17. Эта величина соответствует закону t – распределения Стьюдента. Дифференциальная функция распределения T обозначается S(tγ; n) и
- 18. Вероятность попадания случайной величины в соответствующий интервал равна:
- 19. Доверительный интервал для оценки математического ожидания при неизвестном σ. где tγ = t(γ; n) – числа,
- 20. Примечание: при большом объеме выборки (n ≥ 30) значения tγ таблицы Стьюдента и t таблицы Лапласа
- 21. Пример Для определения средней живой массы трехмесячного теленка определенной породы были взвешены 100 животных и результаты
- 22. Найти: величины, которые следует принять за среднюю массу и среднее квадратическое отклонение; ошибку средней и коэффициетнт
- 23. Решение 1) В качестве приближенного значения средней массы принимаем выборочную среднюю, а за значение признака –
- 24. Вычисляем выборочную исправленную дисперсию
- 25. Находим исправленное выборочное среднее квадратичное отклонение
- 26. 2) Ошибка средней равна Коэффициент вариации показывает, что изменчивость признака средняя.
- 27. 3) Поскольку n = 100 > 30 и у нас случай нормального распределения, то доверительный интервал
- 28. Из условия 2Φ(tγ) = 0.95 определяем Φ(tγ) = 0,475, а по таблице приложений находим tγ =
- 29. Замечание: если требуется оценить математическое ожидание с наперед заданной точностью δ и надежностью γ, то максимальный
- 30. Объем выборочной совокупности при повторном способе отбора находят по формуле: где параметр t определяют из по
- 31. Доверительный интервал для оценки среднего квадратического отклонения σ нормального распределения.
- 33. Скачать презентацию





























 Исследовательская работа. Тема:Уравнения и неравенства, содержащие знак модуля
Исследовательская работа. Тема:Уравнения и неравенства, содержащие знак модуля Тест по теме: Комбинация фигур
Тест по теме: Комбинация фигур Числовые функции, свойства функции, 10 класс
Числовые функции, свойства функции, 10 класс Произведение многочленов
Произведение многочленов Множество. Элемент множества.
Множество. Элемент множества.  Зеркальная симметрия
Зеркальная симметрия  Четырехугольники
Четырехугольники Сопряжение. Геометрические построения
Сопряжение. Геометрические построения Тест по теме: "Координаты точки и координаты вектора"
Тест по теме: "Координаты точки и координаты вектора" Муниципальное образовательное учреждение «Гимназия №20» секция теоретической математики Автор: Буравлев Степан, 10 физико-матем
Муниципальное образовательное учреждение «Гимназия №20» секция теоретической математики Автор: Буравлев Степан, 10 физико-матем Подготовка к ЕГЭ. Графическое решение уравнений и неравенств
Подготовка к ЕГЭ. Графическое решение уравнений и неравенств Франсуа Виет
Франсуа Виет Разложение квадратного трехчлена на множители
Разложение квадратного трехчлена на множители Метод Монте-Карло: моделирование дискретной случайной величины
Метод Монте-Карло: моделирование дискретной случайной величины Координатная плоскость. 6 класс
Координатная плоскость. 6 класс Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей
Взаимные положения прямой и плоскости, двух плоскостей. Параллельность прямой и плоскости; двух плоскостей Логарифмические неравенства
Логарифмические неравенства Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Готовимся к Всероссийским проверочным работам по математике
Готовимся к Всероссийским проверочным работам по математике Разгадать ребус
Разгадать ребус Показатели вариации
Показатели вариации Нормальний закон розподілу у сукупностях
Нормальний закон розподілу у сукупностях Презентация по математике "Пифагор. За легендой - Истина" - скачать
Презентация по математике "Пифагор. За легендой - Истина" - скачать  Дружественные, фигурные и совершенные числа, теория чисел
Дружественные, фигурные и совершенные числа, теория чисел Измерение углов на местности
Измерение углов на местности Арккосинус. Решение уравнения cos x=a
Арккосинус. Решение уравнения cos x=a Решение задач на применение первого признака равенства треугольников
Решение задач на применение первого признака равенства треугольников Задачи по геометрии
Задачи по геометрии