Слайд 19

Здесь m — количество уравнений, а n — количество переменных, x1,
x2, … , xn — неизвестные, которые надо определить, коэффициенты a11, a12, … , amn и свободные члены b1, b2, … , bm предполагаются известными. Индексы коэффициентов в системах линейных уравнений (aij) формируются по следующему соглашению: первый индекс (i) обозначает номер уравнения, второй (j) — номер переменной, при которой стоит этот коэффициент.
Система называется однородной, если все её свободные члены равны нулю (b1= b2= … = bm = 0), иначе — неоднородной.
Квадратная система линейных уравнений — система, у которой количество уравнений совпадает с числом неизвестных (m=n). Система, у которой число неизвестных больше числа уравнений является недоопределённой, такие системы линейных алгебраических уравнений также называются прямоугольными. Если уравнений больше, чем неизвестных, то система является переопределённой.
Решение системы линейных алгебраических уравнений — совокупность n чисел c1, c2, … , cn, таких что их соответствующая подстановка вместо x1, x2, … , xn в систему обращает все её уравнения в тождества.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения. Решения считаются различными, если хотя бы одно из значений переменных не совпадает. Совместная система с единственным решением называется определённой, при наличии более одного решения — недоопределённой.






















 Сформулировать результат выполнения фрагмента (функции) и определить роль переменной – счетчика
Сформулировать результат выполнения фрагмента (функции) и определить роль переменной – счетчика Теория графов
Теория графов Интерактивный плакат: Объём пирамиды
Интерактивный плакат: Объём пирамиды Сложение двузначных чисел урок - сказка
Сложение двузначных чисел урок - сказка  Тригонометрические функции. Тангенс и котангенс
Тригонометрические функции. Тангенс и котангенс Устный счёт
Устный счёт Устные задачи на готовых чертежах. Смежные и вертикальные углы
Устные задачи на готовых чертежах. Смежные и вертикальные углы Вычисление интегралов
Вычисление интегралов Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии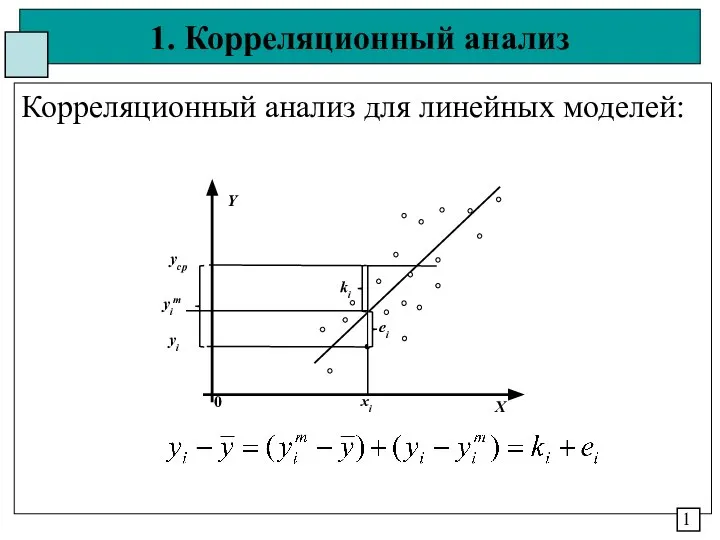 Корреляционный анализ для линейных моделей
Корреляционный анализ для линейных моделей Аттестационная работа. Эссе. Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС
Аттестационная работа. Эссе. Проектно-исследовательская деятельность на уроках математики в условиях реализации ФГОС Одночлены и их свойства
Одночлены и их свойства Квадрат одночлена
Квадрат одночлена Тождества. Переместительное свойство
Тождества. Переместительное свойство Условная оптимизация. Лекция 11
Условная оптимизация. Лекция 11 Адаптивные фильтры. Практическое применение (3)
Адаптивные фильтры. Практическое применение (3) Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Оценки рисков
Оценки рисков Прямоугольный параллелепипед
Прямоугольный параллелепипед Итоговый контрольный тест по геометрии, 7 класс
Итоговый контрольный тест по геометрии, 7 класс Делители и кратные
Делители и кратные Основы математического моделирования в землеустройстве
Основы математического моделирования в землеустройстве Смежные и вертикальные углы
Смежные и вертикальные углы Формализованные методы прогнозирования
Формализованные методы прогнозирования Математичні моделі та методи теорії портфеля
Математичні моделі та методи теорії портфеля Пентамино. Игра-головоломка
Пентамино. Игра-головоломка Обобщающий урок по теме «Соотношения между сторонами и углами треугольника»
Обобщающий урок по теме «Соотношения между сторонами и углами треугольника» Цилиндр
Цилиндр