Содержание
- 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ Ряд распределения. Многоугольник распределения Законом распределения случайной величины называется всякое
- 3. Рассмотрим прерывную случайную величину X с возможными значениями x1, х2, …, хn. Каждое из этих значений
- 4. Ряд распределения случайной величины X имеет следующий вид Чтобы придать ряду распределения более наглядный вид, часто
- 5. Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину; он является одной из
- 6. Функция распределения Для количественной характеристики распределения вероятностей удобно воспользоваться не вероятностью события Х=х, а вероятностью события
- 7. Функция распределения F(x) иногда называют также интегральной функцией распределения или интегральным законом распределения. Функция распределения –
- 8. Сформулируем некоторые общие свойства функции распределения. Функция распределения F(x) есть неубывающая функция своего аргумента, т. е.
- 9. График функции распределения вероятностей.
- 10. Не давая строгого доказательства этих свойств, проиллюстрируем их с помощью наглядной геометрической интерпретации. Для этого будем
- 11. Плотность распределения Функция f(x) – произвольная функция распределения характеризует как бы плотность, с которой распределяются значения
- 12. Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.
- 13. Плотность распределения, так же как и функция распределения, есть одна из форм закона распределения. В противоположность
- 14. Рассмотрим непрерывную случайную величину X с плотностью распределения f(х) и элементарный участок dх, примыкающий к точке
- 16. Выразим вероятность попадания величины X на отрезок от α до β через плотность распределения. Очевидно, она
- 17. Основные свойства плотности распределения. Плотность распределения есть неотрицательная функция: Это свойство непосредственно вытекает из того, что
- 18. Геометрически основные свойства плотности распределения означают, что: вся кривая распределения лежит не ниже оси абсцисс; 2)
- 19. Математическое ожидание Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности
- 20. Для непрерывной случайной величины Х математическое ожидание выражается уже не суммой, а интегралом: где f(x) –
- 21. МОМЕНТЫ Понятие момента широко применяется в механике для описания распределения масс. Совершенно теми же приемами пользуются
- 22. Начальный момент Начальным моментом s-го порядка прерывной случайной величины Х называется сумма вида: Для непрерывной случайной
- 23. Общее определение начального момента s-го порядка справедливое как для прерывных, так и для непрерывных величин: ,
- 24. Центральный момент Центральным моментом порядка s случайной величины Х называется математическое ожидание s-ой степени соответствующей центрированной
- 25. Дисперсия Из всех моментов в качестве характеристик случайной величины чаще всего применяются первый начальный момент (математическое
- 26. РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛНИЯ Случайная величина имеет равномерный закон распределения если ее значения в интервале одинаково равновероятны.
- 27. Равномерный закон распределения характеризуется плотностью вероятности вида:
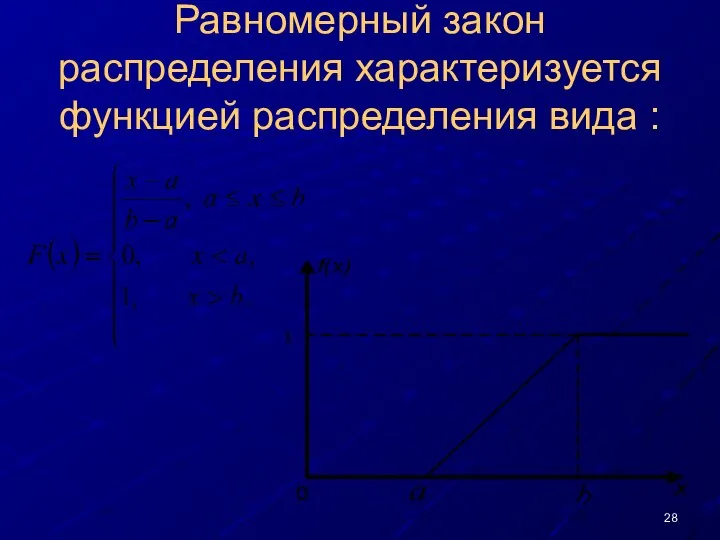
- 28. Равномерный закон распределения характеризуется функцией распределения вида :
- 29. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в теории
- 30. Кривая распределения, по нормальному закону имеет симметричный колоколообразный вид. Максимальная ордината кривой, равная соответствует точке х
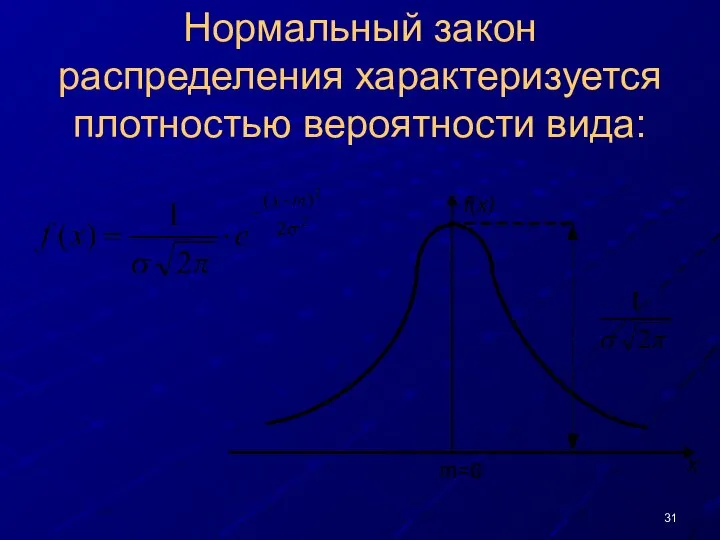
- 31. Нормальный закон распределения характеризуется плотностью вероятности вида:
- 32. Нормальный закон распределения характеризуется функцией распределения вида: - табулированный интеграл Лаплас
- 33. РЕЛЕЕВСКИЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Распределение модуля вектора на плоскости, координаты которого являются независимыми случайными величинами, что имеют
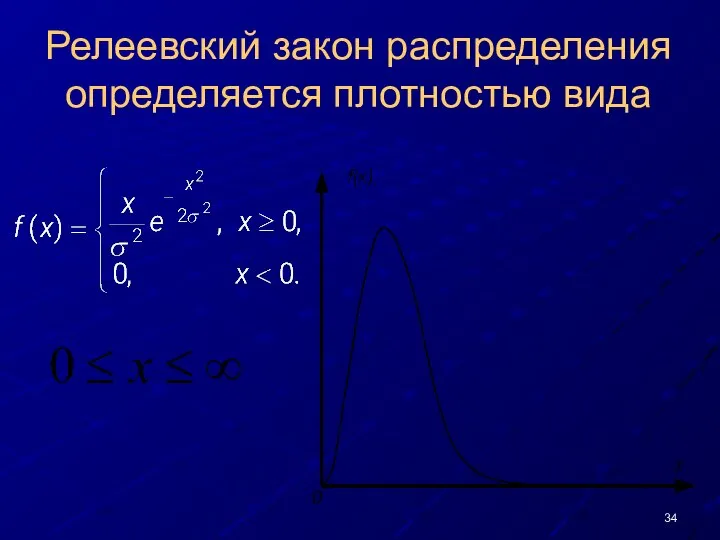
- 34. Релеевский закон распределения определяется плотностью вида
- 35. Релеевский закон распределения определяется функцией вида Плотности распределения соответствует функция распределения вероятностей при и равная при
- 37. Скачать презентацию































 Особенности построения фазовых портретов
Особенности построения фазовых портретов Собирательные числительные
Собирательные числительные Свойства функций . 9 класс
Свойства функций . 9 класс Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Вавилонская система счисления
Вавилонская система счисления Урок математики в 3классе. «Путешествие по Астане» подготовила учитель начальных классов Пак Светлана Александровна
Урок математики в 3классе. «Путешествие по Астане» подготовила учитель начальных классов Пак Светлана Александровна  Сравнение чисел. Урок математики в 6 классе
Сравнение чисел. Урок математики в 6 классе Симметрия в нашей жизни
Симметрия в нашей жизни Треугольники. Задачи
Треугольники. Задачи Решение задач методом координат. 5 класс
Решение задач методом координат. 5 класс Уравнения и способы их решения
Уравнения и способы их решения Презентация по математике "Учимся считать от 0 до 10" - скачать
Презентация по математике "Учимся считать от 0 до 10" - скачать  Наибольший общий делитель и наименьшее общее кратное
Наибольший общий делитель и наименьшее общее кратное Геометрические тела
Геометрические тела Преобразование подобия. Гомотетия
Преобразование подобия. Гомотетия Четырехугольники. Своя игра
Четырехугольники. Своя игра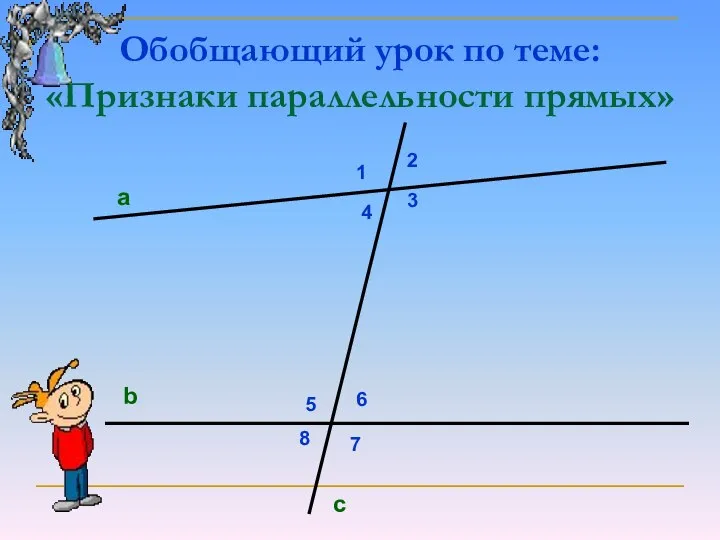 Обобщающий урок по теме: «Признаки параллельности прямых»
Обобщающий урок по теме: «Признаки параллельности прямых» Геометрические иллюзии
Геометрические иллюзии Решение задач на проценты. Как найти % от числа
Решение задач на проценты. Как найти % от числа Объем тела. Принцип Кавальери
Объем тела. Принцип Кавальери Презентация на тему Коэффициенты
Презентация на тему Коэффициенты  Математический аукцион. 9 класс
Математический аукцион. 9 класс Готовимся к итоговой аттестации
Готовимся к итоговой аттестации Обобщающий урок по теме: «Синус, косинус, тангенс суммы и разности аргументов. Презентация выполнена для уроков по алгебре и начал
Обобщающий урок по теме: «Синус, косинус, тангенс суммы и разности аргументов. Презентация выполнена для уроков по алгебре и начал Численное решение одномерных задач динамики сплошных сред с учетом симметрии
Численное решение одномерных задач динамики сплошных сред с учетом симметрии Задача линейного программирования, графический способ решения
Задача линейного программирования, графический способ решения Сюжетные задачи
Сюжетные задачи Различные способы умножения. Проектная работа
Различные способы умножения. Проектная работа