Содержание
- 2. Пример на направляющие косинусы Модуль вектора a равен 5. С осями координат Ox, Oy он образует
- 3. Пример на деление отрезков Найти длину медианы CD треугольника, заданного вершинами A(-1;2;5), B(3;0;1), C(2;3;4).
- 4. 6.1. Скалярное произведение векторов Скалярным произведением двух векторов называется число, равное произведению модулей векторов на косинус
- 5. Таблица скалярного умножения в декартовых координатах Запишем векторы a и b в виде суммы компонент: Тогда,
- 6. Свойства скалярного произведения. Из свойств сложения умножения действительных чисел Из определения скалярного произведения Из свойств скалярной
- 7. Условие ортогональности (из свойства 7): Или, в двумерном случае: Некоторые из свойств в декартовых координатах (пригодится
- 8. Проекция вектора на вектор (из свойства 4): Где используется скалярное произведение: нахождение модуля вектора или отрезка;
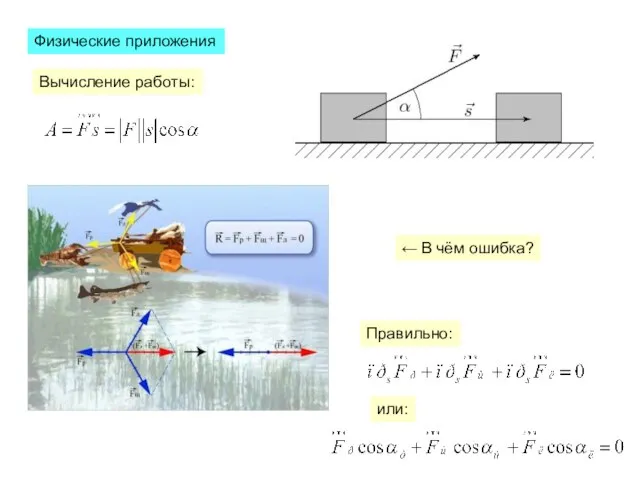
- 9. Физические приложения Вычисление работы: ← В чём ошибка? Правильно: или:
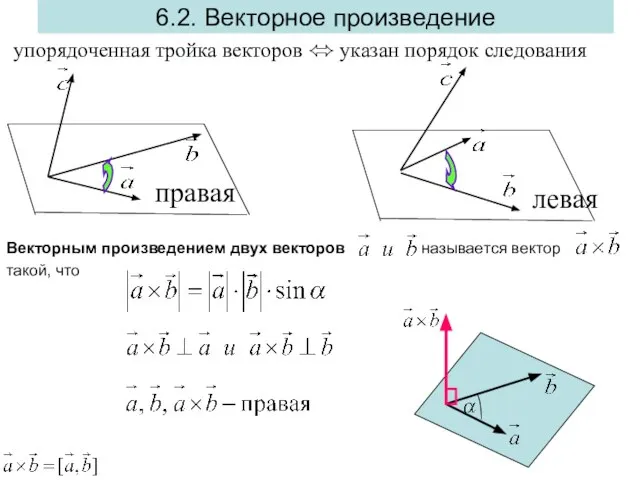
- 10. упорядоченная тройка векторов ⬄ указан порядок следования правая левая 6.2. Векторное произведение
- 11. Векторное произведение векторов в координатной форме
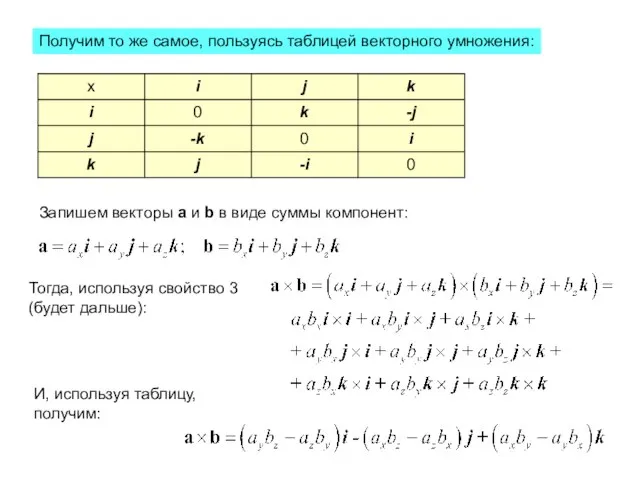
- 12. Получим то же самое, пользуясь таблицей векторного умножения: Запишем векторы a и b в виде суммы
- 13. Что, в свою очередь, сворачивается в сумму миноров: которая является разложением определителя 3-го порядка, т.е.
- 14. Свойства векторного произведения. Из свойств определителя Из определения векторного произведения и формулы площади Из свойств определителя
- 15. Некоторые из свойств в декартовых координатах (пригодится в задачках) Условие колинеарности двух векторов (из свойства 5):
- 16. Вычисление площади параллелограмма и треугольника (из свойства 4): Тогда:
- 17. Где используется векторное произведение: вычисление площади параллелограмма, треугольника и фигур, которые можно на них разбить; нахождение
- 18. Пример на нахождение площади треугольника Вычислить площадь треугольника, построенного на векторах p и q: p =
- 19. Пример на нахождение площади треугольника в декартовых координатах Вычислить площадь треугольника с вершинами в точках A(1;
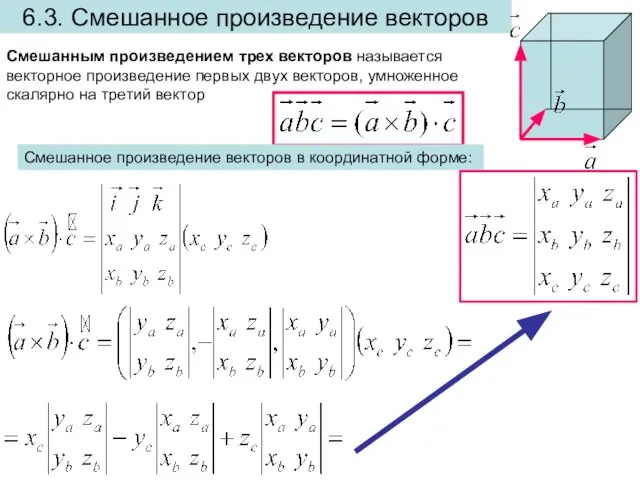
- 20. 6.3. Смешанное произведение векторов Смешанным произведением трех векторов называется векторное произведение первых двух векторов, умноженное скалярно
- 21. Свойства смешанного произведения. Из свойств определителя Из свойств определителя
- 22. Подробнее… Вычисление объёма параллелепипеда, призмы и пирамиды (свойство 3): Даны некомпланарные векторы b, c, a. Построим
- 23. Соответственно, для треугольной призмы: и для тетраэдра:
- 24. Условие компланарности трёх векторов (свойство 4): Пусть даны: a, b, c компланарны, если abc = 0.
- 25. Где используется смешанное произведение: вычисление объёмов геометрических тел, ограниченных плоскими гранями; решение геометрических задач, связанных с
- 26. Пример на вычисление объёма фигуры (смешанное произведение) Даны точки: A(2; 1; 3), B(1; 1; 4), C(3;
- 27. Задача на разложение вектора по базису Даны три вектора a = (2, -1), b = (1,
- 28. Пример на вычисление скалярного произведения Дано: |a| = 3, |b| = 4, (а) a2; (б) (3a
- 30. Скачать презентацию























 Тренажёр. Счёт 1 - 20
Тренажёр. Счёт 1 - 20 Применение векторов к решению задач
Применение векторов к решению задач Сложение и вычитание дробей с одинаковыми знаменателями
Сложение и вычитание дробей с одинаковыми знаменателями Задачи математической статистики
Задачи математической статистики Использование многофакторных моделей на основе главных компонент для прогнозирования состояния социально-экономических систем
Использование многофакторных моделей на основе главных компонент для прогнозирования состояния социально-экономических систем Соответствия и функции
Соответствия и функции Интегралы Эйлера первого и второго рода
Интегралы Эйлера первого и второго рода Как решать уравнения. 5 класс
Как решать уравнения. 5 класс Формула площади прямоугольника Математика 5 класс
Формула площади прямоугольника Математика 5 класс  Обобщение по теме "одночлены"
Обобщение по теме "одночлены" Универсальный тренажёр. Математика 2 класс
Универсальный тренажёр. Математика 2 класс Построение графика квадратичной функции
Построение графика квадратичной функции Презентация по математике "Задачи на прямоугольный параллелепипед" - скачать бесплатно
Презентация по математике "Задачи на прямоугольный параллелепипед" - скачать бесплатно Элементы теории поля
Элементы теории поля Основные задачи эконометрических исследований
Основные задачи эконометрических исследований Равные многоугольники
Равные многоугольники Тема урока: Раскрытие скобок.
Тема урока: Раскрытие скобок.  Свойства числовых неравенств
Свойства числовых неравенств Неделя математики
Неделя математики Вписанные и центральные углы
Вписанные и центральные углы Свойства и график функции косинуса y=cos x
Свойства и график функции косинуса y=cos x Решение уравнений. Раскрытие скобок
Решение уравнений. Раскрытие скобок Делители и кратные (часть 1)
Делители и кратные (часть 1) Объем пирамиды
Объем пирамиды Sampling in quantitative research
Sampling in quantitative research 2 класс Математический диктант № 2 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр
2 класс Математический диктант № 2 Выполнила Кирилова С.Г. Учитель начальных классов Школы «Ученики Пифагора» г. Лимассол, р.Кипр Компетентностно-ориентированные задания. Пропорции
Компетентностно-ориентированные задания. Пропорции Краткие сведения об аппроксимации функций
Краткие сведения об аппроксимации функций