Содержание
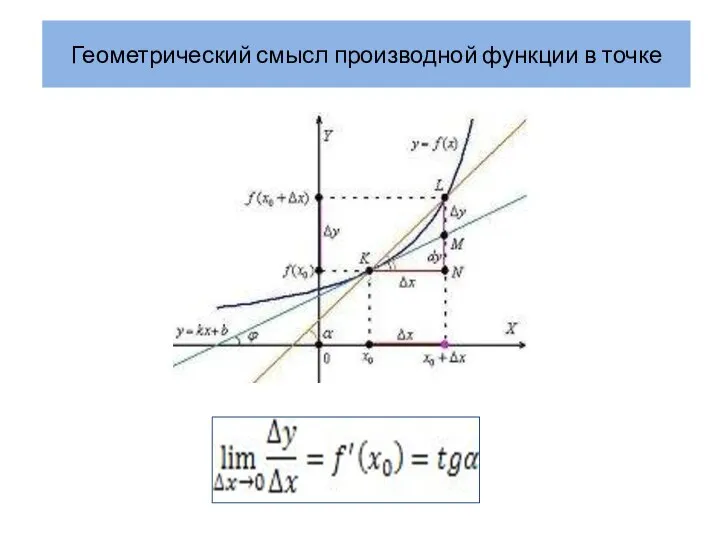
- 2. Геометрический смысл производной функции в точке
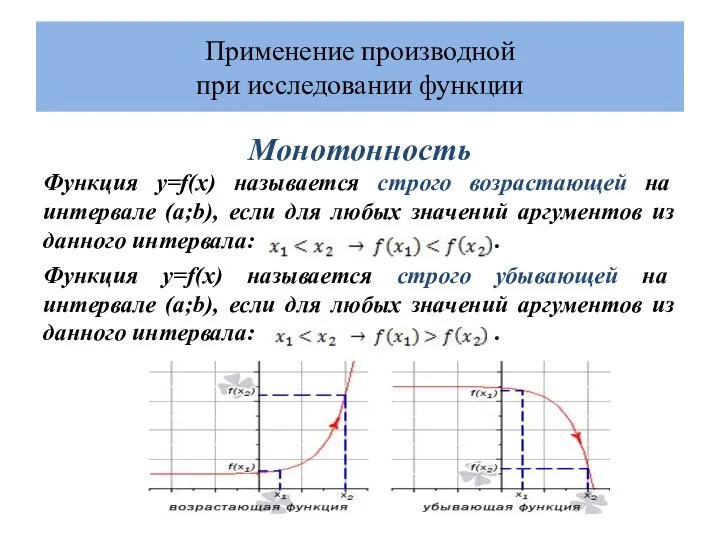
- 3. Применение производной при исследовании функции Монотонность Функция y=f(x) называется строго возрастающей на интервале (a;b), если для
- 4. Необходимые и достаточные условия монотонности функции Теорема 1. (Необходимое и достаточное условия возрастания функции) Если дифференцируемая
- 5. Алгоритм нахождения промежутков монотонности функции Для нахождения промежутки возрастания и убывания функции y=f(x) необходимо: найти область
- 6. Точки экстремума функции
- 7. Необходимое условие экстремума функции
- 8. Достаточное условие экстремума
- 10. Скачать презентацию





 Урок математики в 11 классе
Урок математики в 11 классе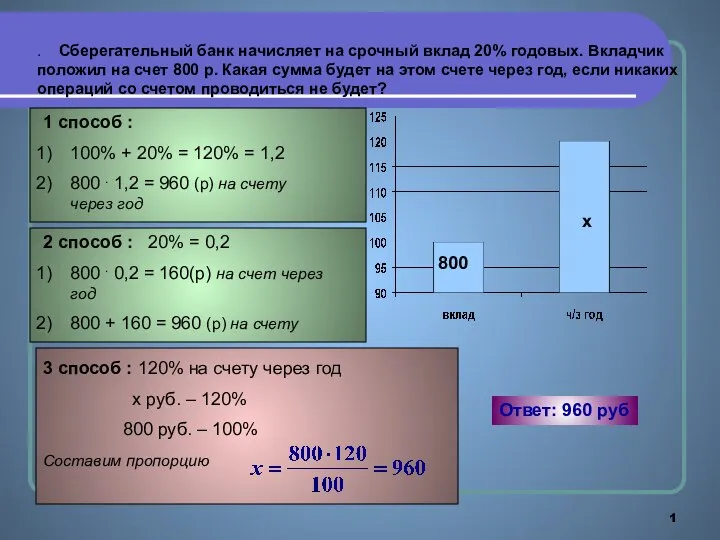 Задачи на проценты
Задачи на проценты Деление двузначного числа на двузначное (3 класс)
Деление двузначного числа на двузначное (3 класс) Лабороторная работа 2 ВТ 20-1
Лабороторная работа 2 ВТ 20-1 Статистические критерии различий. Непараметрические критерии для связных выборок
Статистические критерии различий. Непараметрические критерии для связных выборок Статистические оценки параметров распределения. Доверительные интервалы
Статистические оценки параметров распределения. Доверительные интервалы Задача и алгоритм Прима
Задача и алгоритм Прима Понятие дифференциала. Приложение дифференциала
Понятие дифференциала. Приложение дифференциала Проценты
Проценты Презентация по математике "Способы умножения" - скачать
Презентация по математике "Способы умножения" - скачать  Золотое сечение
Золотое сечение Золотое сечение в живой природе
Золотое сечение в живой природе Решение заданий № 21 II части ГИА-2014
Решение заданий № 21 II части ГИА-2014 Преобразование выражений, содержащих радикалы
Преобразование выражений, содержащих радикалы Модели систем. Лекция 3
Модели систем. Лекция 3 Криптография, математические алгоритмы при шифровании. Муниципальное общеобразовательное учреждение «Лицей города Троицка»
Криптография, математические алгоритмы при шифровании. Муниципальное общеобразовательное учреждение «Лицей города Троицка» Параллелепипед. Куб
Параллелепипед. Куб Круг. Окружность. Длина окружности. Площадь круга. 6 класс
Круг. Окружность. Длина окружности. Площадь круга. 6 класс Учимся решать тригонометрические неравенства
Учимся решать тригонометрические неравенства Раньше, позже, сначала, потом
Раньше, позже, сначала, потом Арифметический квадратный корень
Арифметический квадратный корень Построение и анализ частотных характеристик СУ
Построение и анализ частотных характеристик СУ Модифицированное число единиц переноса.(лекция 5)
Модифицированное число единиц переноса.(лекция 5) Тригонометрическая форма записи комплексного числа
Тригонометрическая форма записи комплексного числа Правильные многогранники
Правильные многогранники Действия с десятичными дробями. Обобщающий урок
Действия с десятичными дробями. Обобщающий урок Математика 1 класс I полугодие I четверть Раздел: «Подготовка к изучению чисел и действий с ними» к УМК М. И. Моро, C. И. Волков
Математика 1 класс I полугодие I четверть Раздел: «Подготовка к изучению чисел и действий с ними» к УМК М. И. Моро, C. И. Волков Сложение дробей. Прикидка и оценка результата
Сложение дробей. Прикидка и оценка результата