Содержание
- 2. 1. Вычислимые функции
- 3. Каждый алгоритм задает функцию, поскольку по набору исходных данных выдает результат применении алгоритма к этим данным
- 4. Совокупность тех элементов множества X, у которых есть соответствующие элементы в Y, называется областью определения функции,
- 5. Если область определения функции из X в Y совпадает с множеством X, то функция называется всюду
- 6. Функция у (x1, х2, ..., хn) называется вычислимой, если существует алгоритм, позволяющий вычислить ее значение по
- 7. Идея построения точного определения алгоритма, опирающегося на понятие вычислимой функции, состоит в том, что любые дискретные
- 8. Какие функции могут быть вычислимыми? Как описать такие алгоритмически вычислимые функции? Исследование этих вопросов привело к
- 9. 2. Построение вычислимой функции
- 10. В теории РФ принят конструктивный подход: все множество исследуемых объектов (функций) строится из некоторого базиса с
- 11. Все вычислимые функции можно построить на основе трех элементарных функций (базиса) путем применения к этим функциям
- 12. 2.1 Базисные функции
- 13. 1) Тождественное равенство нулю: On (x1, x2,…, xn)= 0 n-местная функция (функция от n аргументов), всегда
- 14. 2) Функция следования S1(x) = x+1 Одноместная функция, сопоставляющая любому натуральному числу x непосредственно следующее за
- 15. 3) Функция тождественного повтора одного из аргументов (функция проекции): n-местная функция, сопоставляющая любому упорядоченному набору натуральных
- 16. Пример1 Вычисление простейших функций
- 17. 2.2. Операторы
- 18. 1) Оператор суперпозиции (подстановки) Оператором суперпозиции называется подстановка в функцию от n переменных n функций от
- 19. Говорят, что функция h получена из функций g, f1,..., fn суперпозицией (или подстановкой). Обозначение: h =
- 20. Пример 2 Найти значение S(S1, O1) g(x) = S1, f (x)= O1 -> h(у) = g(f
- 21. Пример 3 Найти значение S (I22, I11 ,О1) В этом случае конечная функция будет двухместной следовательно
- 22. 2) Оператор примитивной рекурсии Оператор примитивной рекурсии определяет (n+1)-местную функцию f через n-местную функцию g и
- 23. Независимо от числа переменных в f рекурсия ведется только по одной переменной у. Остальные n переменных
- 24. Если умеем находить значения функций g и h, то значения функции f(x1,..., xn, у + 1)
- 25. Пример 4. Пусть g(x) = x – функция от 1 переменной (n=1), h - функция от
- 26. f (x, 0) = g(x) = x f (x, 1) = h (x, 0, f(x,0)) =
- 27. Если нужно доказать примитивную рекурсивность некоторой функции, нужно ее представить через простейшие функции и/или через функции
- 28. Пусть заданы два множества X и Y. Если некоторым элементам X поставлены в соответствие однозначно определенные
- 29. Частичная функция f (х1,х2,…,хn) называется примитивно рекурсивной, если ее можно получить конечным числом операций суперпозиции и
- 30. Пример 5. Покажем, что функция константа является примитивно-рекурсивной f(x) = m = S1(...(S1(O(x)))...) m раз
- 31. Пример 6. Покажем, что двухместная функция f(х,у) = х + у является примитивно-рекурсивной Так как функция
- 32. f сум (x,0) = g(x) = x, f сум (x, 1) = h(x,0, f (x,0)) =
- 33. Пример 7. Покажем, что двухместная функция f(х,у) = х*у является примитивно-рекурсивной Для этого мы должны показать,
- 34. Определим функции g и h При у=0 fумн(x, 0) = x*0= 0 = g(x) = O1(x)
- 35. fумн(x,0) = g(x) = 0, fумн(x,1) = h(x,0, fумн(x,0)) = x+ fумн(x,0) = x +0=x fумн(x,2)
- 36. Функция f(x,y)=х*у образуется из простейшей функции тождественного равенства нулю и примитивно-рекурсивной функции сложения операцией примитивной рекурсии
- 37. Так как функция f является функцией 2х аргументов, то для использования операции примитивной рекурсии мы должны
- 38. При у=0 fст(x, 0) = x^0= 1 = g(x) =S1(O1(x)) - суперпозиция нуль-функции и функции следования
- 39. f ст (x,0) = g(x) = 1, f ст (x,1) = h(x,0, f ст(x,0)) =х* f
- 40. Функция f(x,y)=х^у образуется из суперпозиции простейших функции тождественного равенства нулю, следования и примитивно-рекурсивной функции умножения операцией
- 43. Таким образом, из простейших функций с помощью операторов суперпозиции и примитивной рекурсии можно получить множество функций,
- 44. Однако, не все вычислимые функции можно описать как примитивно-рекурсивные (пример ф-я Аккермана) т. е. понятие примитивно-рекурсивная
- 45. Функция f(х1,х2,…,хn) называется частично рекурсивной, если ее можно получить с помощью конечного числа операторов суперпозиции, примитивной
- 46. 3) μ-оператор (оператор минимизации для функции n аргументов) Пусть задана функция f(х1,х2,…,хn-1, y). Зафиксируем значения х1,х2,…,хn-1,
- 47. Оператор минимизации “следит”, при каком значении выбранного аргумента наблюдаемая им функция впервые опустится до нуля. Это
- 48. Работа μ-оператора Рассмотрим F(х1,х2,…,хn-1) = μy[f(х1,х2,…,хn-1,y) = 0], где y - выделенная переменная. Работу μ-оператора можно
- 49. Для вычисления функции F: Вычисляем f(х1,х2,…,хn,0); если значение равно нулю, то полагаем F (х1,х2,…,хn) = 0.
- 50. Пример 8. работа μ-оператора Пусть функция g(х, y) = х - у + 3. Зафиксируем х
- 51. Доказано, что: множество частично-рекурсивных функций совпадает с множеством вычислимых функций - алгоритмически разрешимых задач.
- 52. Рассмотрим как выполняются основные требования к алгоритмам для алгоритмической модели „частично-рекурсивные функции“
- 53. Детерминированность определяется полной определенностью в вычислении базисных функций и полной заданностью в действиях операторов. Там же
- 54. Результатом является значение частично-рекурсивной функции, вычисляемой в процессе применения операторов Возможность выбора в качестве аргумента любого
- 55. Таким образом, понятие ЧРФ является исчерпывающей формализацией понятия алгоритма. Это выражено в виде тезиса Чёрча: всякий
- 56. Вопросы к лекции 1. Как понятие алгоритма связано с понятием вычислимой функции? 2. Перечислите простейшие функции
- 57. Семинар
- 58. Задание 1. Применение оператора суперпозиции Даны 3 функции от двух переменных: f1(x1, x2) = 2 x1+3x2
- 59. Задание 2 (самостоятельно) Даны три одноместные функции: f1(x) = O1(x) f2(x) = O1(x) f3(x) = S1(10)
- 60. Задание 3 Применение оператора примитивной рекурсии Пусть g(x) = 0 – функция от 1 переменной h(x,y,z)
- 61. Задание 4 (самостоятельно) Пусть g(x1,x2) = x1*x2 – функция от 2 аргументов h(x1,x2,x3,x4) = x1*x2+x3*x4 –
- 63. Скачать презентацию

































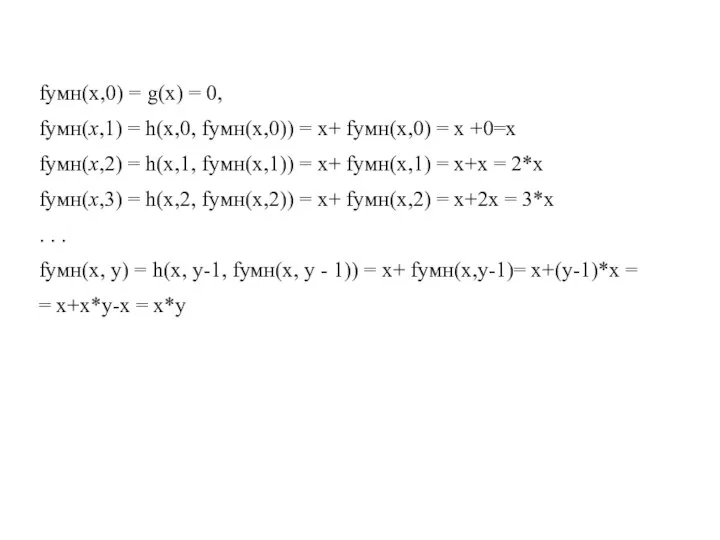



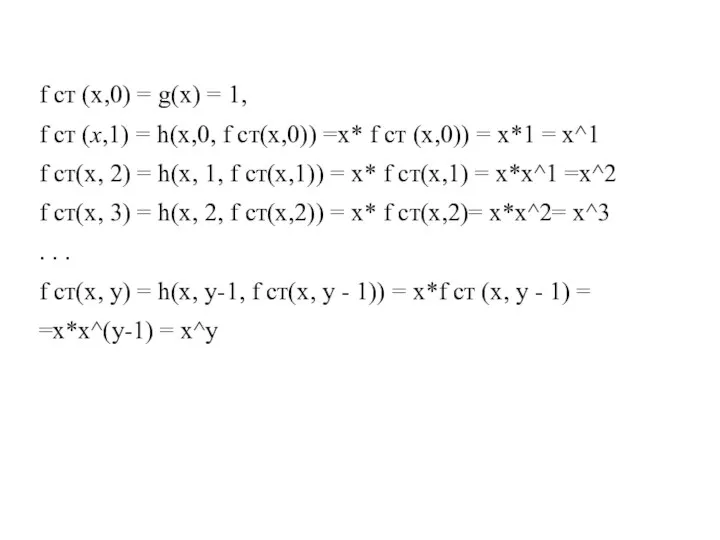

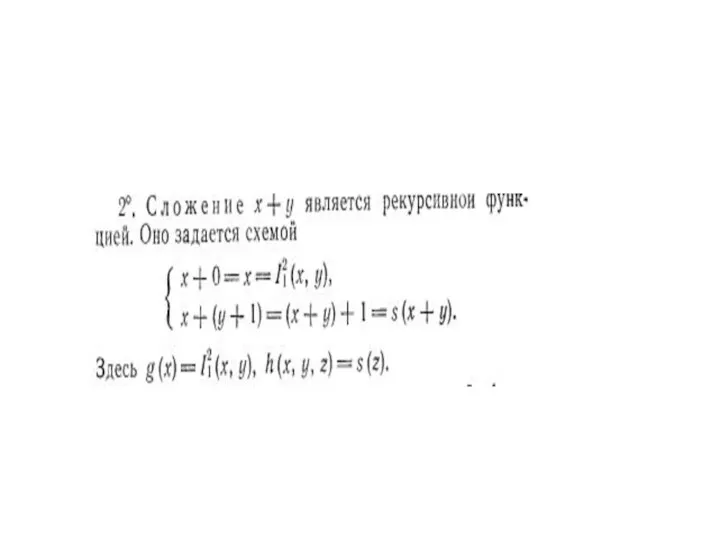






![Работа μ-оператора Рассмотрим F(х1,х2,…,хn-1) = μy[f(х1,х2,…,хn-1,y) = 0], где y -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1458402/slide-47.jpg)













 Метод координат на плоскости
Метод координат на плоскости Аттестационная работа. Методическая разработка рабочей программы элективного курса. (9 класс)
Аттестационная работа. Методическая разработка рабочей программы элективного курса. (9 класс) Презентация на тему Прямая линия Кривая линия
Презентация на тему Прямая линия Кривая линия  Интегрированный урок: математика + биология. Простые и сложные листья
Интегрированный урок: математика + биология. Простые и сложные листья Прибавление 5, 6, 7
Прибавление 5, 6, 7 Уравнения и неравенства. 11 класс
Уравнения и неравенства. 11 класс Іштей және сырттай сызылған төртбұрыштар
Іштей және сырттай сызылған төртбұрыштар Задачи на движение. Математические модели
Задачи на движение. Математические модели Углы и отрезки, связанные с окружностью. 10 класс
Углы и отрезки, связанные с окружностью. 10 класс Сравнение чисел. 6 класс
Сравнение чисел. 6 класс Тригонометрические уравнения
Тригонометрические уравнения  Урок математики в 1 классе
Урок математики в 1 классе Презентация по математике "Сложение и вычитание отрезков" - скачать бесплатно
Презентация по математике "Сложение и вычитание отрезков" - скачать бесплатно Лекция 9. Методи розв’язання систем лінійних алгебраїчних рівнянь (СЛАР)
Лекция 9. Методи розв’язання систем лінійних алгебраїчних рівнянь (СЛАР) Аттестационная работа. Образовательная программа внеурочной деятельности «Математический калейдоскоп»
Аттестационная работа. Образовательная программа внеурочной деятельности «Математический калейдоскоп» Корреляционный анализ
Корреляционный анализ Луч. Дополнительные лучи. 5 класс
Луч. Дополнительные лучи. 5 класс Математика в архитектуре
Математика в архитектуре Центр начального образования. Формирование и мониторинг умений младших школьников по разделу «Работа с текстовой задачей»
Центр начального образования. Формирование и мониторинг умений младших школьников по разделу «Работа с текстовой задачей» Матрицы и действия на ними
Матрицы и действия на ними Презентация по математике Корень n-ой степени
Презентация по математике Корень n-ой степени  Теорема о трех перпендикулярах, ее применение при решении задач
Теорема о трех перпендикулярах, ее применение при решении задач Степенные функции, их свойства и графики (11 класс)
Степенные функции, их свойства и графики (11 класс) Использовать на уроке повторения темы «Логарифмы»
Использовать на уроке повторения темы «Логарифмы» Вправи на засвоєння таблиці додавання і віднімання числа 7
Вправи на засвоєння таблиці додавання і віднімання числа 7 Простейшие вероятностные задачи
Простейшие вероятностные задачи Презентация по математике "Шкалы и координаты" - скачать бесплатно
Презентация по математике "Шкалы и координаты" - скачать бесплатно Что такое задача
Что такое задача