Содержание
- 2. Цели урока: Обучающие: обобщение и систематизация знаний по теме; ликвидация пробелов в знаниях учащихся; установление внутри
- 3. Наша цель: обобщить опыт решения квадратных уравнений, научиться выбирать рациональный путь решения.
- 4. Уравнение вида , где х- переменная, a,b,c – числа , причем называется квадратным.
- 5. Коэффициенты уравнения: а – первый (или старший ) коэффициент, в – второй коэффициент, с – третий
- 6. История развития квадратных уравнений Квадратные уравнения в Багдаде (9 век) Квадратные уравнения в Древнем Вавилоне Квадратные
- 7. Квадратные уравнения в Багдаде(9 век): Впервые квадратные уравнения появились в городе Багдаде, их вывел приглашённый математик
- 8. Квадратные уравнения в Древнем Вавилоне: Необходимость решать уравнения не только первой, но и второй степени ещё
- 9. Квадратные уравнения в Европе в 13 - 17 веках: Формулы решения квадратных уравнений в Европе были
- 10. 1. Если b=0 и c=0, то… уравнение примет вид ax²=0 Например: 5x²=0 x²=0 x1,2=0 Тогда ax²=0
- 11. 2. Если b=0, a c≠0, то… ax²+c=0, x²= -c/a Если –с/a>0, Если –c/a 3x²= -2 x²=
- 12. 3. Если b≠0, а c=0, то… Уравнение примет вид ax²+bx=0 Тогда: x(ax+b)=0 x=0, или ax+b=0 x1=0;
- 13. ax2 + bx + c = 0 D = b2 – 4ac D≻0 D=0 D≺0 х
- 14. Теорема Виета Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение
- 15. Пригласительный билет
- 16. Пригласительный билет
- 17. 1. Метод выделения квадрата двучлена Цель: привести уравнение общего вида к неполному квадратному уравнению. В этом
- 18. Самостоятельно решить методом выделения квадрата двучлена x2 - 6x + 8 = 0
- 19. 2. Метод: если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй, по
- 20. Самостоятельно решить методом 2 157x2 + 20x - 177 = 0
- 21. 3. Метод: если в квадратном уравнении a+c=b, то один из корней равен 1, а второй, по
- 22. Самостоятельно решить методом 3 203x2 + 220x + 17 = 0
- 23. 4. Метод введения новой переменной (5x+3)2 = 3(5x+3) – 2
- 24. Подведение итогов: Итак, подведем итог. Решение квадратных уравнений возможно осуществлять разными методами. Для квадратных уравнений применимы
- 25. Домашнее задание: Решите уравнение x2 + 6x -16= 0 методом выделения квадрата двучлена. Решите уравнение(x2–x)2-14(x2–x)+24 =
- 27. Скачать презентацию
























 Прямоугольный параллелепипед
Прямоугольный параллелепипед Урок математики в 1 классе. Уменьшаемое. Вычитаемое. Разность
Урок математики в 1 классе. Уменьшаемое. Вычитаемое. Разность Регрессионный анализ
Регрессионный анализ Многоугольники
Многоугольники Дан параллелепипед АВСA1B1C1D1. Назовите вектор
Дан параллелепипед АВСA1B1C1D1. Назовите вектор Положительные и отрицательные числа. Координатная прямая
Положительные и отрицательные числа. Координатная прямая Цилиндр. Площадь поверхности. 11 класс
Цилиндр. Площадь поверхности. 11 класс Задачи на проценты
Задачи на проценты Урок по математике в 5 классе. Урок по математике в 5 классе. Тема: «Сложение и вычитание десятичных дробей
Урок по математике в 5 классе. Урок по математике в 5 классе. Тема: «Сложение и вычитание десятичных дробей Решение задач с помощью уравнений
Решение задач с помощью уравнений Площади фигур
Площади фигур Функции. Определение функции
Функции. Определение функции Степень с натуральным показателем. Ребусы
Степень с натуральным показателем. Ребусы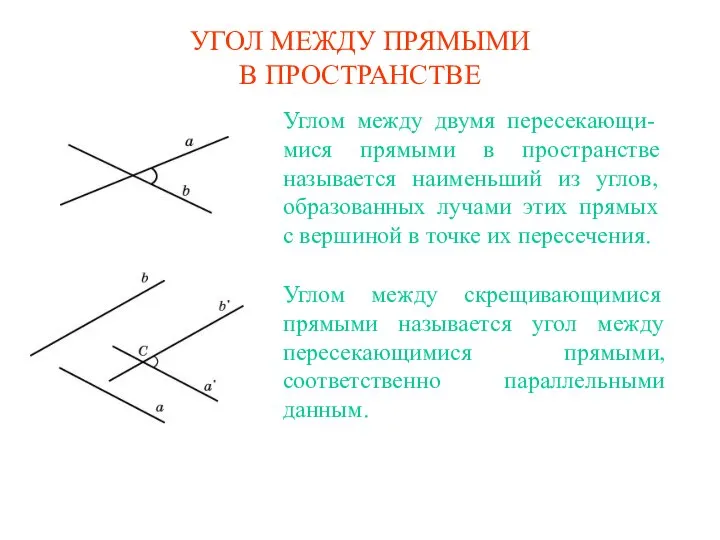 Угол между прямыми в пространстве
Угол между прямыми в пространстве Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Алгоритм решения линейных уравнений
Алгоритм решения линейных уравнений «ДАВАЙТЕ ПОЗНАКОМИМСЯ» КЛАССНЫЙ ЧАС
«ДАВАЙТЕ ПОЗНАКОМИМСЯ» КЛАССНЫЙ ЧАС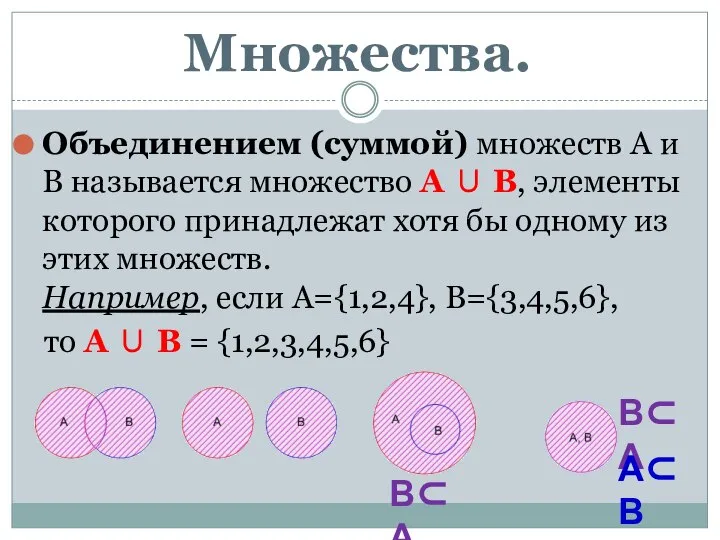 Множества. Комбинаторика
Множества. Комбинаторика Памятка по оформлению краткой записи к задачам
Памятка по оформлению краткой записи к задачам Простейшие задачи в координатах
Простейшие задачи в координатах Презентация по математике "Задачи на прямоугольник" - скачать бесплатно
Презентация по математике "Задачи на прямоугольник" - скачать бесплатно Взаимно обратные числа. 6 класс
Взаимно обратные числа. 6 класс Первообразная и интеграл
Первообразная и интеграл Десятичные и натуральные логарифмы. Формула перехода к новому основанию
Десятичные и натуральные логарифмы. Формула перехода к новому основанию Формирование познавательных учебных действий на уроках математики
Формирование познавательных учебных действий на уроках математики Вычисления и преобразования
Вычисления и преобразования Формулы сокращенного умножения
Формулы сокращенного умножения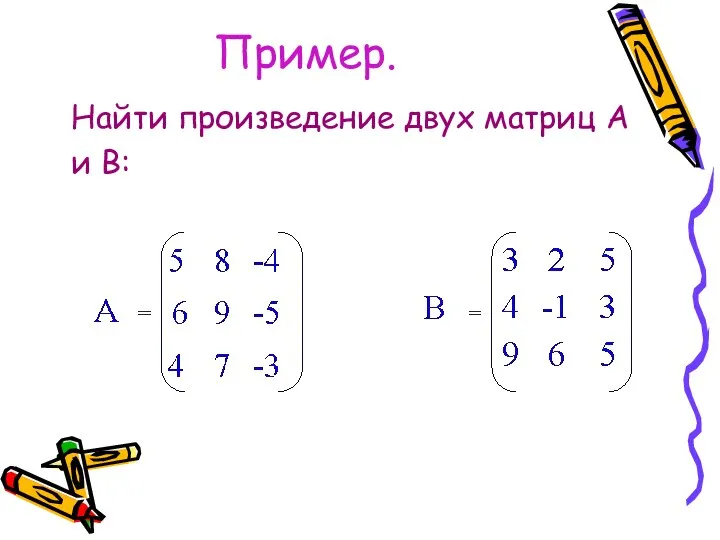 Умножение матриц
Умножение матриц