Содержание
- 2. Классификация дифференциальных уравнений обыкновенные дифференциальные уравнения, содержащие одну независимую переменную и производные по ней; дифференциальные уравнения
- 3. Примеры дифференциальных уравнений уравнение свободных колебаний уравнение вынужденных колебаний уравнение Лапласа одномерное волновое уравнение уравнение теплопроводности
- 4. Типы задач задача Коши краевая задача Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной
- 5. Решение ОДУ в MathCAD Given :=Odesolve( , ,[ ])
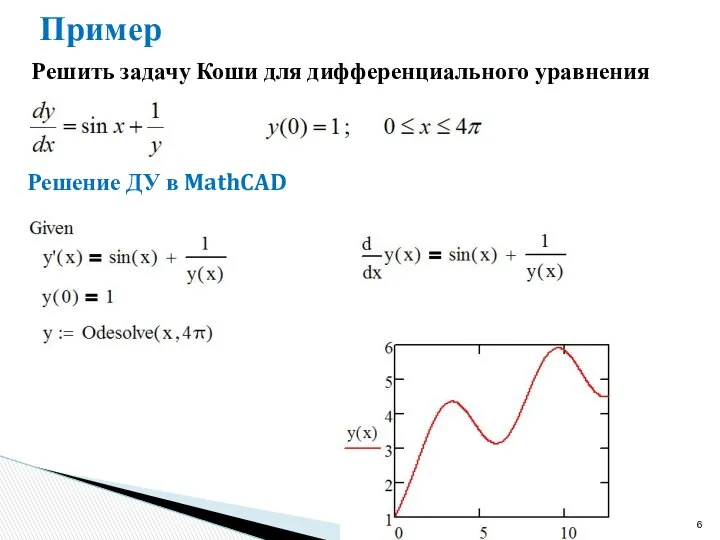
- 6. Пример Решить задачу Коши для дифференциального уравнения Решение ДУ в MathCAD
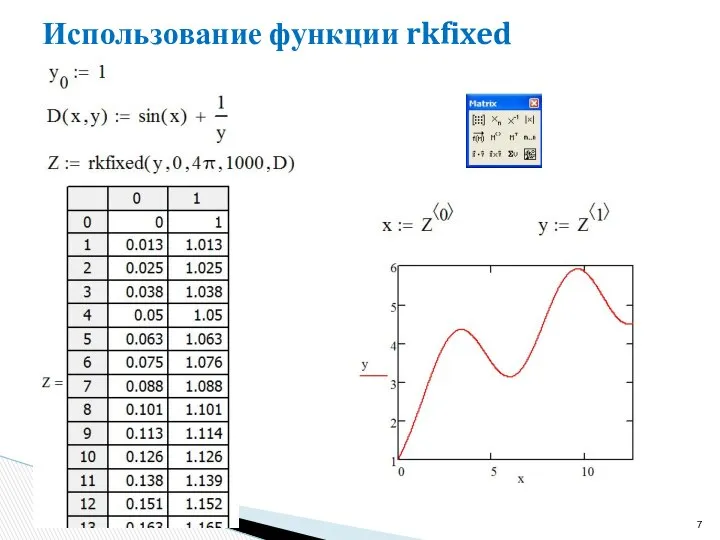
- 7. Использование функции rkfixed
- 8. Численные методы решения задачи Коши Две группы методов: одношаговые методы; методы прогноза и коррекции (многошаговые методы).
- 9. Численные методы решения задачи Коши Одношаговые методы: метод Эйлера; модифицированный метод Эйлера; метод Рунге-Кутты. Методы прогноза
- 10. Погрешности Источники погрешностей: погрешность округления; погрешность усечения; погрешность распространения. Погрешность распространения – результат накопления погрешностей, появившихся
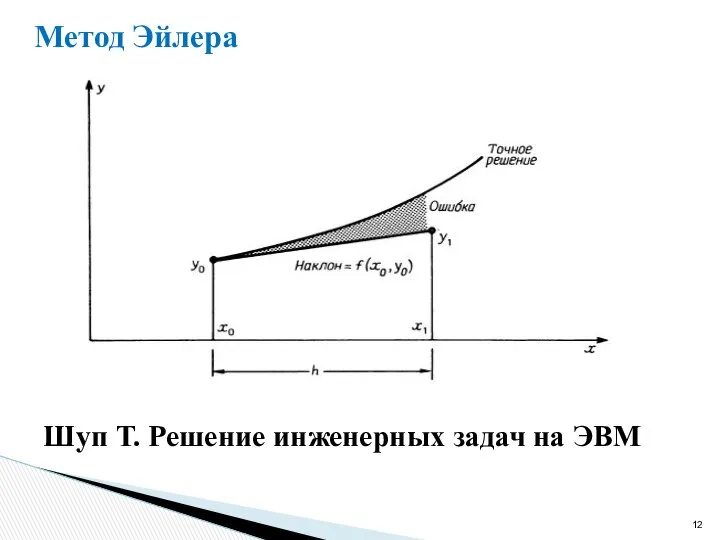
- 11. Метод Эйлера Формула Эйлера рекуррентное соотношение
- 12. Шуп Т. Решение инженерных задач на ЭВМ Метод Эйлера
- 13. Программирование метода Эйлера double f(double x, double y) { return 2*x*x + 2*y; }
- 14. Программирование метода Эйлера void rdy_Eiler(double *x, double *y, double b, int n) { int i; double
- 15. Программирование метода Эйлера void __fastcall TForm1::Button1Click(TObject *Sender) { double *x, *y; int i, n = 10;
- 16. Модифицированный метод Эйлера Ошибка
- 17. Модифицированный метод Эйлера void rdy_MEiler(double *x, double *y, double b, int n) { int i; double
- 18. Метод Рунге-Кутты Ошибка
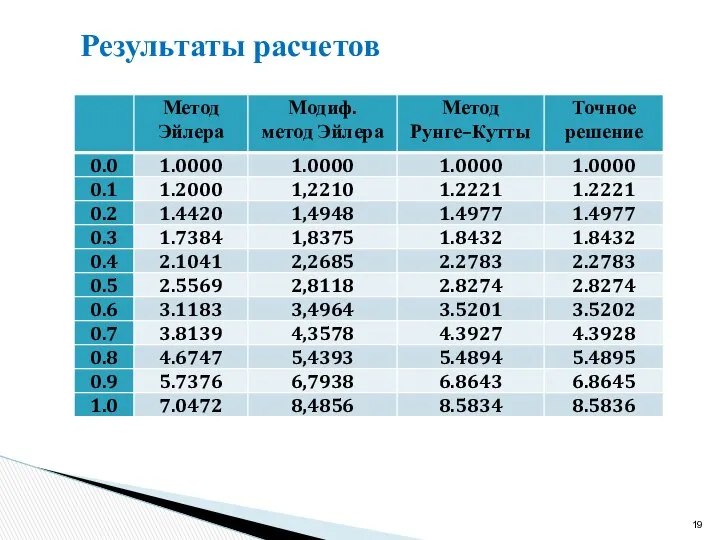
- 19. Результаты расчетов
- 20. Общая характеристика одношаговых методов чтобы получить информацию в новой точке, надо иметь данные лишь в одной
- 21. Методы прогноза и коррекции Для этого применяются две формулы: формула прогноза; формула коррекции. В этих методах
- 22. Метод Милна Этап прогноза (формула Милна): Этап коррекции (формула Симпсона): Методы прогноза и коррекции не обладают
- 23. Метод Милна void rdy_Miln(double *x, double *y, double b, int n) { int i; double h
- 24. Метод Милна while (1) { y1 = y[i-1] + h/3*(dy1 + 4*dy[i] + dy[i-1]); dy2 =
- 25. Методы Рунге–Кутты для системы дифференциальных уравнений Начальные условия
- 26. Методы Рунге–Кутты для системы дифференциальных уравнений
- 27. Методы Рунге–Кутты для системы дифференциальных уравнений
- 28. Методы Рунге–Кутты для системы дифференциальных уравнений
- 29. Задание Написать программу решения обыкновенного дифференциального уравнения с использованием метода Эйлера (Delphi) с построением графика. Написать
- 31. Скачать презентацию



![Решение ОДУ в MathCAD Given :=Odesolve( , ,[ ])](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463716/slide-4.jpg)














![Метод Милна while (1) { y1 = y[i-1] + h/3*(dy1 +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1463716/slide-23.jpg)





 Натуральные и целые числа
Натуральные и целые числа Элементы комбинаторики
Элементы комбинаторики Шах и Мат. Курс ЭМШ по математике 2017-1018
Шах и Мат. Курс ЭМШ по математике 2017-1018 Урок математики в 4 классе Закрепление изученного материала по теме: «Скорость, время, расстояние». Автор: учител
Урок математики в 4 классе Закрепление изученного материала по теме: «Скорость, время, расстояние». Автор: учител Пересекающиеся и параллельные прямые
Пересекающиеся и параллельные прямые Презентация по математике "Процентные расчеты на каждый день" - скачать
Презентация по математике "Процентные расчеты на каждый день" - скачать  Стандартный вид многочлена
Стандартный вид многочлена Паралельне проектування та його властивості
Паралельне проектування та його властивості Выражения и их преобразования. Упражнение 1
Выражения и их преобразования. Упражнение 1 Учимся писать цифры от 0 до 9
Учимся писать цифры от 0 до 9 Правильные многоугольники. Платоновы тела
Правильные многоугольники. Платоновы тела Признаки параллельности двух прямых
Признаки параллельности двух прямых Алгебра. Графики функций
Алгебра. Графики функций Уравнение прямой на плоскости
Уравнение прямой на плоскости Первообразная Интеграл
Первообразная Интеграл Математика вокруг нас
Математика вокруг нас Способ приведения матрицы к ступенчатому виду
Способ приведения матрицы к ступенчатому виду Архимед в XXI веке
Архимед в XXI веке Презентация на тему Округление чисел.
Презентация на тему Округление чисел. Что нам стоит дом построить?
Что нам стоит дом построить? Экстремумы функции
Экстремумы функции Интеграл, интеграция, интегрирование. Решение задач
Интеграл, интеграция, интегрирование. Решение задач Умножение десятичных дробей
Умножение десятичных дробей Приближенное решение уравнений
Приближенное решение уравнений Четырехугольники
Четырехугольники Математическая викторина: «Учиться не легко, но интересно» Составила: учитель математики Щемелева Нина Валерьевна МОУ СОШ №18
Математическая викторина: «Учиться не легко, но интересно» Составила: учитель математики Щемелева Нина Валерьевна МОУ СОШ №18  Тест 2 по математике
Тест 2 по математике Порахуй з Вовком! Автор Рудакова Л.В., учитель початкових класів Новотроїцької ЗШ І- ІІІ ст. № 4 Волноваського району Донецької об
Порахуй з Вовком! Автор Рудакова Л.В., учитель початкових класів Новотроїцької ЗШ І- ІІІ ст. № 4 Волноваського району Донецької об