Содержание
- 2. Независимые повторные испытания. Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит
- 3. Независимые повторные испытания. Примеры: Подбрасываем игральный кубик n раз. Выпадение числа очков от 1 до 6
- 4. Независимые повторные испытания. Независимые повторные испытания, в каждом из которых возможно появление события А (успех) с
- 5. Формула Бернулли. Пусть производится n испытаний Бернулли. Вероятность того, что в этих испытаниях событие А произойдет
- 6. Формула Бернулли. Решение. Обозначим А- расход не превысит норму. По условию n = 7, m =
- 7. Формула Бернулли Пример. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть одному из них 2
- 8. Формула Бернулли Пример. Исследование инкубации яиц яичного кросса Беларусь-9 показало, что цыплята выводятся в среднем из
- 9. Наивероятнейшее число появлений события. Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности
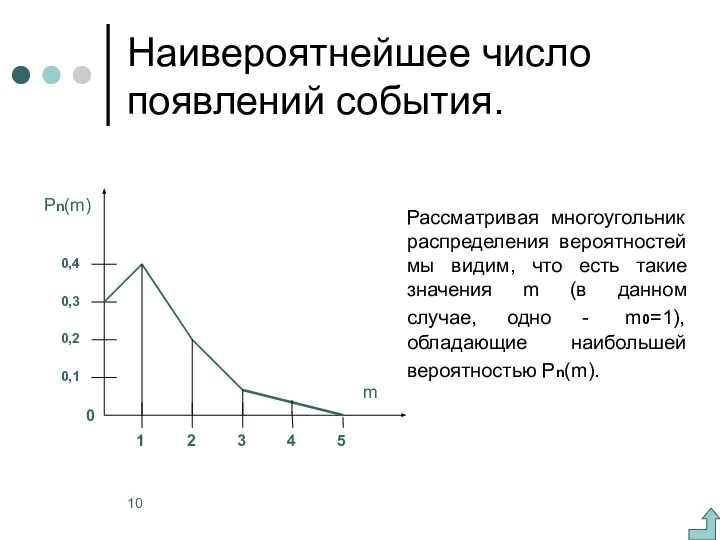
- 10. Наивероятнейшее число появлений события. Рассматривая многоугольник распределения вероятностей мы видим, что есть такие значения m (в
- 11. Наивероятнейшее число появлений события. Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если
- 12. Наивероятнейшее число появлений события. Пример. В результате многолетних наблюдений вероятность дождя 21 июля в городе N
- 13. Приближённые формулы в схеме Бернулли. Локальная теорема Лапласа.
- 14. Пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над
- 15. Приближённые формулы 1. Локальная формула Муавра-Лапласа (n>10, p>0,1). 2. Формула Пуассона (n>10, p 3. Интегральная формула
- 16. Локальная формула Муавра- Лапласа (n∙p∙q ≥ 10). . Если вероятность р появления события А в каждом
- 17. Пользуясь этой таблицей, необходимо иметь в виду свойства функции : 1. Функция является четной, т.е. .
- 18. npq = 400 ∙ 0,8∙ (1—0,8) = 64 > 10; . По таблице найдем Пример. В
- 19. Формула Пуассона (λ ≤ 10). Теорема. Если вероятность p наступления события А в каждом испытании постоянно
- 20. Существуют статистико-математические таблицы для распределения Пуассона.
- 21. Пример. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно
- 22. Интегральная теорема Лапласа (n∙p >10) Интегральная теорема Муавра—Лапласа. Если вероятность р наступления события А в каждом
- 23. Функция Ф(х) называется функцией Лапласа. Свойства функции Ф(х): Функция Ф(х) нечетная, т.е. Ф(-х) = - Ф(х).
- 24. Пример. В некоторой местности из каждых 100 семей 80 имеют холодильники. Необходимо найти вероятность того, что
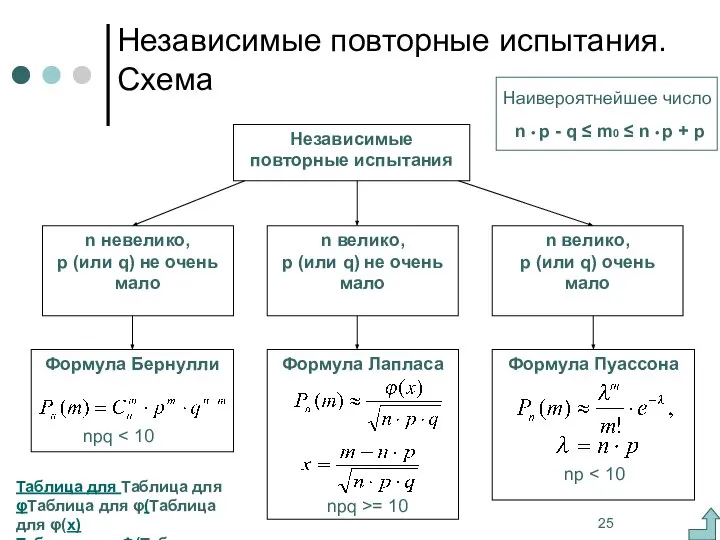
- 25. Независимые повторные испытания. Схема Таблица для Таблица для φТаблица для φ(Таблица для φ(x) Таблица для Ф(Таблица
- 27. Скачать презентацию






















 Пропорція. Основна властивість пропорції
Пропорція. Основна властивість пропорції Прикладная математика. Системы уравнений
Прикладная математика. Системы уравнений Решение уравнений. Устный счет
Решение уравнений. Устный счет Найдите значение выражения. ЕГЭ-2014 В-11
Найдите значение выражения. ЕГЭ-2014 В-11 Квадратный трехчлен. Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлен
Квадратный трехчлен. Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлен Параллельные плоскости
Параллельные плоскости Учение – это сила. Зимняя математическая олимпиада
Учение – это сила. Зимняя математическая олимпиада Единицы измерения длины
Единицы измерения длины Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве
Плоскость, как поверхность первого порядка. Уравнения плоскости и их исследование. Прямая в пространстве Интеграция математики и информатики
Интеграция математики и информатики Алгебра. 9 класс
Алгебра. 9 класс Тестовые задания. 7 класс. Геометрия
Тестовые задания. 7 класс. Геометрия Своя игра. Числа. Геометрия Ученые математики
Своя игра. Числа. Геометрия Ученые математики Моделирование процессов и объектов в производственных системах
Моделирование процессов и объектов в производственных системах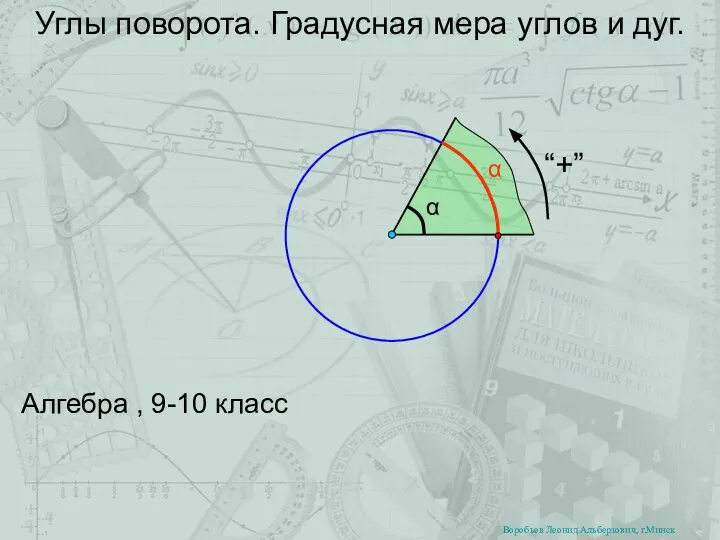 Углы поворота. Градусная мера углов и дуг
Углы поворота. Градусная мера углов и дуг Отношения и соотвествия
Отношения и соотвествия Действия с десятичными дробями. Задания
Действия с десятичными дробями. Задания Сложение чисел с разными знаками с помощью координатной прямой
Сложение чисел с разными знаками с помощью координатной прямой Арксинус и арккосинус
Арксинус и арккосинус Применение свойств квадратичной функции при решении уравнений с параметром
Применение свойств квадратичной функции при решении уравнений с параметром Теоремы сложения и умножения вероятностей
Теоремы сложения и умножения вероятностей Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г. Москвы
Автор: Макарова Татьяна Павловна, учитель математики высшей категории ГБОУ СОШ №618 г. Москвы  Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год
Составление переводной работы по алгебре в формате ЕГЭ, 2017-2018 учебный год Устный счет. Решаем в классе
Устный счет. Решаем в классе Соотношения между сторонами и углами прямоугольного треугольника
Соотношения между сторонами и углами прямоугольного треугольника Решение уравнений
Решение уравнений Нахождение дроби от числа
Нахождение дроби от числа Древні математики
Древні математики