Содержание
- 2. Системой m линейных уравнений с n неизвестными х1, х2, …, хn называется система вида aij -
- 3. Решением системы (*) называется такой набор чисел (с1, с2,…, сn), что при его подстановке в систему
- 4. Система называется определенной, если она имеет единственное решение; и неопределенной, если она имеет более одного решения.
- 5. Если b1=b2=…=bm=0, то система называется однородной; в противном случае она называется неоднородной. Две системы называются эквивалентными
- 6. Элементарными преобразованиями линейной системы называются следующие преобразования: - перестановка уравнений системы; - умножение или деление коэффициентов
- 7. Систему (*) можно записать в матричной форме: АХ=В, где матрица коэффициентов системы; матрица-столбец (вектор-столбец) неизвестных матрица-столбец
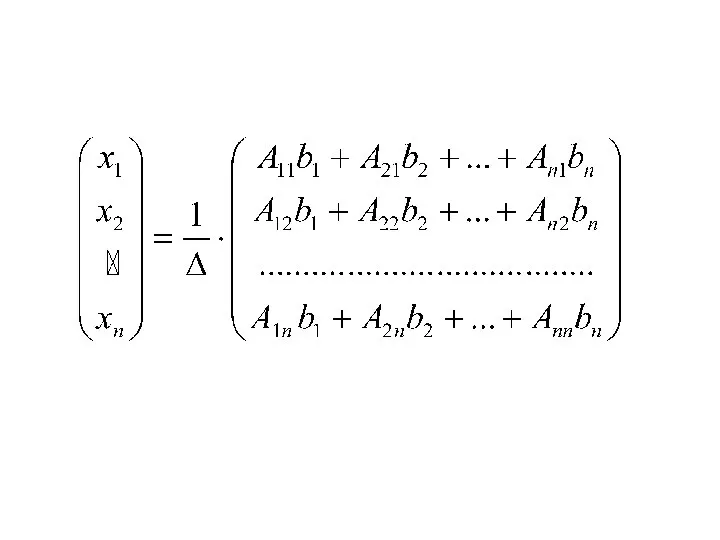
- 8. 1. Решение систем линейных уравнений при помощи обратной матрицы. матрица-столбец (вектор-столбец) неизвестных матрица-столбец (вектор-столбец) свободных членов
- 9. Пусть detA≠0, тогда ∃ А-1
- 10. Решить систему линейных уравнений при помощи обратной матрицы: А В
- 14. Ответ: (-2; 1; 2) то есть:
- 15. 2. Решение систем линейных уравнений по формулам Крамера. Система n уравнений с n неизвестными, определитель которой
- 16. Дана система n линейных уравнений с n неизвестными х1, х2, …, хn:
- 17. Систему можно записать в матричной форме: АХ=В, где матрица коэффициентов системы; матрица-столбец (вектор-столбец) неизвестных матрица-столбец (вектор-столбец)
- 18. пусть
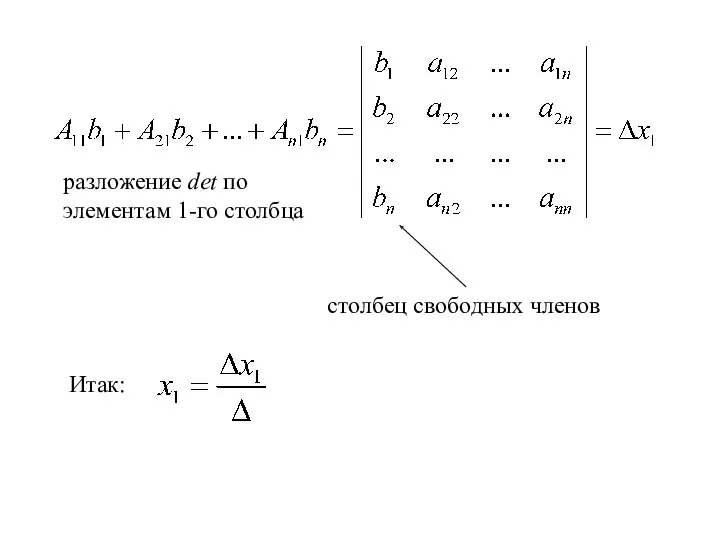
- 21. разложение det по элементам 1-го столбца Итак: столбец свободных членов
- 22. разложение det по элементам 2-го столбца Итак: столбец свободных членов
- 23. разложение det по элементам n-го столбца Итак: столбец свободных членов То есть:
- 24. Формулы Крамера где Δ=detA≠0, Δхk- определитель, получающийся из detA заменой к-го столбца на столбец свободных членов.
- 25. Решить систему линейных уравнений по формулам Крамера:
- 28. Скачать презентацию









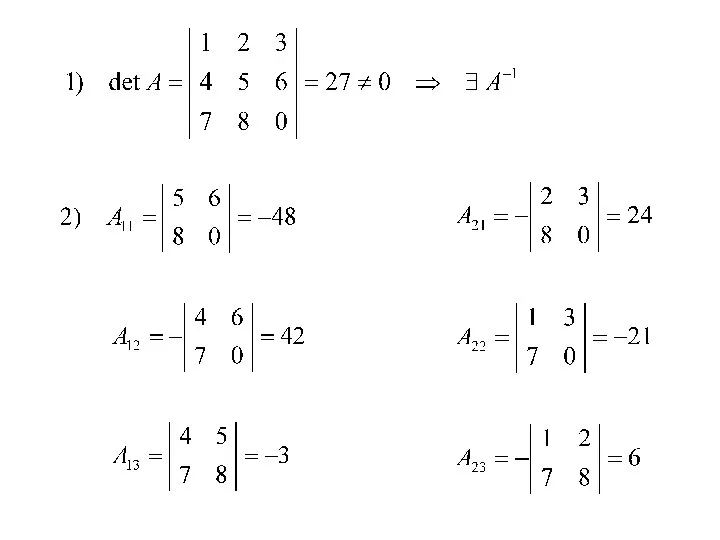
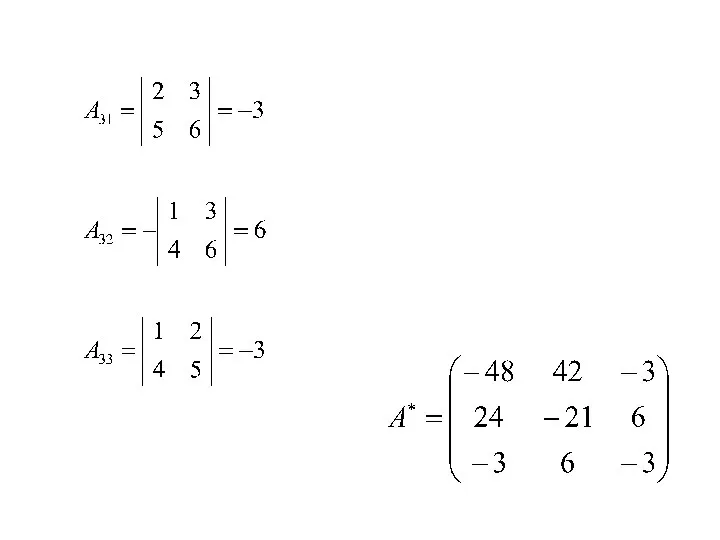
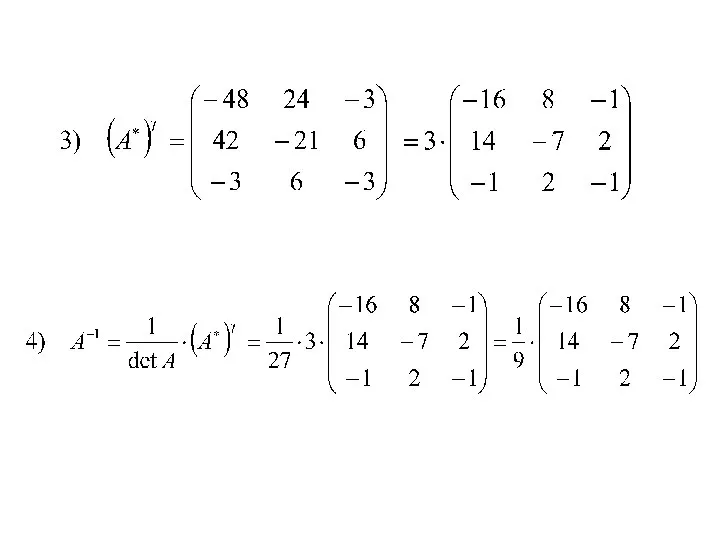











 N-ary relations and their applications. (Rosen 8.2)
N-ary relations and their applications. (Rosen 8.2) Необычные способы вычислений
Необычные способы вычислений Итоговый тест по алгебре для 7 класса
Итоговый тест по алгебре для 7 класса Центральная и осевая симметрия
Центральная и осевая симметрия Стереометрия. Поурочное планирование (10 -11 класс)
Стереометрия. Поурочное планирование (10 -11 класс) Презентация выполнена для первых уроков по теме «Обыкновенные дроби»
Презентация выполнена для первых уроков по теме «Обыкновенные дроби»  Элементы математической статистики
Элементы математической статистики Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие « Как выполняли арифметические действия в Древнем Риме?» составила: ученица 5 класса Вязова Луиза.
« Как выполняли арифметические действия в Древнем Риме?» составила: ученица 5 класса Вязова Луиза.  Вопросы по математике. Что? Где? Когда?
Вопросы по математике. Что? Где? Когда? Презентация по математике "Длина окружности" - скачать бесплатно
Презентация по математике "Длина окружности" - скачать бесплатно Движение
Движение Дорожная математика. Правила дорожного движения
Дорожная математика. Правила дорожного движения Презентация по математике "Тела вращения на примере конуса" - скачать
Презентация по математике "Тела вращения на примере конуса" - скачать  УРОК МАТЕМАТИКИ В 5 КЛАССЕ. ИЗМЕРЕНИЕ УГЛОВ. ТРАНСПОРТИР. Учитель математики МОУ СОШ
УРОК МАТЕМАТИКИ В 5 КЛАССЕ. ИЗМЕРЕНИЕ УГЛОВ. ТРАНСПОРТИР. Учитель математики МОУ СОШ  Теория вероятностей и математическая статистика
Теория вероятностей и математическая статистика Интересные факты о математике
Интересные факты о математике Trigonometriýa
Trigonometriýa Найдите площадь ABCD
Найдите площадь ABCD Занимательная математика
Занимательная математика Круговые и столбчатые диаграммы. Путешествие в мир продуктов питания
Круговые и столбчатые диаграммы. Путешествие в мир продуктов питания Теорема синусов
Теорема синусов Симметрия в пространстве
Симметрия в пространстве Sequential games. (Lecture 4)
Sequential games. (Lecture 4) Понятие вектора в пространстве
Понятие вектора в пространстве Презентация по математике "Решение задач на встречное движение" - скачать
Презентация по математике "Решение задач на встречное движение" - скачать  Презентация на тему Решение уравнений Математика, 5 класс
Презентация на тему Решение уравнений Математика, 5 класс Метод деления отрезка пополам
Метод деления отрезка пополам