Содержание
- 2. Найдём собственный вектор матрицы A. Т.к. E∙X = X, то матричное уравнение можно переписать в виде
- 3. Действительно, И следовательно,
- 4. Итак, получили систему однородных линейных уравнений для определения координат x1, x2, x3 вектора X. Чтобы система
- 5. Полученное уравнение 3-ей степени относительно λ называется характеристическим уравнением матрицы A и служит для определения собственных
- 6. Теорема Собственными числами матрицы А являются корни уравнения и только они.
- 7. Пример: Найти собственные векторы и соответствующие им собственные числа матрицы Решение: Составим характеристическое уравнение и найдём
- 8. 1. При λ1 = –1 получаем систему уравнений Если x1 = t, то, где t €
- 9. Найдем собственные вектора. Запишем матрицу Далее,
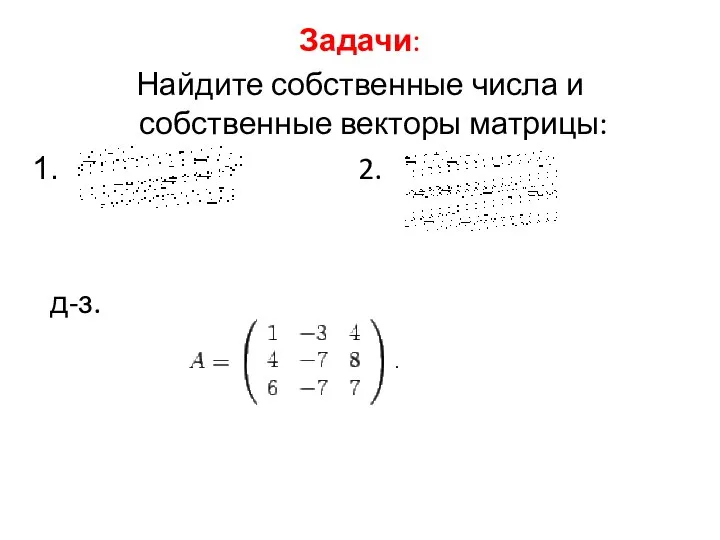
- 10. Задачи: Найдите собственные числа и собственные векторы матрицы: 2. д-з.
- 12. Скачать презентацию








 Занимательные задачи 5 класс Презентация Ученицы 5 Г класса Гимназии № 41 Галушкиной Юлии
Занимательные задачи 5 класс Презентация Ученицы 5 Г класса Гимназии № 41 Галушкиной Юлии  Сложение и вычитание векторов
Сложение и вычитание векторов Перпендикулярность прямой и плоскости (10 класс)
Перпендикулярность прямой и плоскости (10 класс) Производная и ее геометрический смысл. Урок обобщения и систематизации знаний
Производная и ее геометрический смысл. Урок обобщения и систематизации знаний Решение заданий №6 (трапеция) по материалам открытого банка задач ЕГЭ по математике 2016 года
Решение заданий №6 (трапеция) по материалам открытого банка задач ЕГЭ по математике 2016 года Метод алгебраического сложения. Алгебра 7 класс
Метод алгебраического сложения. Алгебра 7 класс Тест по теме «Окружность»
Тест по теме «Окружность» Из истории интересных чисел. Число П
Из истории интересных чисел. Число П Разложение чисел на простые множители
Разложение чисел на простые множители Основы теории погрешностей и математической статистики
Основы теории погрешностей и математической статистики Закрепление изученного материала. 1 класс
Закрепление изученного материала. 1 класс 20180311_matematika.izmerenie_uglov_5kl
20180311_matematika.izmerenie_uglov_5kl Правило вычисления значения алгебраической суммы двух чисел
Правило вычисления значения алгебраической суммы двух чисел Сравнение двух прогрессий
Сравнение двух прогрессий Геометрические характеристики поперечных сечений стержня
Геометрические характеристики поперечных сечений стержня Решение уравнений
Решение уравнений Могилатова Н.А. учитель математики МОУ СОШ №3, г.Балашов Муратова Т.В. учитель математики МОУ СОШ №3, г.Балашов Добрынина О.В. учит
Могилатова Н.А. учитель математики МОУ СОШ №3, г.Балашов Муратова Т.В. учитель математики МОУ СОШ №3, г.Балашов Добрынина О.В. учит Аттестационная работа. Загадки Красноярского края на уроках математики
Аттестационная работа. Загадки Красноярского края на уроках математики Решение квадратных уравнений по формуле. 8 класс
Решение квадратных уравнений по формуле. 8 класс Что такое математика?
Что такое математика? Решение задач
Решение задач Презентация по математике "Вычитание натуральных чисел" - скачать
Презентация по математике "Вычитание натуральных чисел" - скачать  Знакомство с умножением Зайнутдинова Г.Р. г. Оренбург
Знакомство с умножением Зайнутдинова Г.Р. г. Оренбург  Производная функции
Производная функции Ломаная. 5 класс
Ломаная. 5 класс Презентация по математике "Математика и русский язык: сотрудничество или конфликт?" - скачать
Презентация по математике "Математика и русский язык: сотрудничество или конфликт?" - скачать  Площадь трапеции Геометрия 8 класс, Л.С. Атанасян, Выполнила Сахарова М.А.
Площадь трапеции Геометрия 8 класс, Л.С. Атанасян, Выполнила Сахарова М.А.  Прогрессии в окружающей нас жизни
Прогрессии в окружающей нас жизни