Содержание
- 2. Решение алгебраических сравнений Пусть многочлены Будем рассматривать сравнения вида Такие сравнения называют алгебраическими Если в такое
- 3. Теорема 1 Если число с удовлетворяет сравнению то и весь класс по модулю т состоит из
- 4. Определение Решением сравнения называется класс чисел по модулю т, удовлетворяющих этому сравнению Числом решений сравнения называют
- 5. Примеры 1. Непосредственная проверка показывает, что в полной системе наименьших по абсолютной величине вычетов –5, –4,
- 6. Равносильные сравнения Определение Пусть Сравнения и называются равносильными (эквивалентными), если множества чисел, удовлетворяющих этим сравнениям, совпадают
- 7. Теорема 2 1) Если к обеим частям сравнения прибавим любой многочлен , то получим сравнение, равносильное
- 8. Теорема 3 Пусть и – многочлены с целыми коэффициентами. Если , , …, , то сравнения
- 9. Определение Степенью сравнения называют степень многочлена , если старший коэффициент не делится на т Пример Степень
- 10. Лекция 8 СРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ
- 11. Сравнения 1-ой степени Сравнение 1-ой степени может быть приведено к виду Теорема 4 Если , то
- 12. Методы решений сравнения Метод подбора Использование теоремы Эйлера Метод преобразования коэффициентов
- 13. Теорема 6 Если и b не делится на d, то сравнение (2) не имеет решений Теорема
- 14. Алгоритм решения сравнения Убедившись, что и , делим обе части и модуль сравнения (2) на d
- 15. Неопределённые уравнения Диофантово уравнение первой степени с двумя неизвестными , где Требуется решить это уравнение в
- 17. Скачать презентацию














 Парабола
Парабола Логарифмические уравнения и неравенства
Логарифмические уравнения и неравенства Математический анализ в шахматах
Математический анализ в шахматах Численные меоды. Вычислительная математика
Численные меоды. Вычислительная математика Исполнение линейного алгоритма. Подготовка к ГИА. (Задания В8)
Исполнение линейного алгоритма. Подготовка к ГИА. (Задания В8) Число и цифра 3
Число и цифра 3 Графики функций y=ax2+n ,у=a(x-m)2 , у=a(x-m)2 +n
Графики функций y=ax2+n ,у=a(x-m)2 , у=a(x-m)2 +n Деление десятичной дроби на десятичную дробь
Деление десятичной дроби на десятичную дробь Көп айнымалылар функциясы
Көп айнымалылар функциясы Круги Эйлера
Круги Эйлера Определители и их применения
Определители и их применения Программирование задач управления с использованием методов статистического анализа на языке R
Программирование задач управления с использованием методов статистического анализа на языке R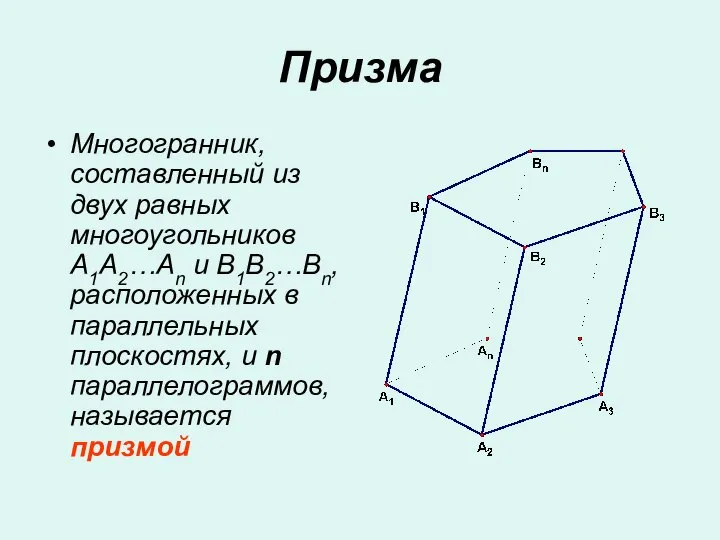 Призма как многогранник
Призма как многогранник Разнообразие математических закономерностей, используемых природой
Разнообразие математических закономерностей, используемых природой Формулы. Повторение
Формулы. Повторение Решение задач на применение первого признака равенства треугольников
Решение задач на применение первого признака равенства треугольников Золотое сечение в живой природе
Золотое сечение в живой природе Презентация по математике "Путешествие по Солнечной системе" - скачать бесплатно
Презентация по математике "Путешествие по Солнечной системе" - скачать бесплатно Введение в комбинаторику
Введение в комбинаторику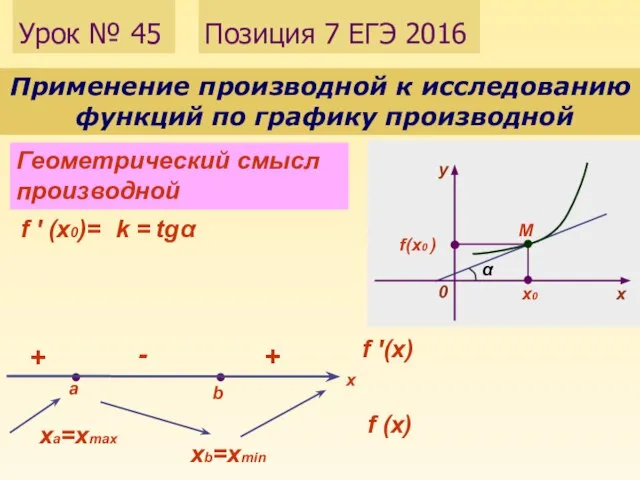 Позиция 7 ЕГЭ 2016. Применение производной к исследованию функций по графику производной. Геометрический смысл производной
Позиция 7 ЕГЭ 2016. Применение производной к исследованию функций по графику производной. Геометрический смысл производной Порядок построения правильной треугольной пирамиды
Порядок построения правильной треугольной пирамиды Algorytmy i struktury danych
Algorytmy i struktury danych Признаки равенства треугольников. Решение задач
Признаки равенства треугольников. Решение задач Нахождение части от числа и нахождение числа по его части Титова Н.Ю. 2012год. Презентация к уроку математики 5класс. Дифференциров
Нахождение части от числа и нахождение числа по его части Титова Н.Ю. 2012год. Презентация к уроку математики 5класс. Дифференциров Выбор проектных параметров отдельных объектов наземной космической инфраструктуры. Лекция № 22
Выбор проектных параметров отдельных объектов наземной космической инфраструктуры. Лекция № 22 Графический способ решения систем уравнений с двумя переменными
Графический способ решения систем уравнений с двумя переменными Продольные и поперечные плоские волны в однородных изотропных средах. (Лекция 2)
Продольные и поперечные плоские волны в однородных изотропных средах. (Лекция 2) Шестое математическое действие
Шестое математическое действие