Содержание
- 2. Źródło: B. Pańczyk E. Łukasik J. Sikora T. Guziak Metody Numeryczne w przykładach Wydawca: Politechnika Lubelska
- 3. Treść wykładu Numeryczne rozwiązywanie równań (metody Newtona i siecznych). Układy równań nieliniowych
- 4. Numeryczne rozwiązywanie równań
- 5. Numeryczne rozwiązywanie równań
- 6. Metoda bisekcji O funkcji f(x) z równania (5.1) zakładamy, że: jest ciągła na przedziale domkniętym ;
- 7. Metoda bisekcji
- 8. Metoda bisekcji
- 9. Metoda bisekcji
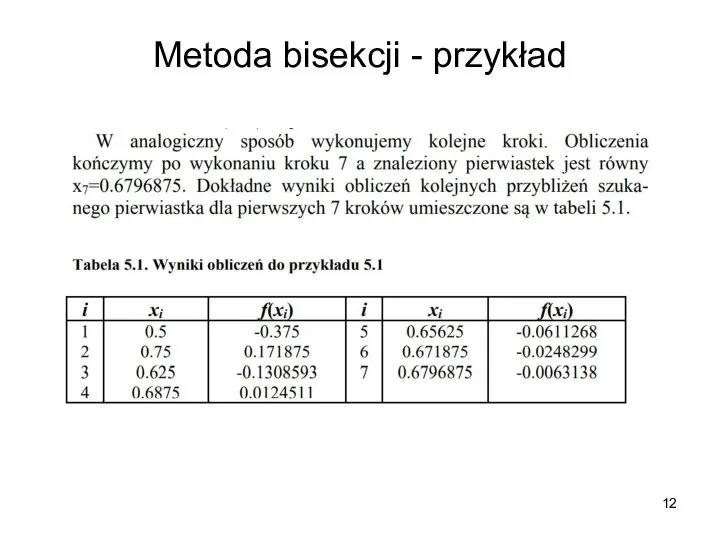
- 10. Metoda bisekcji - przykład
- 11. Metoda bisekcji - przykład
- 12. Metoda bisekcji - przykład
- 13. Metoda regula falsi Nazwa metody pochodzi od łacińskich słów: regula - linia i falsus - fałszywy.
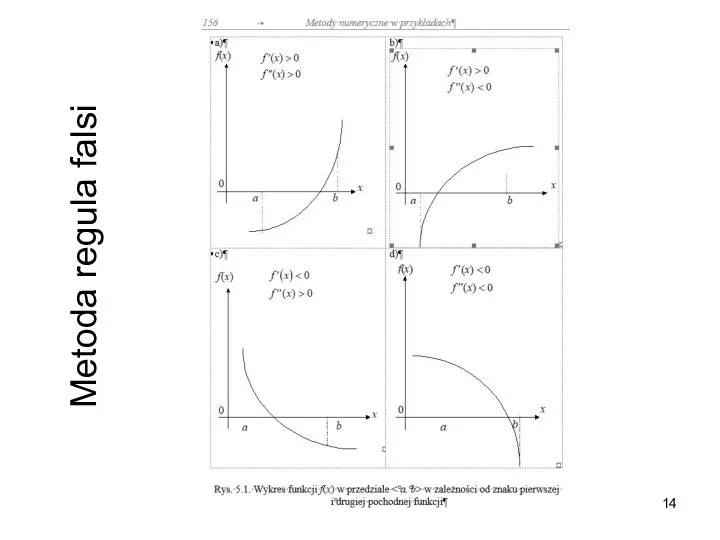
- 14. Metoda regula falsi
- 15. Metoda regula falsi
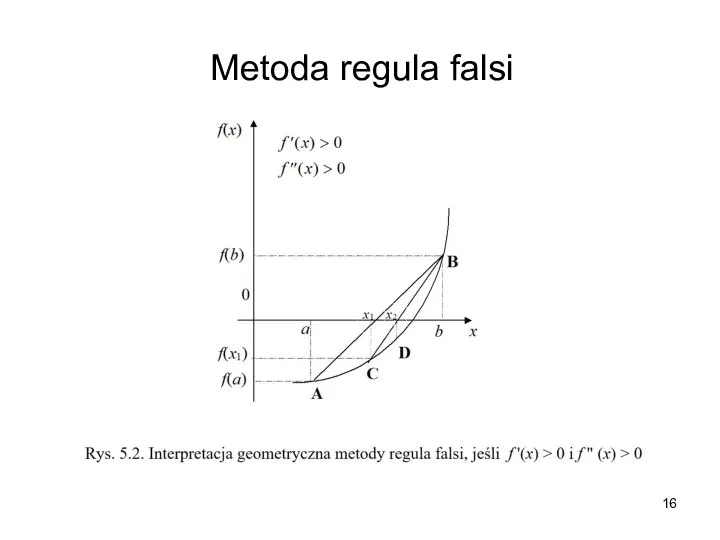
- 16. Metoda regula falsi
- 17. Metoda regula falsi
- 18. Metoda regula falsi
- 19. Metoda siecznych
- 20. Metoda siecznych
- 21. Metoda siecznych
- 22. Metoda Newtona-Raphsona
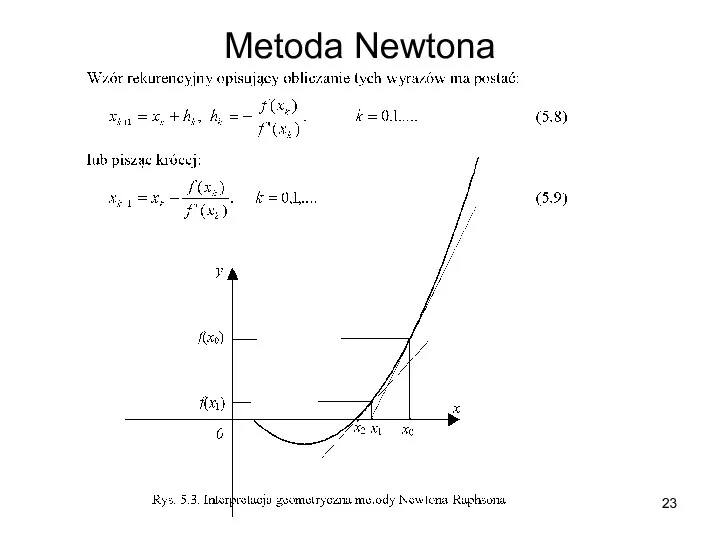
- 23. Metoda Newtona
- 24. Metoda Newtona
- 25. Metoda Newtona
- 26. Przykłady do samodzielnego rozwiązania
- 27. Przykłady do samodzielnego rozwiązania
- 28. Przykłady do samodzielnego rozwiązania
- 29. Przykłady do samodzielnego rozwiązania
- 30. Przykłady do samodzielnego rozwiązania
- 31. Przykłady do samodzielnego rozwiązania
- 32. Przykłady do samodzielnego rozwiązania
- 33. Przykłady do samodzielnego rozwiązania
- 34. Przykłady do samodzielnego rozwiązania
- 35. Przykłady do samodzielnego rozwiązania
- 36. Układy równań nieliniowych
- 37. Układy równań nieliniowych
- 38. Układy równań nieliniowych
- 39. Układy równań nieliniowych
- 40. Przykłady do samodzielnego rozwiązania
- 41. Przykłady do samodzielnego rozwiązania
- 42. Przykłady do samodzielnego rozwiązania
- 43. Przykłady do samodzielnego rozwiązania
- 45. Скачать презентацию






































 Современные методы обработки статистических данных в области спорта. Корреляция
Современные методы обработки статистических данных в области спорта. Корреляция Наибольший общий делитель и наименьшее общее кратное
Наибольший общий делитель и наименьшее общее кратное Векторы. Понятие вектора
Векторы. Понятие вектора Методы математической статистики в психологопедагогических исследованиях
Методы математической статистики в психологопедагогических исследованиях Игра-зачет Четырехугольники
Игра-зачет Четырехугольники Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Дискретные случайные величины
Дискретные случайные величины Первый признак равенства треугольников
Первый признак равенства треугольников Построение графика квадратичной функции у=ах2+bx+c, a не равно 0
Построение графика квадратичной функции у=ах2+bx+c, a не равно 0 Формулы тригонометрии
Формулы тригонометрии Методы оптимизации
Методы оптимизации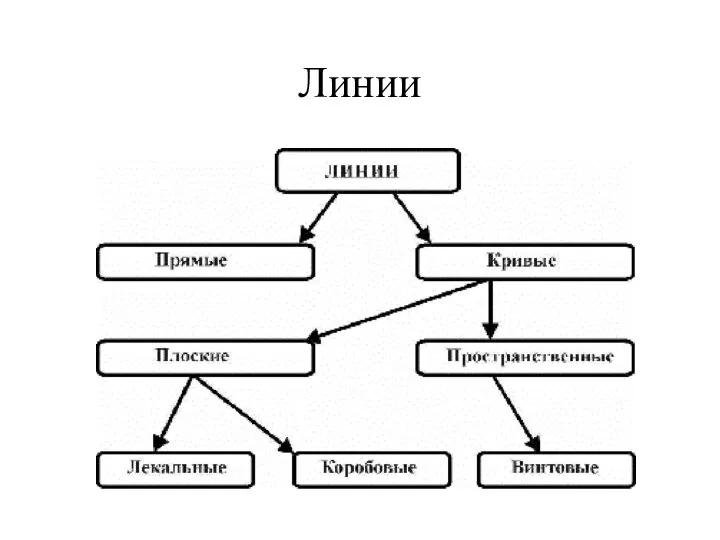 Линии. Плоские кривые. Лекальные кривые
Линии. Плоские кривые. Лекальные кривые Действия с обыкновенными дробями
Действия с обыкновенными дробями Проценты. 5 класс. Урок № 2
Проценты. 5 класс. Урок № 2 Вычисление площадей плоских фигур с помощью определенного интеграла (3)
Вычисление площадей плоских фигур с помощью определенного интеграла (3) Палочки Кюизнера. Мастер-класс. Задание 19 ЕГЭ по математике
Палочки Кюизнера. Мастер-класс. Задание 19 ЕГЭ по математике Смешанные числа
Смешанные числа Определение синуса, косинуса и тангенса угла
Определение синуса, косинуса и тангенса угла Аттестационная работа. Образовательная программа элективного курса для 9 класса Решение задач с параметром
Аттестационная работа. Образовательная программа элективного курса для 9 класса Решение задач с параметром Расстояние от точки до прямой. Перпендикулярные прямые
Расстояние от точки до прямой. Перпендикулярные прямые История возникновения дробей
История возникновения дробей Медианы, биссектрисы и высота треугольника
Медианы, биссектрисы и высота треугольника Множества. Основные понятия
Множества. Основные понятия Сложение обыкновенных дробей с одинаковым знаменателем
Сложение обыкновенных дробей с одинаковым знаменателем Среднее арифметическое
Среднее арифметическое Общие темы в математическом искусстве
Общие темы в математическом искусстве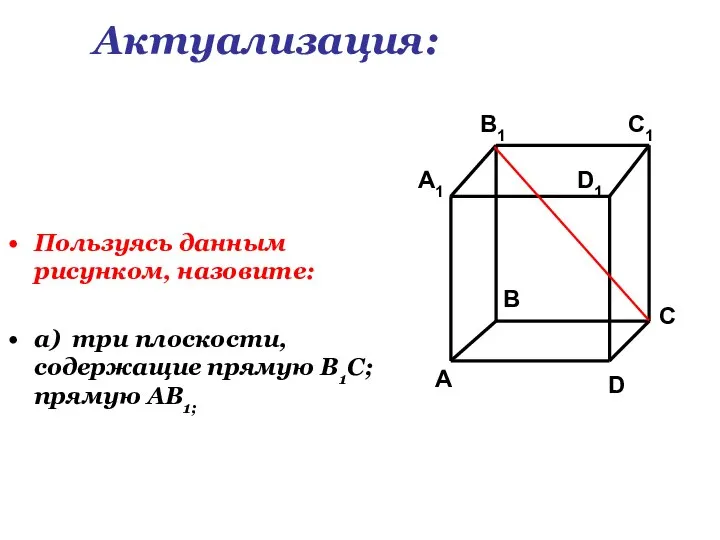 Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую
Пользуясь данным рисунком, назовите: Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую Решение задач по теме «Векторы». 9 класс
Решение задач по теме «Векторы». 9 класс