Содержание
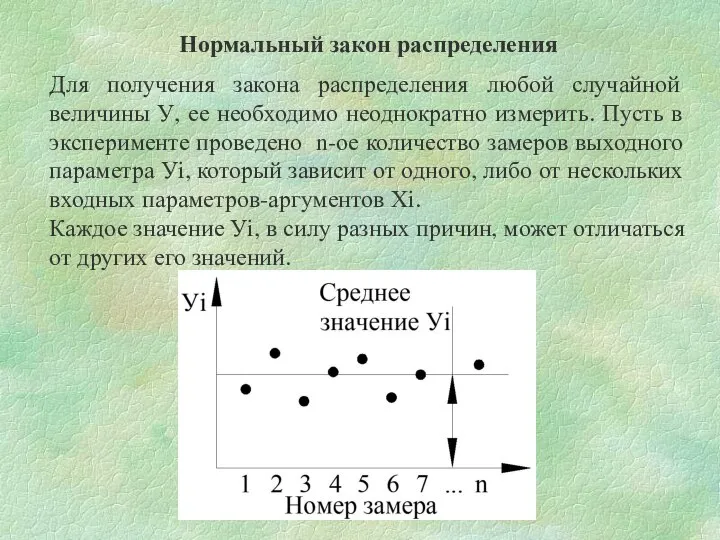
- 2. Нормальный закон распределения Для получения закона распределения любой случайной величины У, ее необходимо неоднократно измерить. Пусть
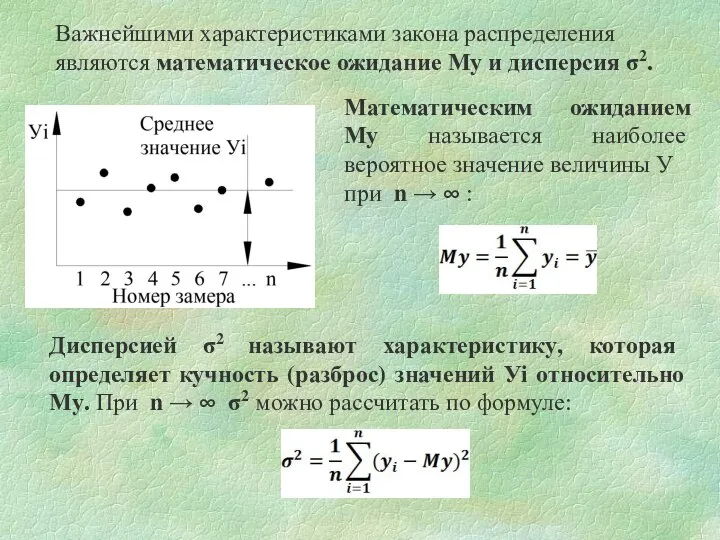
- 3. Дисперсией σ2 называют характеристику, которая определяет кучность (разброс) значений Уi относительно Му. При n → ∞
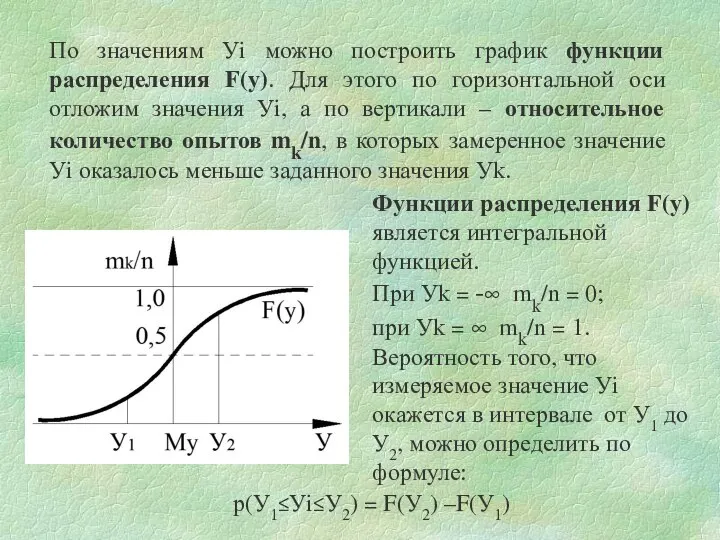
- 4. По значениям Уi можно построить график функции распределения F(у). Для этого по горизонтальной оси отложим значения
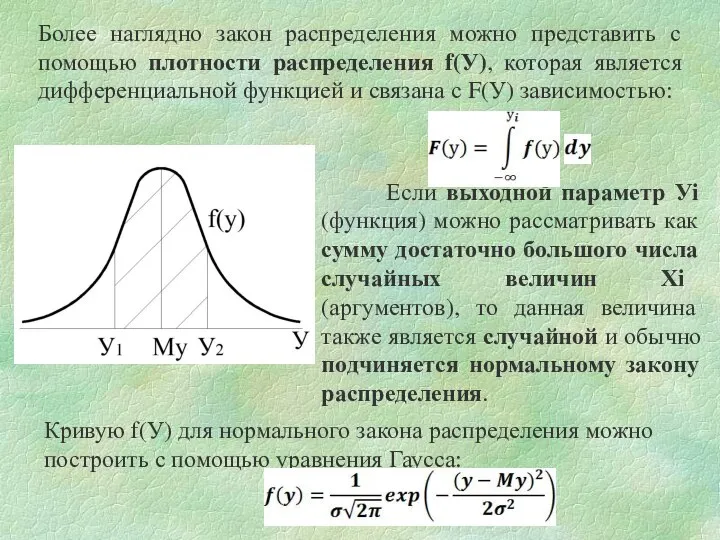
- 5. Более наглядно закон распределения можно представить с помощью плотности распределения f(У), которая является дифференциальной функцией и
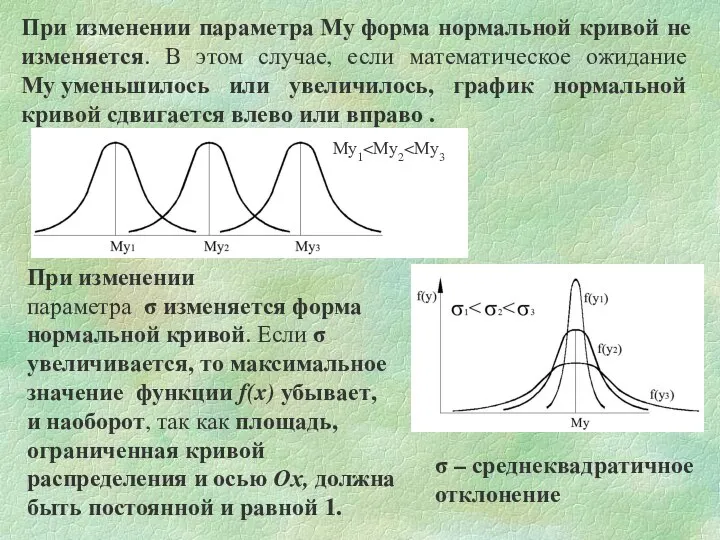
- 6. При изменении параметра Му форма нормальной кривой не изменяется. В этом случае, если математическое ожидание Му
- 7. Для реального эксперимента, т.е для случая, когда количество замеров Уi значительно меньше ∞, имеют дело с
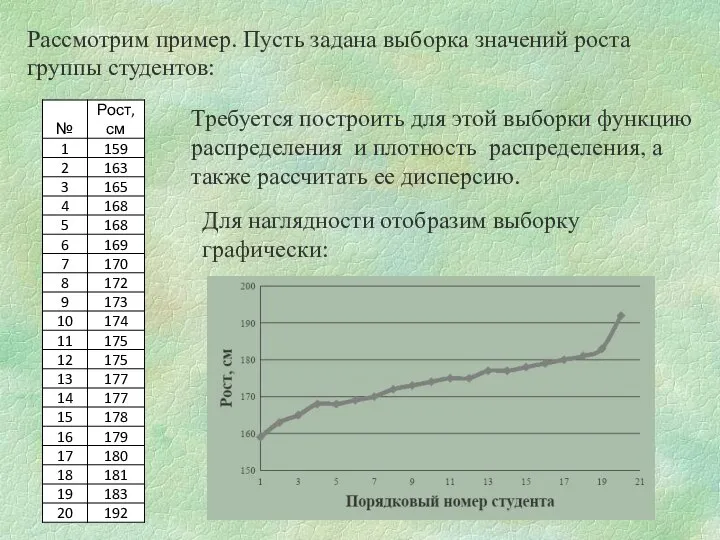
- 8. Рассмотрим пример. Пусть задана выборка значений роста группы студентов: Требуется построить для этой выборки функцию распределения
- 9. Рост студентов является исследуемой функцией. Разобьем диапазон значений представленной выборки на 10 одинаковых интервалов. Для этого:
- 11. Скачать презентацию


 Признаки параллельности прямых. Задачи на готовых чертежах
Признаки параллельности прямых. Задачи на готовых чертежах Описанная окружность
Описанная окружность Бөлінгіштіктің негізгі қасиеттері
Бөлінгіштіктің негізгі қасиеттері Множества. Круги Эйлера
Множества. Круги Эйлера Линейность изображений
Линейность изображений Аттестационная работа. Классификация квадратных трехчленов с целыми коэффициентами и данным положительным дискриминантом
Аттестационная работа. Классификация квадратных трехчленов с целыми коэффициентами и данным положительным дискриминантом Подсчёт вероятности
Подсчёт вероятности Введение в методы статистического анализа многомерных объектов
Введение в методы статистического анализа многомерных объектов Обучение младших школьников решению нестандартных олимпиадных задач
Обучение младших школьников решению нестандартных олимпиадных задач Уравнение касательной к графику функции
Уравнение касательной к графику функции Задание C1
Задание C1 Целые выражения
Целые выражения Биография Пифагора. Применение теоремы Пифагора в жизни
Биография Пифагора. Применение теоремы Пифагора в жизни Действия с десятичными дробями
Действия с десятичными дробями Математический диктант по теме «первый признак равенства треугольников». Геометрия. 7 класс
Математический диктант по теме «первый признак равенства треугольников». Геометрия. 7 класс Методологические проблемы применения математических методов в психологии. (Лекция 1)
Методологические проблемы применения математических методов в психологии. (Лекция 1) Тест по теме: "Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число". Вариант 2
Тест по теме: "Векторы в пространстве. Сложение и вычитание векторов. Умножение вектора на число". Вариант 2 Презентация по математике "Изменение величин" - скачать
Презентация по математике "Изменение величин" - скачать  Николай Иванович Лобачевский Конкурс презентаций «Великие люди России»
Николай Иванович Лобачевский Конкурс презентаций «Великие люди России»  Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Модуль числа
Модуль числа Четырехугольники. Упражнения
Четырехугольники. Упражнения Игра «Математик-бизнесмен»
Игра «Математик-бизнесмен» Математика учит точности мысли
Математика учит точности мысли Элементы симметрии правильных многогранников
Элементы симметрии правильных многогранников Правильные многоугольники
Правильные многоугольники Урок математики в 1 классе. Прибавить и вычесть число 3. Решение текстовых задач
Урок математики в 1 классе. Прибавить и вычесть число 3. Решение текстовых задач Свойства функций, непрерывных на отрезке
Свойства функций, непрерывных на отрезке