- Главная
- Математика
- Степени вершин графа. (Лекция 15)

Содержание
- 6. По степенной последовательности можно построить графы
- 7. Задача 1 Доказать, что если в графе с n вершинами (n>2) ровно две вершины имеют одинаковую
- 8. Задача 2 Существуют ли графы с данной степенной последовательностью? Ответ пояснить. 1) (1;2;3;4); 2) (13;22;3;5); 3)
- 9. Задача 3 а) Опишите n вершинный однородный граф степени 2. б) Опишите n вершинный однородный граф
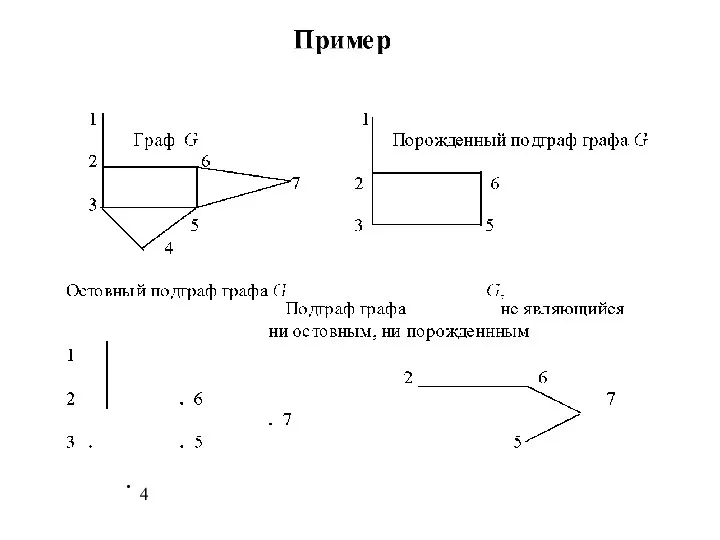
- 10. Подграфы. Операции над графами
- 13. 4
- 24. Скачать презентацию
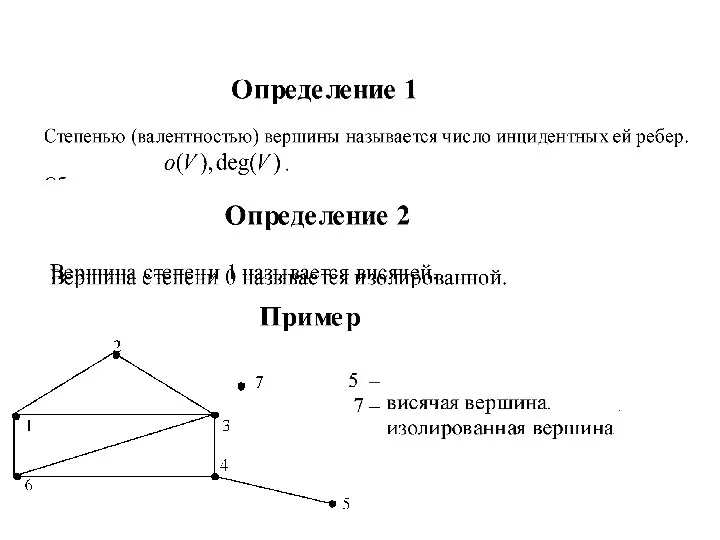
Слайд 2
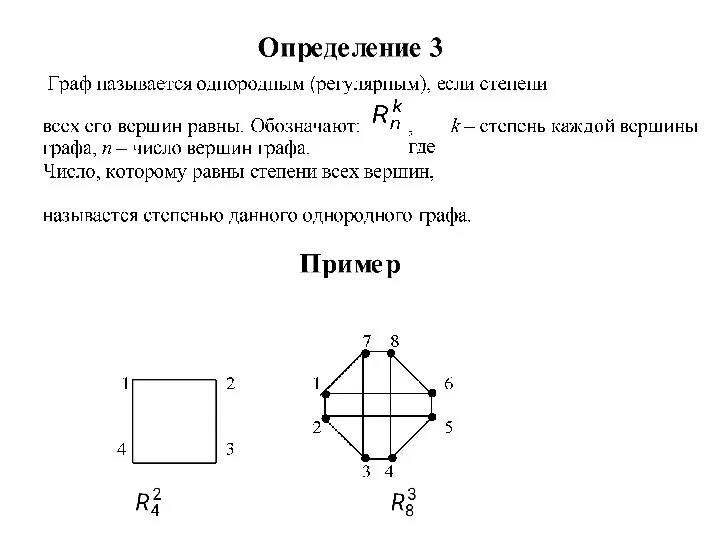
Слайд 3
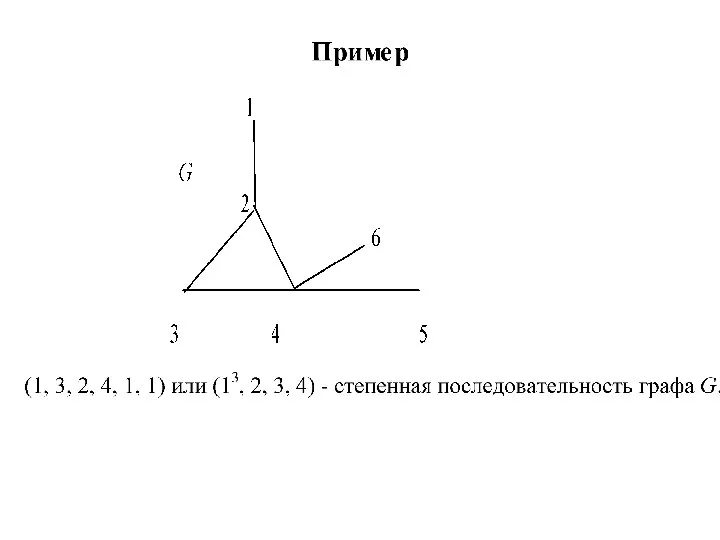
Слайд 4
Слайд 5
Слайд 6
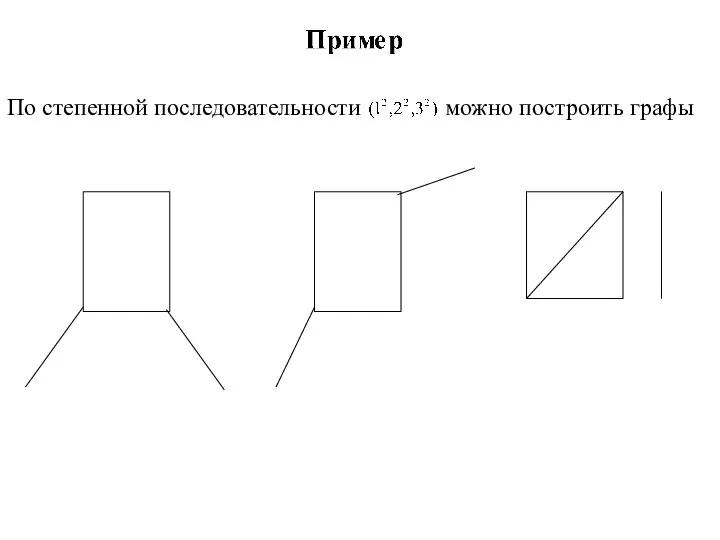
По степенной последовательности можно построить графы
По степенной последовательности можно построить графы
Слайд 7
Задача 1
Доказать, что если в графе с n вершинами (n>2)
ровно две
Задача 1
Доказать, что если в графе с n вершинами (n>2)
ровно две
вершины имеют одинаковую степень,
то в этом графе либо в точности одна вершина степени 0,
либо в точности одна вершина степени (n-1).
Решение. Допустим противное.
1) В графе ровно две вершины одинаковой степени, и это вершины степени 0. Тогда, удалив из графа эти изолированные вершины, получим граф, степени всех вершин которого различны, что невозможно по теореме 3.
2) Если же в графе ровно две вершины одинаковой степени, и это вершины степени (n-1), то перейдя к дополнению , получим противоречие, аналогично пункту 1).
то в этом графе либо в точности одна вершина степени 0,
либо в точности одна вершина степени (n-1).
Решение. Допустим противное.
1) В графе ровно две вершины одинаковой степени, и это вершины степени 0. Тогда, удалив из графа эти изолированные вершины, получим граф, степени всех вершин которого различны, что невозможно по теореме 3.
2) Если же в графе ровно две вершины одинаковой степени, и это вершины степени (n-1), то перейдя к дополнению , получим противоречие, аналогично пункту 1).
Слайд 8
Задача 2
Существуют ли графы с данной степенной последовательностью? Ответ пояснить.
1) (1;2;3;4);
2)
Задача 2
Существуют ли графы с данной степенной последовательностью? Ответ пояснить.
1) (1;2;3;4);
2)
(13;22;3;5);
3) (0;1;2;3;42);
4) (12;23;32;4);
5) (12;32;4).
Решение.
1) Не существует, так как все степени различные (смотри теорему 7).
2) Не существует, так как число вершин нечетной степени нечетно, а именно 5 ( смотри теорему 6).
3) Не существует(смотри задачу 1).
4) Построим граф, имеющий данную степенную последовательность
5) Не существует, так как, соединив вершину степени 4 с четырьмя из оставшихся вершин, убеждаемся, что для вершин степени 3 не достаточно смежных вершин.
3) (0;1;2;3;42);
4) (12;23;32;4);
5) (12;32;4).
Решение.
1) Не существует, так как все степени различные (смотри теорему 7).
2) Не существует, так как число вершин нечетной степени нечетно, а именно 5 ( смотри теорему 6).
3) Не существует(смотри задачу 1).
4) Построим граф, имеющий данную степенную последовательность
5) Не существует, так как, соединив вершину степени 4 с четырьмя из оставшихся вершин, убеждаемся, что для вершин степени 3 не достаточно смежных вершин.
Слайд 9
Задача 3
а) Опишите n вершинный однородный граф степени 2.
б) Опишите n
Задача 3
а) Опишите n вершинный однородный граф степени 2.
б) Опишите n
вершинный однородный граф степени n-1.
Решение.
а) Многоугольник с n вершинами.
б) Полный n вершинный граф.
Решение.
а) Многоугольник с n вершинами.
б) Полный n вершинный граф.
Слайд 10
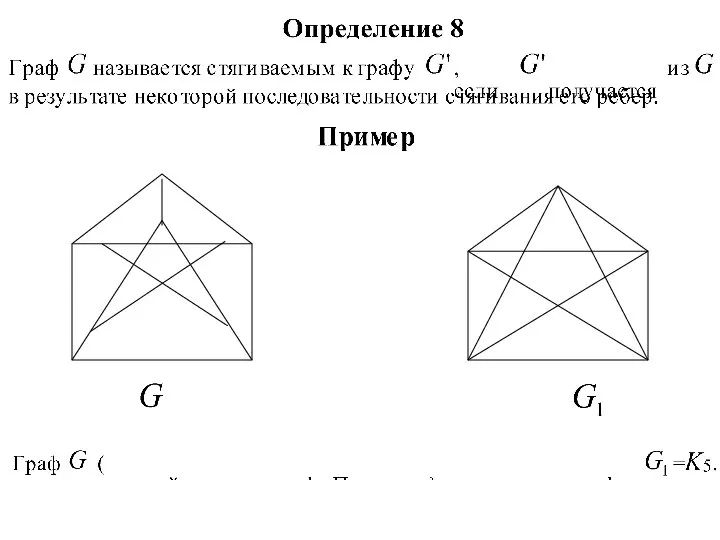
Подграфы.
Операции над графами
Подграфы.
Операции над графами
Слайд 11
Слайд 12
Слайд 13
4
4
Слайд 14
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Слайд 19
Слайд 20
Слайд 21
Слайд 22










 Тренажёр «Веселая пчёлка». Математика 1 класс
Тренажёр «Веселая пчёлка». Математика 1 класс Умножение десятичной дроби на натуральное число
Умножение десятичной дроби на натуральное число Длина ломаной линии
Длина ломаной линии Задача экономического содержания в ЕГЭ № 19
Задача экономического содержания в ЕГЭ № 19 Основные законы распределения случайных величин
Основные законы распределения случайных величин Надежность производственных и технологических систем. Математические модели в теории надежности
Надежность производственных и технологических систем. Математические модели в теории надежности Решение задач на комбинации многогранников и тел вращения
Решение задач на комбинации многогранников и тел вращения Дроби. Нахождение части числа
Дроби. Нахождение части числа Прямоугольный параллелепипед. 5 класс
Прямоугольный параллелепипед. 5 класс Неделя математики в школе
Неделя математики в школе Процентные расчёты
Процентные расчёты Квадратный корень из произведения и дроби. 8 класс
Квадратный корень из произведения и дроби. 8 класс Логарифмическая функция
Логарифмическая функция Сумма n первых членов арифметической прогрессии
Сумма n первых членов арифметической прогрессии Конструктор (1)
Конструктор (1) Активизация творческой деятельности учащихся на уроках математики с использованием ИКТ
Активизация творческой деятельности учащихся на уроках математики с использованием ИКТ Зигзаг удачи. Городская математическая игра
Зигзаг удачи. Городская математическая игра Угол между прямыми. Подготовка к ЕГЭ С2
Угол между прямыми. Подготовка к ЕГЭ С2 Практикум №2 по решению стереометрических задач. (Задания 13 и 16, базового уровня)
Практикум №2 по решению стереометрических задач. (Задания 13 и 16, базового уровня) Стохастическая модель
Стохастическая модель ЕГЭ по алгебре, 11 класс
ЕГЭ по алгебре, 11 класс Формулы площади полной поверхности
Формулы площади полной поверхности Пропорциональные отрезки в прямоугольном треугольнике
Пропорциональные отрезки в прямоугольном треугольнике Взаимное расположение прямой и окружности
Взаимное расположение прямой и окружности Древние меры длины Исследовательская работа Автор: Панфёров Михаил
Древние меры длины Исследовательская работа Автор: Панфёров Михаил Действия с числами
Действия с числами Осевая и центральная симметрия. Симметрия в природе
Осевая и центральная симметрия. Симметрия в природе Разложение чисел на простые множители
Разложение чисел на простые множители