Содержание
- 2. M(X) = ∫ xf(x)dx = a; D(X) = ∫ x2 f(x)dx – a2 = σ2. Интегральная
- 3. Свойства функции f(x) y = 1. x € (-∞;∞); 2. lim f(x) = 0; x +∞
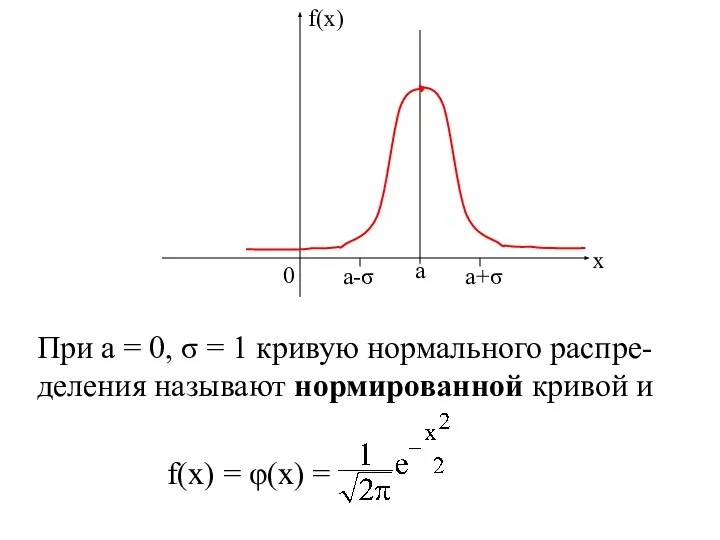
- 4. ymax = f(a) = 4. График y = f(x) симметричен относительно прямой x = a. 5.
- 5. a a-σ a+σ При a = 0, σ = 1 кривую нормального распре-деления называют нормированной кривой
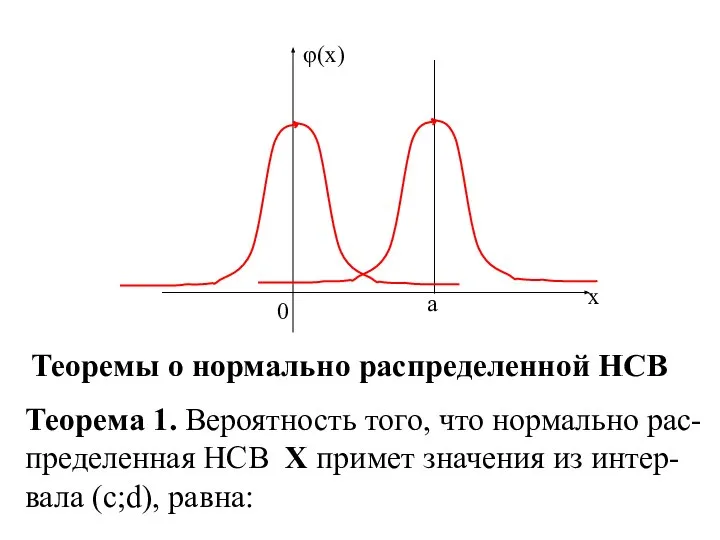
- 6. Теоремы о нормально распределенной НСВ Теорема 1. Вероятность того, что нормально рас-пределенная НСВ Х примет значения
- 7. P( c ≤ X ≤ d ) = (Φ ( ) - Φ ( )) Теорема
- 8. среднего квадратического отклонения: P ( X – M(X) ) = Φ ( 3 ) = 0.9973
- 9. Дано: а =100, σ =5 P= 0,9973 c ≤ X ≤ d c, d - ?
- 10. (*Из пункта ведётся стрельба из орудия вдоль прямой. Предполагается, что дальность полёта распределена нормально с математическим
- 11. (* Диаметр подшипников, изготовленные на заводе, представляет собой случайную величину,распределенную нормально с математическим ожиданием 1,5 см
- 12. 1) варьирование СВ обусловлено воздействием большого числа факторов; 2) эти факторы независимы и заданы произ- вольными
- 13. сумма N независимых СВ, заданных произ-вольными распределениями, по мере возрас-тания числа N стремится к нормальному. Биномиальное
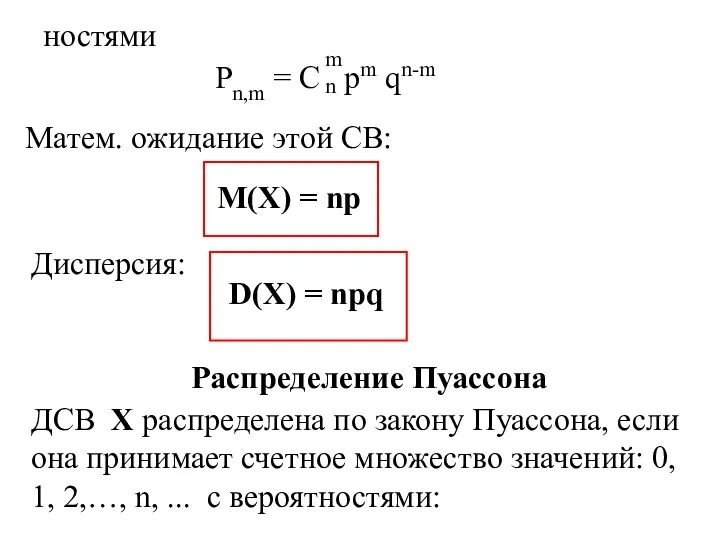
- 14. ностями m n Pn,m = C pm qn-m Матем. ожидание этой СВ: M(X) = np Дисперсия:
- 15. Pm = am* Если СВ Х – число наступлений события А с вероятностью p 0 в
- 16. Распределение Пуассона применяется, когда n порядка нескольких сотен и больше, а 1≤ np ≤ 10. Задача.
- 17. Если СВ Х распределена по закону Пуассона, то M(X) = D(X) = np = a Простейший
- 18. жуток времени Δt зависит только от числа k и от промежутка Δt, и не зависит от
- 19. стью потока и обозначается λ. Тогда - средний промежуток времени между двумя последовательными событиями в простейшем
- 20. нарных потоков, каждый из которых мало влияет на сумму, образует поток, близкий к простейшему. Задача. Интенсивность
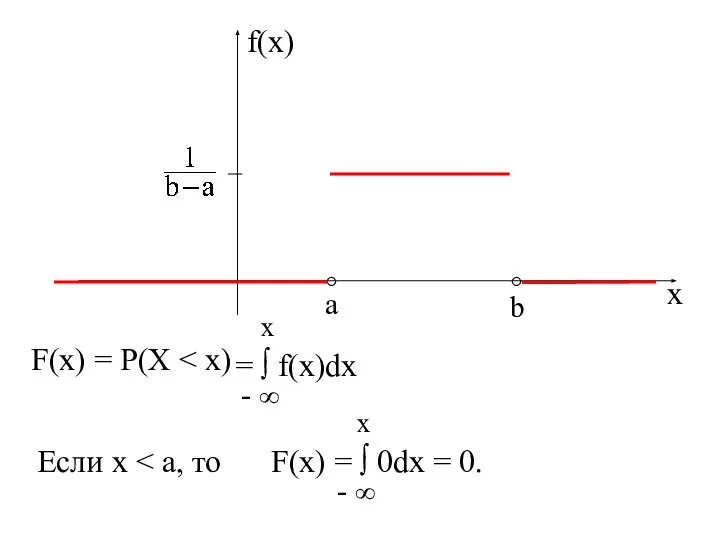
- 21. Равномерное распределение Определение. НСВ Х имеет равномерное распределение на отрезке [a; b], если ее плотность распределения
- 22. = ∫ 0dx + ∫ Cdx + ∫ 0dx = 0 + Cx│+ 0 = C(b
- 23. x f(x) F(x) = P(X = ∫ f(x)dx Если x F(x) = ∫ 0dx = 0.
- 24. Если a F(x)= ∫ f(x)dx +∫ f(x)dx = ∫ 0dx +∫ dx = 0+ x│ =
- 25. x F(x) M(X) = ∫ xf(x)dx = ∫ dx = • │ = D(X)= ∫ x2f(x)dx
- 26. не меньшие α, но не большие β (причем [α;β] € [a;b] ), равна: P( α ≤
- 27. в некоторый момент TV, будет смотреть любимый сериал без перерыва на рекламу а) не менее 8,
- 28. Задача. Цена деления шкалы прибора равна 0,1. Показания прибора округляют до ближайшего деления. Найти вероятность того,
- 29. Показательное распределение Определение. НСВ Х распределена по показа-тельному закону распределения, если плотность ее распределения f (x)
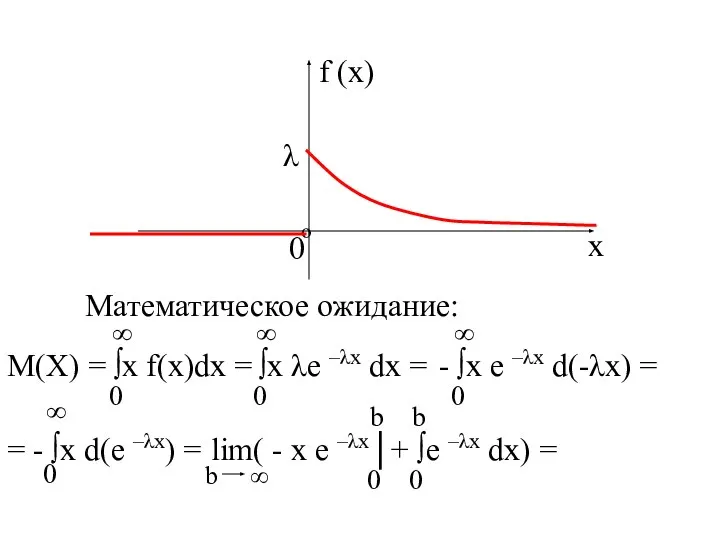
- 30. f (x) º λ Математическое ожидание: М(Х) = ∫х f(x)dx = ∫х λe –λx dx =
- 31. = - lim b ∞ - lim b ∞ (e –λb – 1) = 0 +
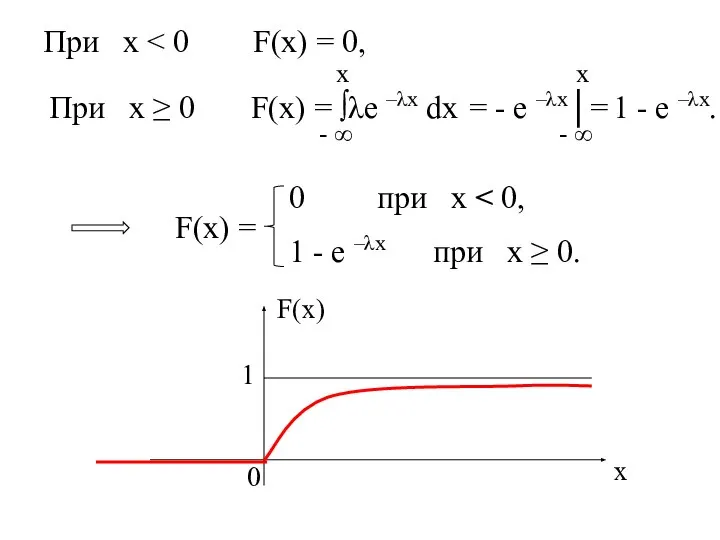
- 32. При х При х ≥ 0 F(x) = ∫λe –λx dx = - e –λx│= 1
- 33. Вероятность того, что НСВ Х, распределенная по показательному закону, примет значения из промежутка [а; b], равна:
- 34. Дано: = 8 λ = а = 6 b = 10 P(6 ≤ X ≤10)=? СВ
- 35. одного и того же маршрута, между двумя звонка- ми на станцию скорой помощи, между двумя поломками
- 36. противоположным событию X P(X > x) + P(X Отсюда: P(X > x) = 1 - P(X
- 38. Скачать презентацию


















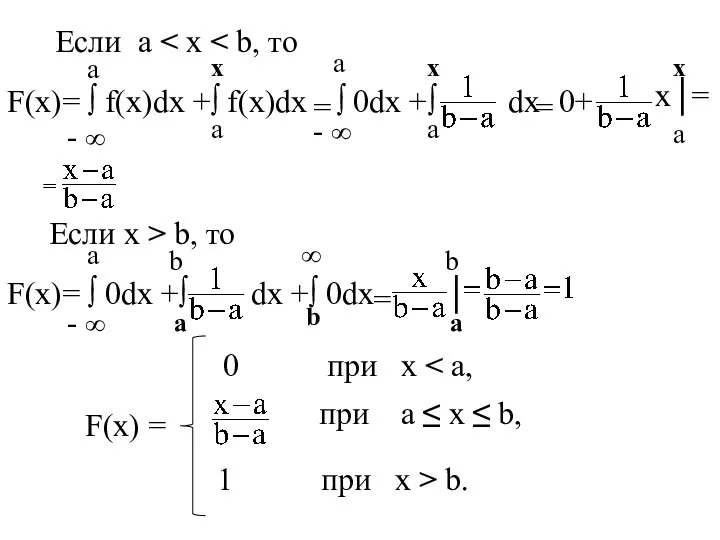

![не меньшие α, но не большие β (причем [α;β] € [a;b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1460757/slide-25.jpg)








 Объём прямоугольного параллелепипеда. Единицы объёма
Объём прямоугольного параллелепипеда. Единицы объёма Комплексные числа
Комплексные числа Презентация по математике "Сложение отрицательных чисел и чисел с разными знаками" - скачать
Презентация по математике "Сложение отрицательных чисел и чисел с разными знаками" - скачать  Множество и его элементы
Множество и его элементы Линейная функция и ее график
Линейная функция и ее график Инварианты. Общее уравнение кривой второго порядка
Инварианты. Общее уравнение кривой второго порядка Разложение многочленов на множители
Разложение многочленов на множители Теория погрешностей, случайные и систематические погрешности
Теория погрешностей, случайные и систематические погрешности Решение текстовых задач. Урок - путешествие 6 класс
Решение текстовых задач. Урок - путешествие 6 класс Сумма углов в треугольнике
Сумма углов в треугольнике Обыкновенные дроби
Обыкновенные дроби Тождества. Следствие и равносильность равенств
Тождества. Следствие и равносильность равенств Приложение дифференциала к приближенным вычислениям
Приложение дифференциала к приближенным вычислениям Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия
Статистические методы, оценивающие факторные эффекты и эффекты межфакторного взаимодействия Оценка качества модели парной линейной регрессии
Оценка качества модели парной линейной регрессии Прямоугольный параллелепипед
Прямоугольный параллелепипед Свойства логарифмов
Свойства логарифмов Параллельный перенос и его свойства
Параллельный перенос и его свойства МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №2 Цифровой образовательный ресу
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №2 Цифровой образовательный ресу Решение систем уравнений второй степени. 9 класс
Решение систем уравнений второй степени. 9 класс Сечение тетраэдра
Сечение тетраэдра Исследование функции и построение графика
Исследование функции и построение графика Применение формул сокращенного умножения
Применение формул сокращенного умножения Аттестационная работа. Методическая разработка по выполнению проектной работы «Как измерить удава»
Аттестационная работа. Методическая разработка по выполнению проектной работы «Как измерить удава» Числовые функции (Количество и сумма натуральных делителей числа. Функция Эйлера). Лекция 2
Числовые функции (Количество и сумма натуральных делителей числа. Функция Эйлера). Лекция 2 Текше және тікбұрышты паралелепипед
Текше және тікбұрышты паралелепипед Точки разрыва функции и их классификация
Точки разрыва функции и их классификация Деление числа на произведение. Деление с остатком на 10, 100, 1000
Деление числа на произведение. Деление с остатком на 10, 100, 1000