Содержание
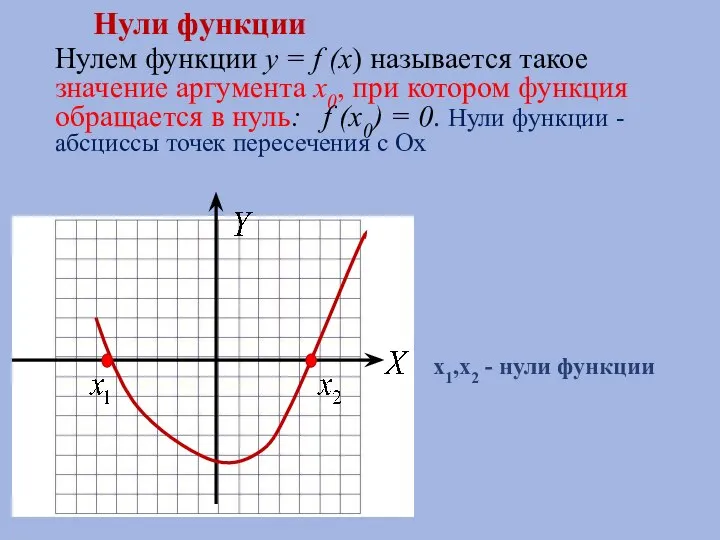
- 2. Нулем функции y = f (x) называется такое значение аргумента x0, при котором функция обращается в
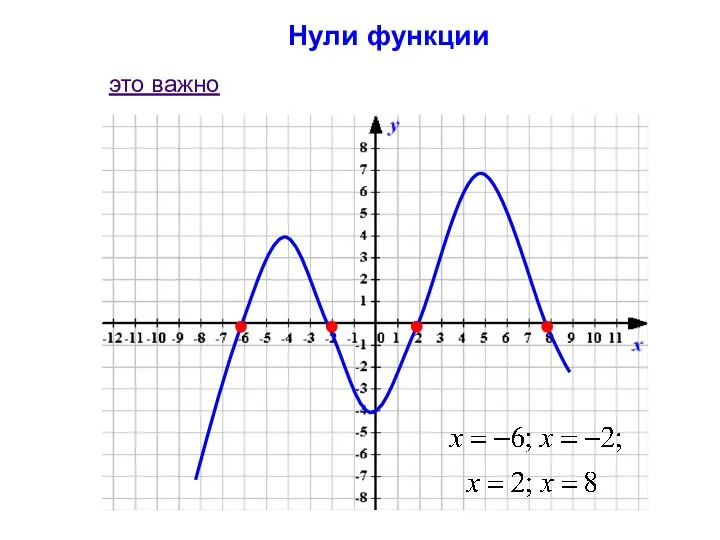
- 3. Нули функции это важно
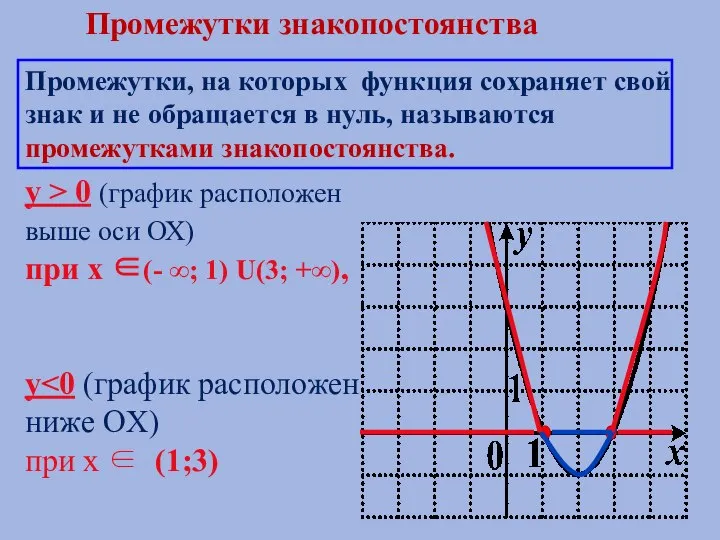
- 4. Промежутки, на которых функция сохраняет свой знак и не обращается в нуль, называются промежутками знакопостоянства. y
- 5. Промежутки знакопостоянства функции Это промежутки, на которых функция y(х) принимает положительные (отрицательные) значения.
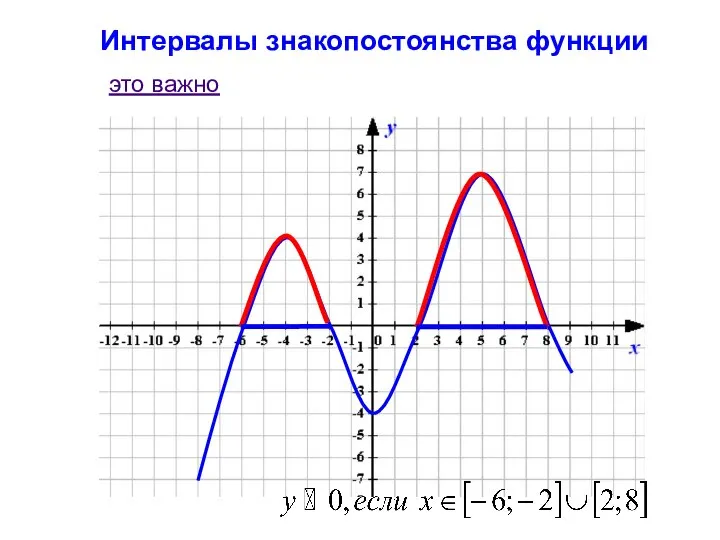
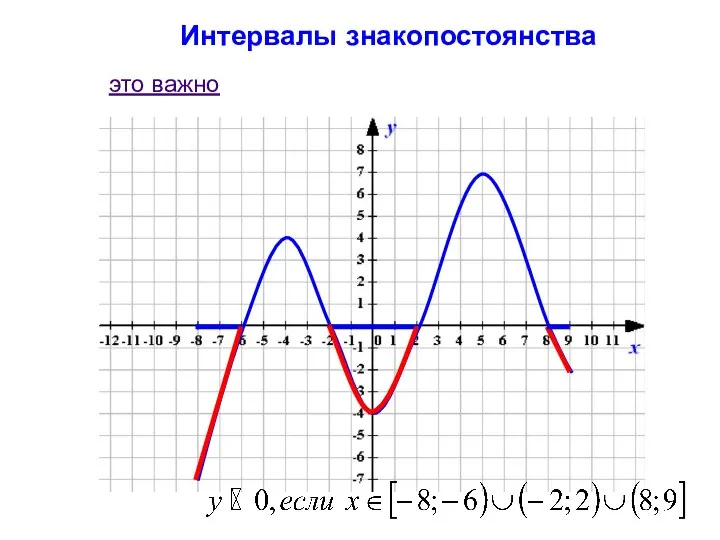
- 6. Интервалы знакопостоянства функции это важно
- 7. Интервалы знакопостоянства это важно
- 8. Функцию у = f(х) называют возрастающей на множестве Х, если для любых двух точек х1 и
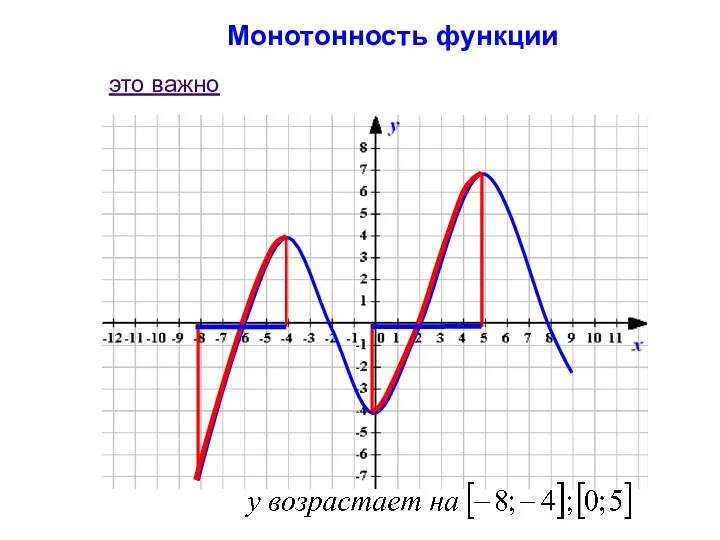
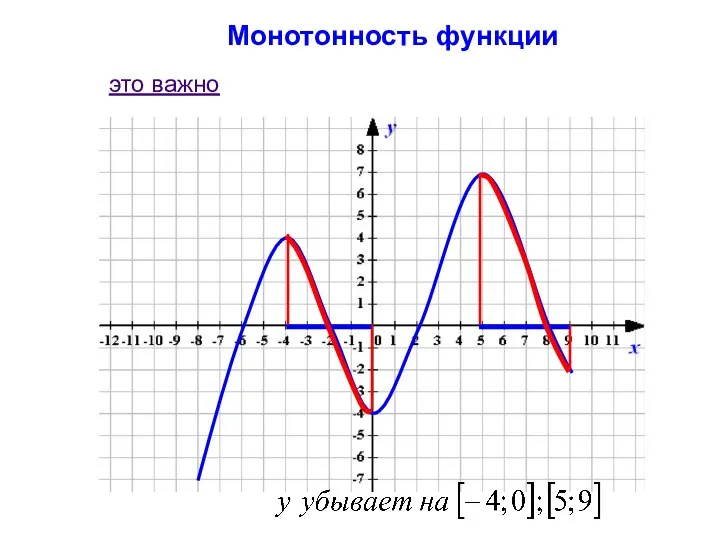
- 9. Монотонность функции Функция y(х) убывает на множестве P, если для любых x1 и x2 из множества
- 10. Монотонность функции это важно
- 11. Монотонность функции это важно
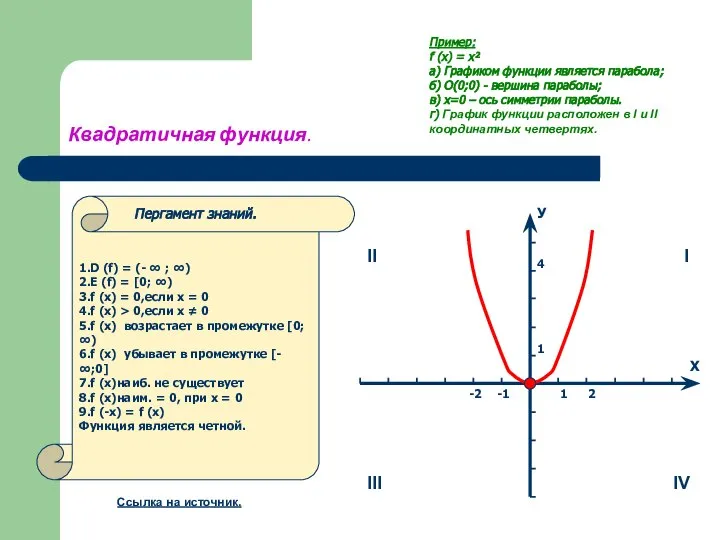
- 12. Квадратичная функция. У Х -2 -1 1 2 1 4 Пример: f (x) = х² а)
- 13. Степенная функция с натуральным показателем. Пример: f (x) = x³. а)Графиком функции является кубическая парабола б)График
- 14. Линейная функция. 1.D (f) = (- ∞;∞) 2.E (f) = ( - ∞;∞) 3.f (x) =
- 15. Прямая пропорциональность. Пример: f (x) = kx, k>0 а)Графиком функции является прямая; б)График функции проходит через
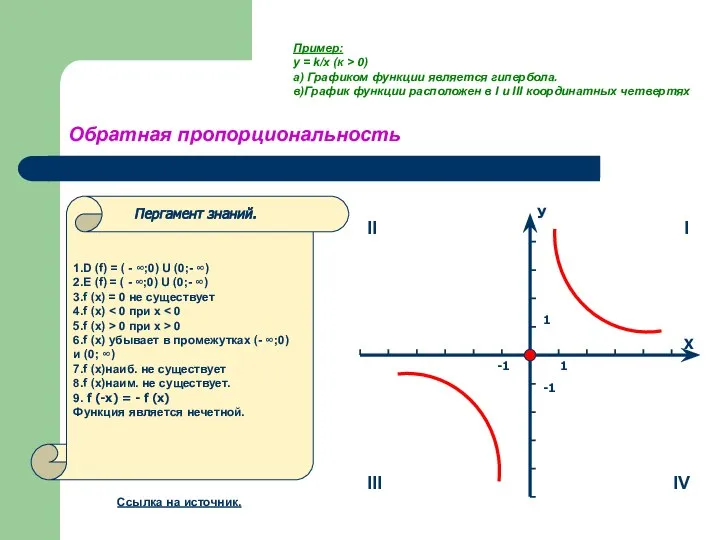
- 16. Обратная пропорциональность 1.D (f) = ( - ∞;0) U (0;- ∞) 2.E (f) = ( -
- 18. Скачать презентацию






 МАТЕМАТИКА ТЕСТ СОСТАВИЛА УЧЕНИЦА 4 Б КЛАССА ВЯЗОВА ЛУИЗА.
МАТЕМАТИКА ТЕСТ СОСТАВИЛА УЧЕНИЦА 4 Б КЛАССА ВЯЗОВА ЛУИЗА. Дискретная математика. Деревья. Определения дерева
Дискретная математика. Деревья. Определения дерева Раскрытие скобок
Раскрытие скобок Поиск экстремальных конфигураций в геометрических задачах при помощи библиотеки PyTorch
Поиск экстремальных конфигураций в геометрических задачах при помощи библиотеки PyTorch Презентация по математике "Сложение и вычитание двузначных чисел" - скачать
Презентация по математике "Сложение и вычитание двузначных чисел" - скачать  Взаимное положение прямых и плоскостей
Взаимное положение прямых и плоскостей Урок математики в 6 классе Автор презентации учитель МОУ «Новотроицкая СОШ» Тукаевского района Республики Татарстан Гусева Гуль
Урок математики в 6 классе Автор презентации учитель МОУ «Новотроицкая СОШ» Тукаевского района Республики Татарстан Гусева Гуль Длина окружности
Длина окружности Властивості предметів. Порівняння чисел і предметів. Знаки <, >, =
Властивості предметів. Порівняння чисел і предметів. Знаки <, >, = Программа элективного курса «Проценты в нашей жизни»
Программа элективного курса «Проценты в нашей жизни» Решение уравнений в системе Maxima
Решение уравнений в системе Maxima Муниципальное бюджетное образовательное учреждение Ясногорская средняя общеобразовательная школа УРОК МАТЕМАТИКИ тема: «Взаи
Муниципальное бюджетное образовательное учреждение Ясногорская средняя общеобразовательная школа УРОК МАТЕМАТИКИ тема: «Взаи Обыкновенные дроби. Правило умножения обыкновенных дробей
Обыкновенные дроби. Правило умножения обыкновенных дробей Математическая статистика (лекция 6)
Математическая статистика (лекция 6) Рисование узора из геометрических фигур
Рисование узора из геометрических фигур Решение задач, приводящих к умножению дробей
Решение задач, приводящих к умножению дробей Математика. Урок №76
Математика. Урок №76 Свойства прямоугольного треугольника. Геометрия 7 класс
Свойства прямоугольного треугольника. Геометрия 7 класс Презентация по математике "Путешествие во времени" - скачать
Презентация по математике "Путешествие во времени" - скачать  Функции
Функции Элементы математического анализа. Введение
Элементы математического анализа. Введение Своя Игра по геометрии
Своя Игра по геометрии Многочлен и его стандартный вид
Многочлен и его стандартный вид Аттестационная работа. Программа учебного курса по математике для 7 класса «Решение логических и исследовательских задач»
Аттестационная работа. Программа учебного курса по математике для 7 класса «Решение логических и исследовательских задач» Задача о трех игральных костях. Элементарный способ
Задача о трех игральных костях. Элементарный способ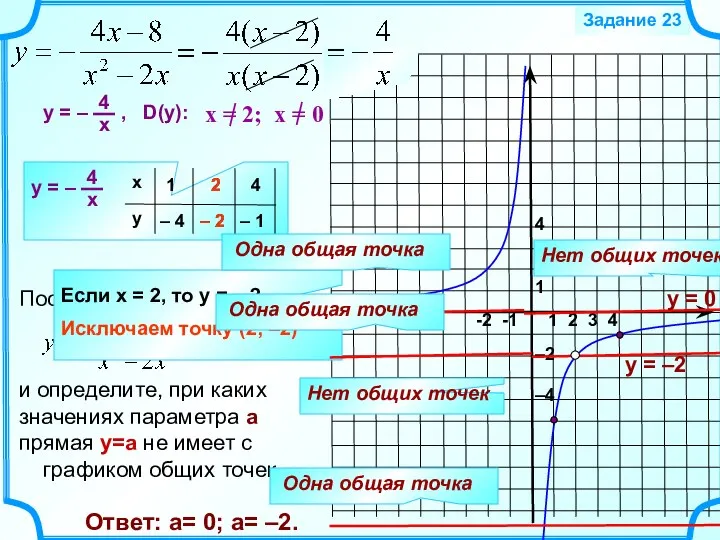 Гипербола с проколотой точкой. Часть II
Гипербола с проколотой точкой. Часть II Задания командам. Треугольники. (7 класс)
Задания командам. Треугольники. (7 класс) Основы теории вероятностей
Основы теории вероятностей