Содержание
- 2. Виет Франсуа родился в 1540 году в Фонте-ле-Конт французской провинции Пуату – Шарант. Отец Виета был
- 3. Получив юридическое образование, он с девятнадцати лет успешно занимался адвокатской практикой в родном городе. Он был
- 4. Виет сделал принципиально новое открытие, поставив перед собой цель изучать не числа, а действия над ними.
- 5. Виет сначала решает задачи в общем виде, и только потом приводит числовые параметры. В общей части
- 6. Теорема Виета Сумма корней приведённого квадратного уравнения x2 + px + q = 0 равна коэффициенту
- 7. Особый интерес представляет исследование Виета по составлению уравнений из линейных множителей и по установлению связей между
- 8. Пусть x1 и x2 – корни приведенного квадратного уравнения x2 + px + q = 0
- 9. Выполняя аналогичные действия для приведенного кубического уравнения x3+ax2+bx+c=0, считая x1,x2,x3 корнями исходного кубического уравнения, получаем: (х-x1)(х-x2)(х-x3)
- 10. Если x1,x2,x3,- корни неприведённого кубического уравнения ax3 + bx2 + cx + d = 0, то
- 11. Решить уравнение x3-4x2+x+6=0. 1 способ: при а=1 свободный член этого уравнения раскладывают на простые множители, затем
- 12. 2 способ: применение теоремы Виета для решения кубического уравнения Итак, если х3-4х2+х+6=0, то х1+х2+х3=4 Х1*х2+х1*х3+х2*х3=1, Х1*х2*х3=-6
- 13. Задача: вычислить, используя теорему Виета, сумму квадратов корней уравнения х3-6х2+11х-6=0 Согласно теореме Виета имеем: х1+х2+х3=6 х1*х2+х1*х3+х2*х3=11
- 14. Задача: Составить кубическое уравнение, корнями которого являются числа -5;3;4 Решение: Пусть х1=-5, х2=3,х3=4, тогда А теперь
- 15. Посвящение теореме Виета: По праву достойна в стихах быть воспета О свойствах корней теорема Виета. Что
- 17. Скачать презентацию














 Применение средств ЭВМ при обработке данных активного эксперимента
Применение средств ЭВМ при обработке данных активного эксперимента Свойства определенного интеграла
Свойства определенного интеграла Построение диаграмм и графиков
Построение диаграмм и графиков Урок математики 2 класс Шаршукова В.А., учитель начальных классов МАОУСОШ № 8 г.Старая Русса
Урок математики 2 класс Шаршукова В.А., учитель начальных классов МАОУСОШ № 8 г.Старая Русса Умножение обыкновенных дробей. 6 класс
Умножение обыкновенных дробей. 6 класс Проверка статистических гипотез (лекция 8)
Проверка статистических гипотез (лекция 8) Симметрия в окружающем мире. Симметрия в человеческом творчестве. Орнаменты
Симметрия в окружающем мире. Симметрия в человеческом творчестве. Орнаменты Урок - морское путешествие. Дробные выражения
Урок - морское путешествие. Дробные выражения Путешествие в сказку математика
Путешествие в сказку математика Различие треугольников по длинам сторон и по видам углов
Различие треугольников по длинам сторон и по видам углов Линейность изображений
Линейность изображений ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК
ПРОБЛЕМЫ СИСТЕМАТИЧЕСКИХ И СЛУЧАЙНЫХ ОШИБОК  Презентация по математике "Системы исчисления" - скачать бесплатно
Презентация по математике "Системы исчисления" - скачать бесплатно Презентация по математике "Тригонометрические функции числового аргумента" - скачать
Презентация по математике "Тригонометрические функции числового аргумента" - скачать  «Преобразование целого выражения в многочлен» Подготовила учитель математики Гомонова Галина Васильевна
«Преобразование целого выражения в многочлен» Подготовила учитель математики Гомонова Галина Васильевна Квадратные уравнения. 8 класс
Квадратные уравнения. 8 класс Игры Мудрой Совы
Игры Мудрой Совы Статистическая обработка вариационного ряда
Статистическая обработка вариационного ряда Центральные и вписанные углы
Центральные и вписанные углы Числовая окружность
Числовая окружность Метрические пространства
Метрические пространства Круг и отрезок
Круг и отрезок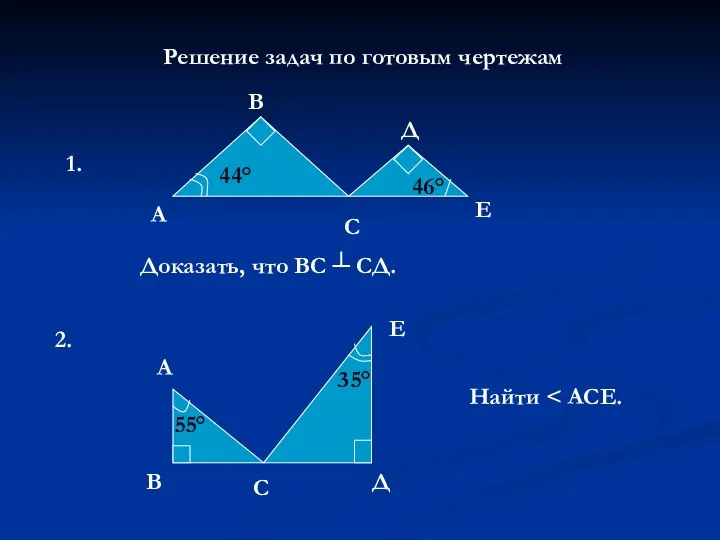 Прямоугольные треугольники. Решение задач по готовым чертежам
Прямоугольные треугольники. Решение задач по готовым чертежам Задачи на построение треугольника. Урок геометрии в 7 классе
Задачи на построение треугольника. Урок геометрии в 7 классе Вимірювальні прибори
Вимірювальні прибори Система однородных линейных уравнений
Система однородных линейных уравнений Тренажёр. Таблица умножения. «Юные водители»
Тренажёр. Таблица умножения. «Юные водители» Обернена тригонометрична функція y=arcsinx
Обернена тригонометрична функція y=arcsinx