Содержание
- 2. Девиз : « Не делай никогда того, чего не знаешь , но научись всему, что следует
- 3. С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π] для следующих выражений arcsin 0,
- 4. Верно ли равенство
- 5. Имеет ли смысл выражение:
- 6. «Верно - неверно». 1) sin2x+cos2x=1 – основное тригонометрическое тождество? 2) [-1;1] – область значения функций sinx
- 7. «Верно - неверно» ОТВЕТЫ нет да да нет нет да нет да да нет
- 8. Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из
- 9. Решение простейших тригонометрических уравнений.
- 10. * 2) уметь определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности; 4) знать
- 11. 1. Найти координаты точки М, лежащей на единичной окружности и соответствующей числу
- 12. 2. Дана точка М с абсциссой ½. Найдите ординату этой точки; укажите три угла поворота, в
- 13. 3. Дана точка М с абсциссой -½. Найдите ординату этой точки; укажите три угла поворота, в
- 14. Решите уравнение
- 15. Решите уравнение
- 16. π 0 arccos а Арккосинусом числа а называют такое число из промежутка [0;π ], косинус которого
- 17. Решим при помощи числовой окружности уравнение cos х = a. 1) Нет точек пересечения с окружностью.
- 18. Решим при помощи числовой окружности уравнение cos х = a. 2) cos х = 1 х
- 19. Решим при помощи числовой окружности уравнение cos х = a. 3) а = 0 Частное решение
- 20. Решим при помощи числовой окружности уравнение cos х = a. 4) Общее решение arccos а -arccos
- 21. Уравнение cos х = a называется простейшим тригонометрическим уравнением 0 x y 2. Отметить точку а
- 22. Уравнение cos t = a a) при -1 t1 = arсcos a + 2πk, k ϵ
- 23. Решите уравнение 1) cos х = 2) cos х = -
- 24. Решите уравнение 3) cos 4x = 1 4x = 2πn, n ϵ Z 4)
- 25. Решите уравнение 5) .
- 26. Уравнение sin t = a a) при -1 t1 = arсsin a + 2πn, n ϵ
- 27. Решите уравнение sin х = , , x = ( -1)k + πk, k ϵ Z
- 28. Решите уравнение 2) sin х = - x = ( -1)k+1 ; , , ; x
- 29. Задание 2. Найти корни уравнения: 1) a) sin x =1 б) sin x = - 1
- 30. Уравнение tg t = a при любом а ϵ R имеет одну серию решений х =
- 31. Решите уравнение 1) tg x = х = аrctg + πn, nϵ Z. x = +
- 32. Уравнение ctg t = a при любом а ϵ R имеет одну серию решений х =
- 33. Решите уравнение 1) ctg x = 1 х = аrcctg 1 + πn, nϵ Z, х
- 34. Подводим итоги
- 35. Продолжите фразу : Сегодня на уроке я повторил … Сегодня на уроке я узнал … Сегодня
- 37. Скачать презентацию

![С помощью тригонометрической окружности найти все значения из промежутка [-2π; 2π]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/716024/slide-2.jpg)


![«Верно - неверно». 1) sin2x+cos2x=1 – основное тригонометрическое тождество? 2) [-1;1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/716024/slide-5.jpg)





























 Программно-аппаратный комплекс для автоматизации управленческой деятельности школы
Программно-аппаратный комплекс для автоматизации управленческой деятельности школы Самый умный
Самый умный В мире песочных форм и фигур
В мире песочных форм и фигур Аттестационная работа. Рецензия на проектно-исследовательскую работу «Виртуальные и реальные маршруты Казани»
Аттестационная работа. Рецензия на проектно-исследовательскую работу «Виртуальные и реальные маршруты Казани» Единицы измерения площадей
Единицы измерения площадей Геометрические тела
Геометрические тела Тренажёр. Полёт бабочки. (1 класс)
Тренажёр. Полёт бабочки. (1 класс) Самый умный. Математическая игра
Самый умный. Математическая игра Преобразование выражений содержащих квадратные корни
Преобразование выражений содержащих квадратные корни Графические методы в С5
Графические методы в С5 «Ох уж эта математика» Урок в 5 классе
«Ох уж эта математика» Урок в 5 классе  Правильные многогранники. (11 класс)
Правильные многогранники. (11 класс) Множества. Комбинаторика
Множества. Комбинаторика Столбчатые диаграммы
Столбчатые диаграммы Весёлая математика. (ДОУ)
Весёлая математика. (ДОУ) Презентация по математике "Окружность" - скачать бесплатно
Презентация по математике "Окружность" - скачать бесплатно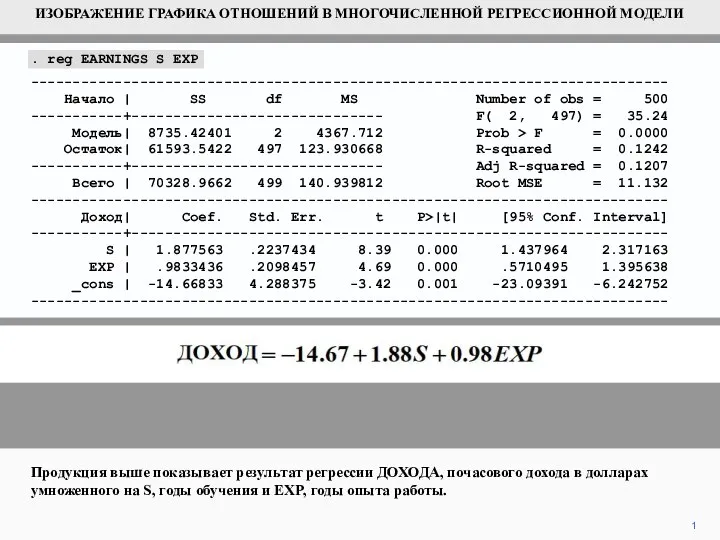 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели Показникові нерівності
Показникові нерівності Касательная к окружности
Касательная к окружности Решение задач с помощью уравнений (5 класс)
Решение задач с помощью уравнений (5 класс) Устный счет
Устный счет Тема: «КОНУС»
Тема: «КОНУС» Урок математики 1 класс
Урок математики 1 класс Эйлеровы графы. Пути и циклы Эйлера
Эйлеровы графы. Пути и циклы Эйлера Презентация по математике "Преобразование двойных радикалов" - скачать
Презентация по математике "Преобразование двойных радикалов" - скачать  Теорема Пифагора
Теорема Пифагора Площадь треугольника и подобие
Площадь треугольника и подобие Тригонометрические уравнения
Тригонометрические уравнения