Слайд 3

1. Уравнения, разрешаемые относительно y ′ неоднозначно
Пусть F(x, y, y ′) = 0 таково, что его
можно разрешить относи-
тельно y ′ неоднозначно.
Т.е. уравнение F(x, y, y ′) = 0 эквивалентно k различным уравнениям
y ′ = f1(x,y) , y ′ = f2(x,y) , y ′ = f3(x,y) , … , y ′ = fk(x,y) . (15)
Предположим, что для каждого из уравнений (15) найден общий интеграл:
Φ1(x , y , C) = 0 , Φ2(x , y , C) = 0 , …., Φk(x , y , C) = 0 . (16)
Совокупность общих интегралов (16) называется общим интегралом уравнения разрешаемого относительно y ′ не-
однозначно.









 Высота. Длина. Площадь
Высота. Длина. Площадь Площадь многоугольников. Решение задач
Площадь многоугольников. Решение задач Алгоритм перевода десятичной записи числа в запись в позиционной системе с заданным основанием
Алгоритм перевода десятичной записи числа в запись в позиционной системе с заданным основанием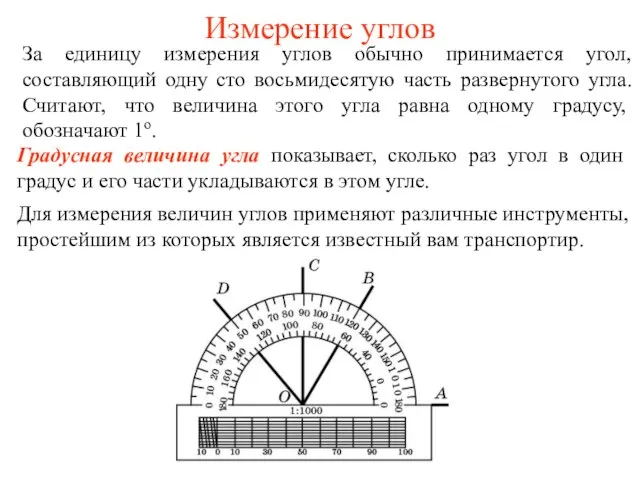 Измерение углов. Вопросы, упражнения
Измерение углов. Вопросы, упражнения Разложение разности квадратов на множители
Разложение разности квадратов на множители Решения задач
Решения задач Дискретні випадкові величини. Числові характеристики. Закони розподілу
Дискретні випадкові величини. Числові характеристики. Закони розподілу Буквенные выражения. Решение задач
Буквенные выражения. Решение задач Численные методы решения обыкновенных дифференциальных уравнений
Численные методы решения обыкновенных дифференциальных уравнений Умножение и деление чисел на 10
Умножение и деление чисел на 10 Умножение и деление дробей. Решение задач. 6 класс
Умножение и деление дробей. Решение задач. 6 класс Прямоугольник. Свойство противоположных сторон прямоугольника
Прямоугольник. Свойство противоположных сторон прямоугольника Презентация по математике "Решение уравнений 6 класс" - скачать
Презентация по математике "Решение уравнений 6 класс" - скачать  Вероятность события
Вероятность события Геометрическое истолкование производной
Геометрическое истолкование производной Вычисление дифиринциальных уравнений методом Адамса
Вычисление дифиринциальных уравнений методом Адамса Выполнила: Артюшевская Елена. г. Елец, Липецкая область, МОУ лицей № 5, 8 «Б» класс.
Выполнила: Артюшевская Елена. г. Елец, Липецкая область, МОУ лицей № 5, 8 «Б» класс. Понятие многогранника. Призма
Понятие многогранника. Призма Треугольник
Треугольник Үшбұрыштың ішкі бұрыштарының қосындысы
Үшбұрыштың ішкі бұрыштарының қосындысы Презентация по математике "Равновеликие и равносоставленные плоские фигуры" - скачать
Презентация по математике "Равновеликие и равносоставленные плоские фигуры" - скачать  Нахождение площади фигуры на клетчатой бумаге. Применение формул известных площадей
Нахождение площади фигуры на клетчатой бумаге. Применение формул известных площадей Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Отображение Пуанкаре
Отображение Пуанкаре Все об окружности
Все об окружности Найди ошибку. Дидактическая игра по геометрии (7 класс)
Найди ошибку. Дидактическая игра по геометрии (7 класс) Устные приёмы умножения и деления чисел в пределах 1000
Устные приёмы умножения и деления чисел в пределах 1000 Понятие графа. Решение задач
Понятие графа. Решение задач