Содержание
- 2. Основные понятия Математическая величина Скалярная величина (характеризуется численным значением) Векторная величина (Характеризуется численным значением и направлением)
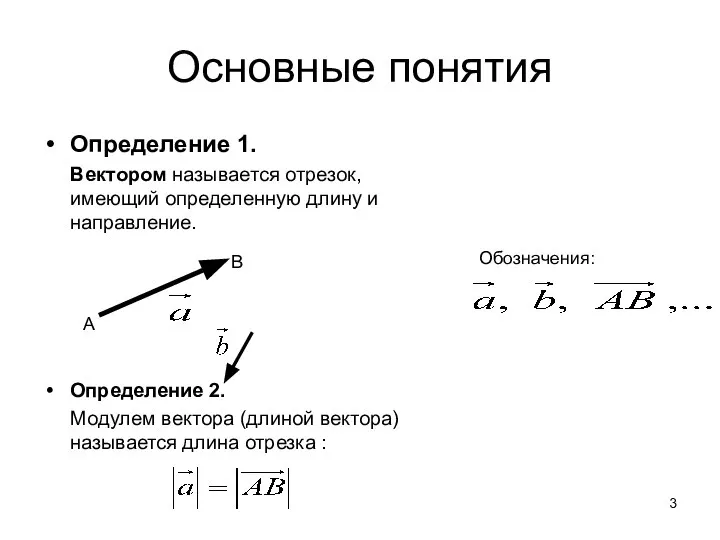
- 3. Основные понятия Определение 1. Вектором называется отрезок, имеющий определенную длину и направление. Определение 2. Модулем вектора
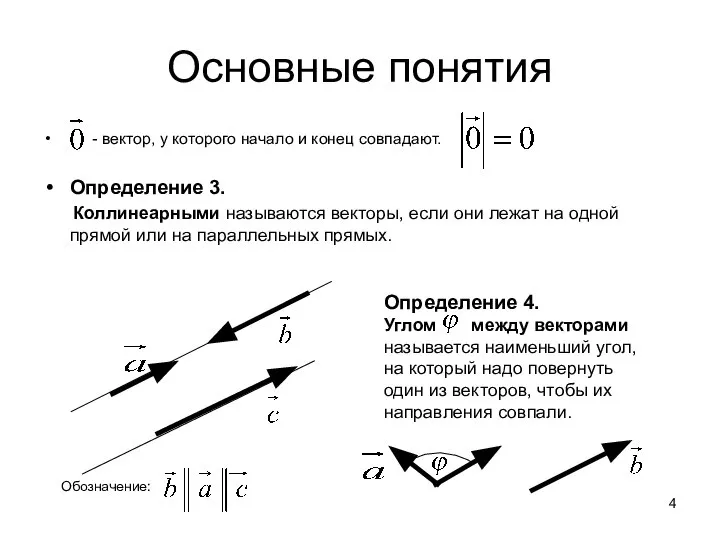
- 4. Основные понятия - вектор, у которого начало и конец совпадают. Определение 3. Коллинеарными называются векторы, если
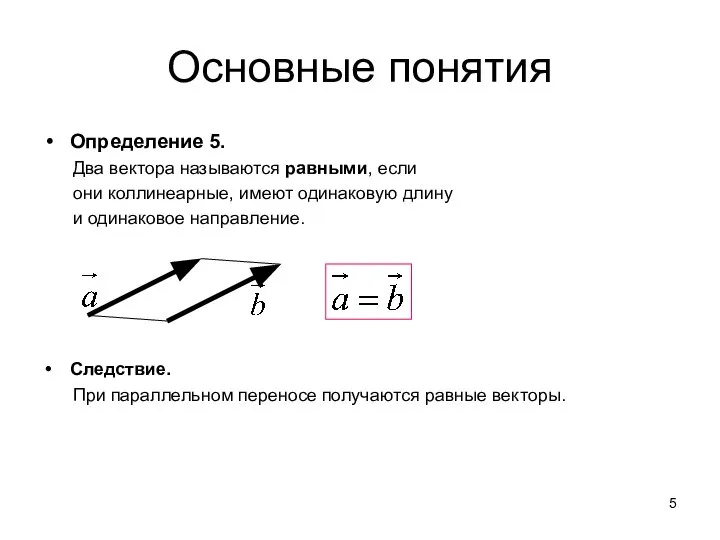
- 5. Основные понятия Определение 5. Два вектора называются равными, если они коллинеарные, имеют одинаковую длину и одинаковое
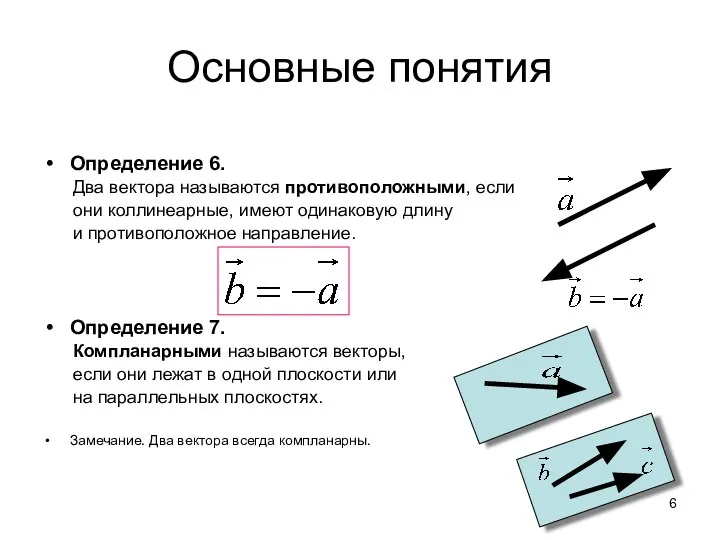
- 6. Основные понятия Определение 6. Два вектора называются противоположными, если они коллинеарные, имеют одинаковую длину и противоположное
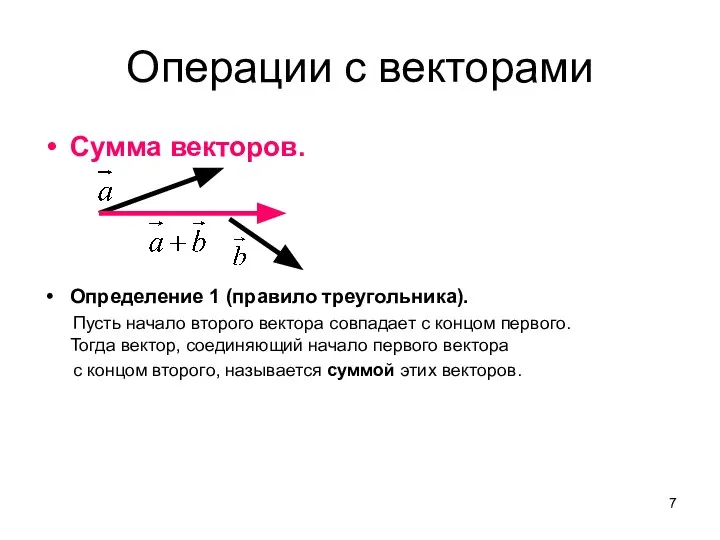
- 7. Операции с векторами Сумма векторов. Определение 1 (правило треугольника). Пусть начало второго вектора совпадает с концом
- 8. Операции с векторами Сумма векторов. Определение 2 (правило параллелограмма). Пусть начала первого и второго векторов совпадают.
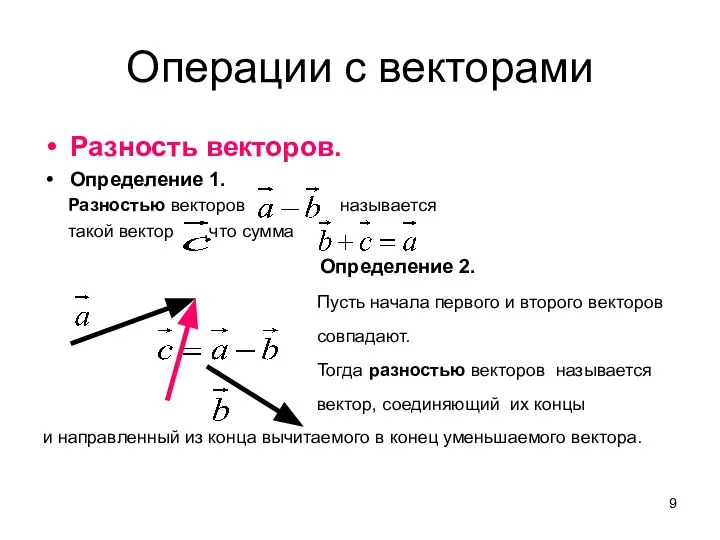
- 9. Операции с векторами Разность векторов. Определение 1. Разностью векторов называется такой вектор ,что сумма Определение 2.
- 10. Операции с векторами Произведение вектора на число. Определение. Произведением вектора на число называется вектор , коллинеарный
- 11. Операции с векторами Пример. Задан вектор . Построить векторы Построение : Теорема. Пусть . Векторы и
- 12. Разложение векторов Разложение векторов по ортам. Определение 1. Ортом вектора называется вектор , имеющий единичную длину
- 13. Разложение векторов Рассмотрим прямоугольную систему координат. Теорема 3. В пространстве любой вектор можно разложить по ортонормированному
- 14. Разложение векторов Определение 3. Коэффициенты x, y, z разложения называются прямоугольными координатами вектора : Частный случай.
- 15. Проекции вектора Рассмотрим вектор и ось Определение. Проекцией вектора на ось называется разность проекций конца и
- 16. Проекции вектора В пространстве: Следствие. Если вектор задан двумя точками, - начало, - конец, то
- 17. Действия с векторами в координатной форме Сумма и разность векторов, произведение вектора на число. Пусть Тогда
- 18. Действия с векторами в координатной форме Необходимое и достаточное условие коллинеарности векторов, заданных в координатной форме.
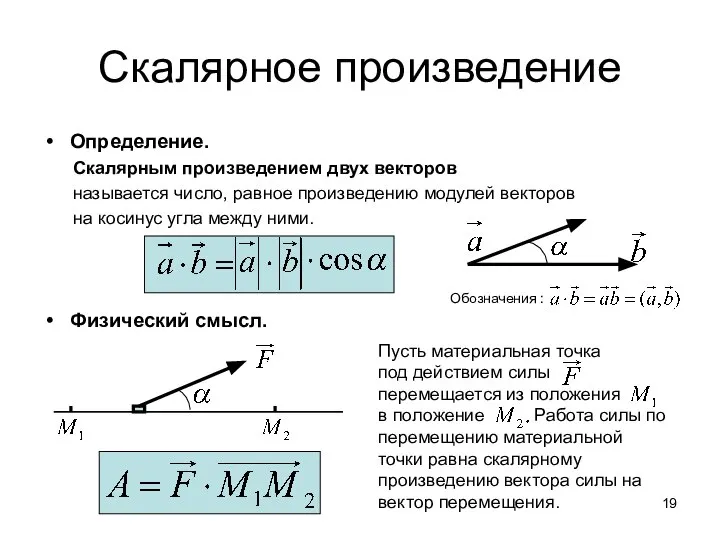
- 19. Скалярное произведение Определение. Скалярным произведением двух векторов называется число, равное произведению модулей векторов на косинус угла
- 20. Скалярное произведение Свойства скалярного произведения. 1. 2. 3. 4. Следствия из формулы 4 :
- 21. Скалярное произведение 5. 6. Скалярный квадрат вектора равен квадрату его модуля. 7. Необходимое и достаточное условие
- 22. Скалярное произведение Скалярное произведение векторов, заданных в координатной форме. Пусть Тогда Скалярное произведение векторов равно сумме
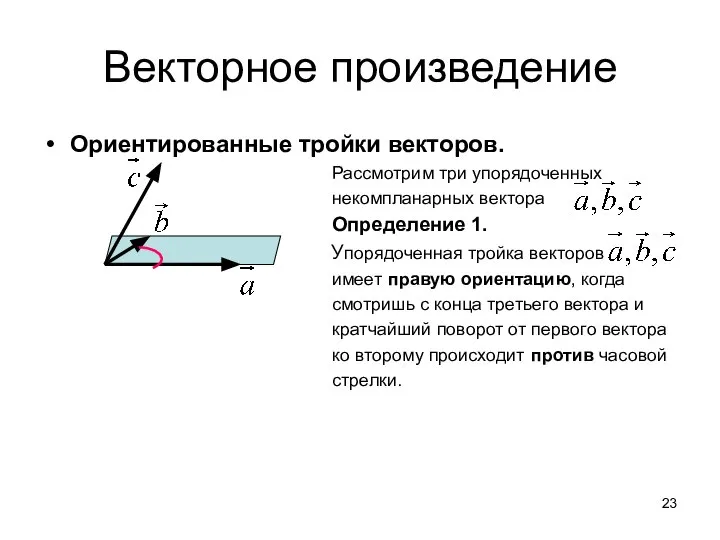
- 23. Векторное произведение Ориентированные тройки векторов. Рассмотрим три упорядоченных некомпланарных вектора Определение 1. Упорядоченная тройка векторов имеет
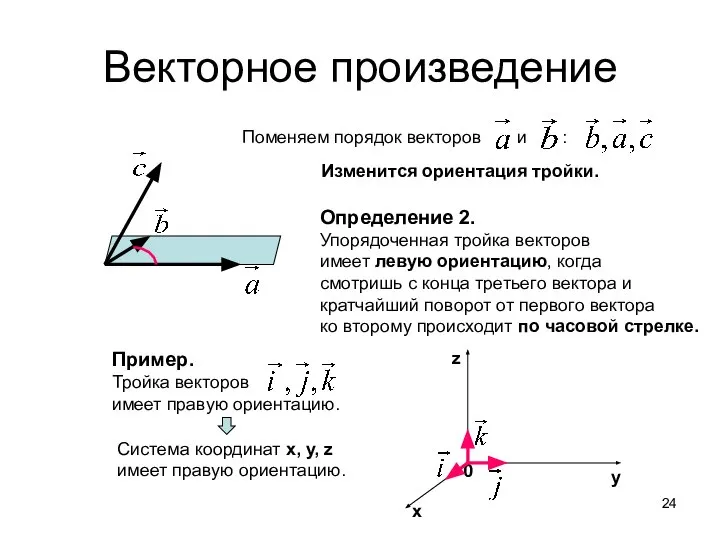
- 24. Векторное произведение Поменяем порядок векторов и : Изменится ориентация тройки. Определение 2. Упорядоченная тройка векторов имеет
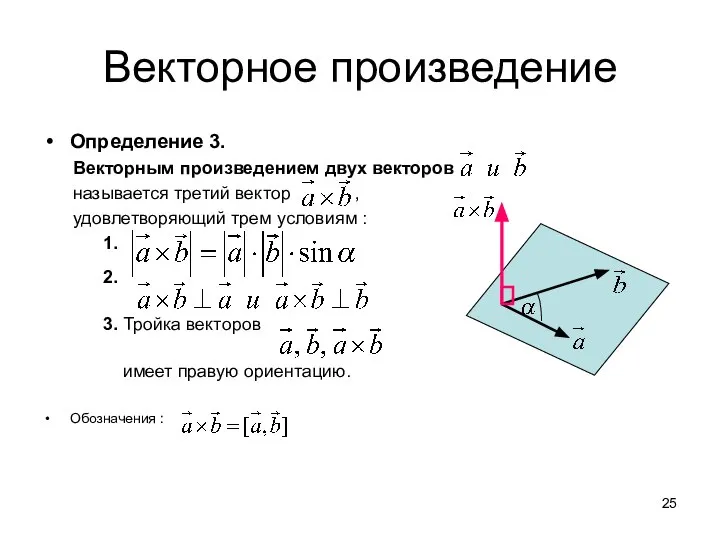
- 25. Векторное произведение Определение 3. Векторным произведением двух векторов называется третий вектор , удовлетворяющий трем условиям :
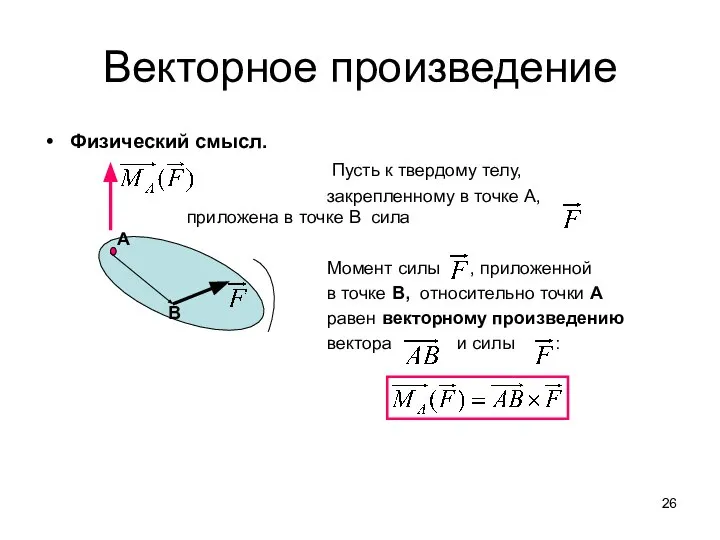
- 26. Векторное произведение Физический смысл. Пусть к твердому телу, закрепленному в точке А, приложена в точке В
- 27. Векторное произведение Свойства векторного произведения. 1. 2. 3. 4. Геометрический смысл . Модуль векторного произведения двух
- 28. Векторное произведение 5. Необходимое и достаточное условие коллинеарности двух векторов. Два ненулевых вектора коллинеарны тогда и
- 29. Векторное произведение Векторное произведение векторов, заданных в координатной форме. Пусть Тогда
- 30. Смешанное произведение Определение. Смешанным произведением трех векторов называется векторное произведение первых двух векторов, умноженное скалярно на
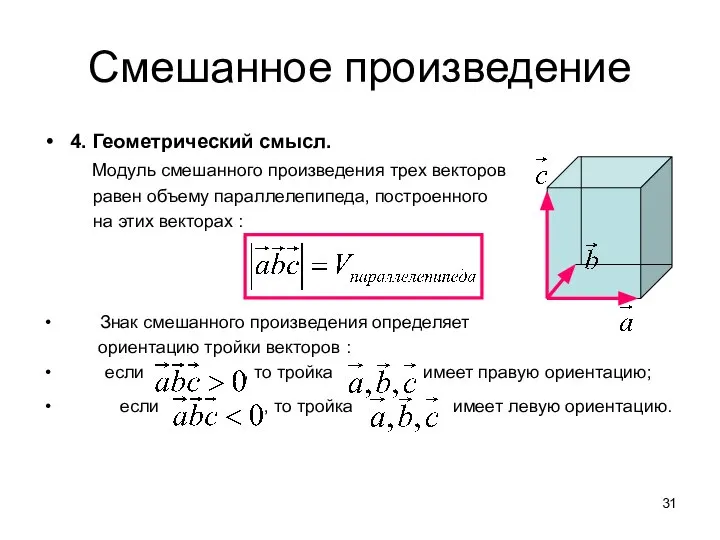
- 31. Смешанное произведение 4. Геометрический смысл. Модуль смешанного произведения трех векторов равен объему параллелепипеда, построенного на этих
- 33. Скачать презентацию

















 Текстовые задачи. Задание №1
Текстовые задачи. Задание №1 Презентация по математике "Вычитание" - скачать бесплатно
Презентация по математике "Вычитание" - скачать бесплатно Сложение натуральных чисел и его свойства. 5 класс
Сложение натуральных чисел и его свойства. 5 класс Решение уравнения cosx = a. Понятие арккосинуса числа
Решение уравнения cosx = a. Понятие арккосинуса числа Классификация систем нечеткой логики
Классификация систем нечеткой логики Площадь. Свойства площади. Формула площади прямоугольника
Площадь. Свойства площади. Формула площади прямоугольника Обобщение по 3-м формулам сокращенного умножения
Обобщение по 3-м формулам сокращенного умножения Сложение дробей с разными знаменателями. Законы сложения
Сложение дробей с разными знаменателями. Законы сложения Геометрический и физический смысл производной
Геометрический и физический смысл производной Перпендикуляр и наклонные. Угол между прямой и плоскостью
Перпендикуляр и наклонные. Угол между прямой и плоскостью Цилиндр, конус, шар
Цилиндр, конус, шар Демоверсия ГИА 2011 год Учитель ОУ СОШ №19 Лурда Л.Н.
Демоверсия ГИА 2011 год Учитель ОУ СОШ №19 Лурда Л.Н. Способы решения показательных уравнений
Способы решения показательных уравнений Эталоны единиц измерений
Эталоны единиц измерений Арифметические действия с десятичными дробями Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»
Арифметические действия с десятичными дробями Учитель математики Бадюк Ольга Ярославна, МКОУ «Москаленский лицей»  Төрле тамгалы саннар белән барлык гамәлләр
Төрле тамгалы саннар белән барлык гамәлләр Взаимное расположение прямых и плоскостей в пространстве
Взаимное расположение прямых и плоскостей в пространстве Устная нумерация чисел в пределах 1000
Устная нумерация чисел в пределах 1000 Синус, косинус и тангенс угла
Синус, косинус и тангенс угла Применение интеграла к решению физических задач
Применение интеграла к решению физических задач Прямоугольный треугольник
Прямоугольный треугольник Презентация по математике "Соревнование знатоков математики" - скачать бесплатно
Презентация по математике "Соревнование знатоков математики" - скачать бесплатно Презентация по математике "Сложение натуральных чисел и его свойства" - скачать
Презентация по математике "Сложение натуральных чисел и его свойства" - скачать  Решение систем нелинейных уравнений
Решение систем нелинейных уравнений Показательная и тригонометрические функции комплексного переменного
Показательная и тригонометрические функции комплексного переменного Презентация по математике "Комбинаторика" - скачать
Презентация по математике "Комбинаторика" - скачать  ЕГЭ профильная математика. Задание № 1. ЕГЭ базовая математика. Задание № 6
ЕГЭ профильная математика. Задание № 1. ЕГЭ базовая математика. Задание № 6 Методика изучения массы
Методика изучения массы