Содержание
- 2. Якщо функція f(x) неперервна на відрізку [a;b](де a Розбити цей відрізок на n частинних відрізків довжиною
- 3. Означення Якщо по різному ділити відрізок [a;b] на n частинних відрізків і по-різному вибирати на них
- 4. Властивості визначеного інтеграла 1) При перестановці меж інтегрування знак інтегралу змінюється на протилежний: 2) Інтеграл з
- 5. 5) Постійний множник k можна виносити за знак інтеграла: Для обчислення визначеного інтеграла використовується формула Ньютона-Лейбніца:
- 6. Приклад 1. Приклад 2.
- 7. 2. Метод заміни змінної у визначеному інтегралі. Якщо визначений інтеграл перетворюється за допомогою підстановки: в інший
- 8. Приклад 3.
- 9. Інтегрування частинами у визначеному інтегралі. Якщо підінтегральний вираз у визначеному інтегралі можна представити у вигляді добутку
- 10. Приклад 4.
- 11. 3. Невласні інтеграли. а) Інтеграли з нескінченними межами. Означення. Якщо існує скінченна границя: то цю границю
- 12. Тобто: (3) У цьому випадку кажуть, що інтеграл існує або він є збіжним. Якщо не має
- 13. Приклад. Обчислити інтеграл: Розв’язок:
- 14. б) Інтеграли від розривних функцій. Якщо функція визначена та неперервна у відкритому інтервалі: ,а у точці
- 15. Якщо функція f(x) має розрив у точці x = c всередині відрізка [a, b], то вважаємо,
- 16. 4. Обчислення площ плоских фігур. Площу криволінійної трапеції, що обмежена неперервною кривою , віссю Ох, та
- 17. Якщо плоска фігура обмежена двома неперервними кривими, рівняння яких: ,причому скрізь на відрізку , та двома
- 18. Економічні задачі, що зводяться до обчислення визначених інтегралів Якщо -продуктивність праці в момент часу t, то
- 19. Задача 1. Знайти обсяг продукції, виробленої за чотири роки, якщо продуктивність праці характеризується формулою: . Розв’язання.
- 20. Знаходження середнього часу, затраченого на виготовлення виробу Нехай відома функція ,що описує зміни витрат часу t
- 22. Скачать презентацию

![Означення Якщо по різному ділити відрізок [a;b] на n частинних відрізків](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/658136/slide-2.jpg)


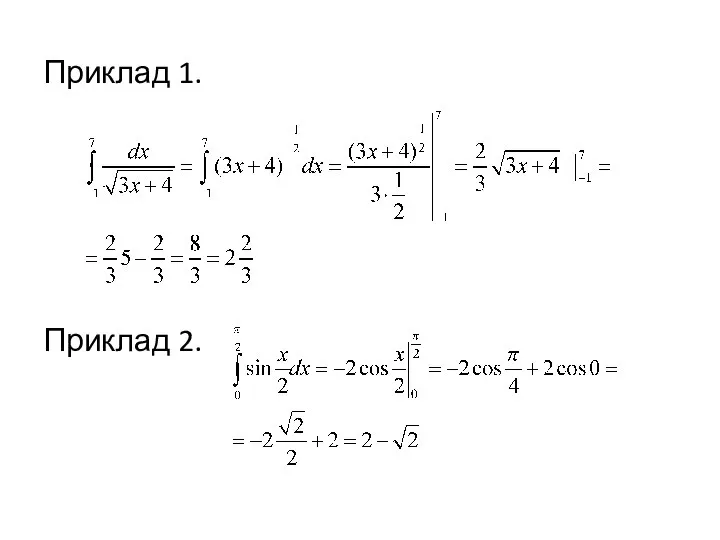

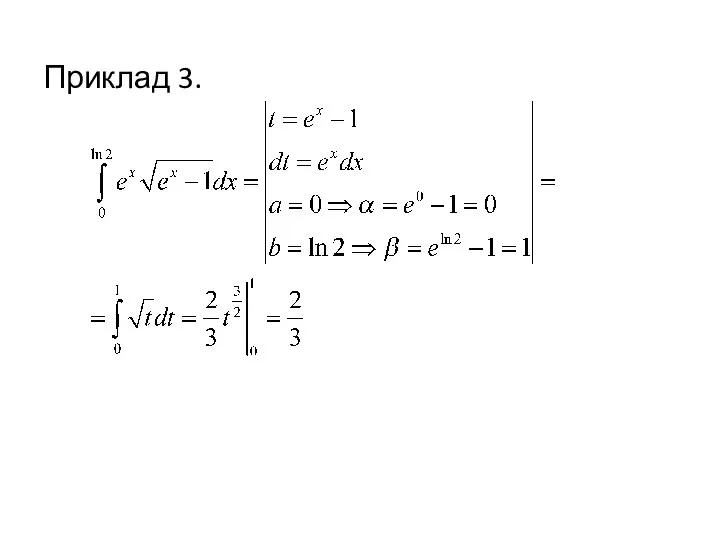












 Оценка точности функций
Оценка точности функций Нахождение части от целого
Нахождение части от целого Открытый банк заданий по математике. Задача №13
Открытый банк заданий по математике. Задача №13 Презентация для класса Неполные квадратные уравнения
Презентация для класса Неполные квадратные уравнения  «Своя игра». Внеклассное мероприятие по математике
«Своя игра». Внеклассное мероприятие по математике Вставляем пропущенное число с дракончиками. Урок математики
Вставляем пропущенное число с дракончиками. Урок математики Скрещивающиеся прямые
Скрещивающиеся прямые Исследовательские задачи на уроках математики
Исследовательские задачи на уроках математики Тела вращения
Тела вращения Реальная математика
Реальная математика Цифры от 0 до 9. УМК «Планета знаний»
Цифры от 0 до 9. УМК «Планета знаний» Квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда
Квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда Умножение и деление круглых чисел
Умножение и деление круглых чисел Алгебраическая дробь. Сокращение дробей
Алгебраическая дробь. Сокращение дробей Состав числа
Состав числа Численные методы решения нелинейных уравнений и систем нелинейных уравнений
Численные методы решения нелинейных уравнений и систем нелинейных уравнений Связи между двумя переменными (лекция 9)
Связи между двумя переменными (лекция 9) Презентация по математике "Особенности геометрических построений на компьютере" - скачать
Презентация по математике "Особенности геометрических построений на компьютере" - скачать  Модели организации строительного процесса, их математическое и графическое отображение
Модели организации строительного процесса, их математическое и графическое отображение Сечения тетраэдра
Сечения тетраэдра Объем прямой призмы
Объем прямой призмы Фракталы вокруг нас
Фракталы вокруг нас  Игра. Математический бой
Игра. Математический бой Интеллектуальная игра: «Морской бой»
Интеллектуальная игра: «Морской бой» Решение задач по теме «Четырёхугольники»
Решение задач по теме «Четырёхугольники» Простейшие тригонометрические уравнения. Задания для устного счета
Простейшие тригонометрические уравнения. Задания для устного счета Набор инсулина в шприц
Набор инсулина в шприц Счет в пределах 20. Подготовка к введению задач в два действия
Счет в пределах 20. Подготовка к введению задач в два действия